 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Этапы синтеза комбинационной схемы
Этап 1. Наиболее часто встречающийся на практике способ задания схемы – это объяснение ее работы на понятийном уровне в виде набора фраз обычного языка (например, русского). Сложность этапа связана с тем, что задание описывается неформальными терминами, допускающими неоднозначную трактовку. Основная цель этапа – формализация задания, в процессе которой определяются количество входных логических переменных (аргументов) и значения выходной переменной (функции) для каждой комбинации значений аргументов. Результат этапа – таблица истинности. О уже задание, неоднозначное толкование которого невозможно. Наиболее трудно обнаруживаемые ошибки возникают именно на этапе формализации. Этап 2. Если функция определена не на всех наборах аргументов, то нужно ликвидировать неоднозначность таблицы. Этап 3. Составить СДНФ для нескольких вариантов доопределения. Этап 4. Минимизировать СДНФ любым доступным методом. Этап 5. Реализовать получившиеся ДНФ на заданном логическом базисе. Для сравнения между собой различных вариантов схем, реализующих одну и ту же функцию, нужно уметь как-то оценивать их качество. Наиболее распространена оценка схемы по двум параметрам – задержке - Т и аппаратурным затратам - W. . Подсчёт W удобно производить в двенадцатых долях корпуса : 12 - это число логических выводов корпуса наименьшего размера. Пример. На логических микросхемах серии К155 (табл. 2.1) построить несколько вариантов схем, реализующих заданную минимальную ДНФ Схемная реализация в базисе НЕ, И, ИЛИ показана на рис.2.3,а. Аппаратурные затраты состоят из четырёх инверторов- (ЛН1), каждый из которых занимает 1/6 корпуса, двух элементов 2И- (ЛА3) и двух элементов 2ИЛИ- (ЛЛ1), каждый из которых занимает 1/4 корпуса. Считая, что задержки всех элементов одинаковы получим: Т=4t. W=4*1/6+2*1/4+2*1/4=20/12. Неиспользованные элементы частично занятых корпусов не учитываются, поскольку они могут быть использованы в других узлах.11 Реализация Q с использованием микросхем ЛР3 показана на рис. 3.1,б. Для неё нужно пять инверторов ЛН1 и целиком микросхему ЛР3 : Т=3t; W=5*1/6+1=22/12 корпуса. Затраты W немного возросли, а задержка уменьшилась до 3t. Применив к функции Q правило де Моргана, получим
Можно попытаться использовать формулы де Моргана для уменьшения числа входных инверторов. Тогда Ещё одно применение формулы де Моргана даёт Если в последнем выражении раскрыть скобки, то получим ещё один вариант схемы Отметим, что хотя за основу была взята минимальная ДНФ, её схемная реализация оказалась самой неэкономичной из всех. Противоречия здесь нет. Минимальная ДНФ минимальна лишь в определённом смысле: это выражение, имеющее минимальное суммарное число букв. Переводя на язык аппаратуры, можно сказать, что это соответствует минимуму суммы входов всех конъюнкторов, реализующих элементарные конъюнкции ДНФ в трехъярусной схеме НЕ-И-ИЛИ типа показанной на рис.3.1,а. Затраты инверторов и дизъюнкторов этот критерий игнорирует. Отсюда не следует, что минимизация не нужна вообще: чем компактнее выражение, тем легче обрабатывать его дальше.
Рис. 2.3,а. Варианты реализации функции Y.
Несколько полезных рекомендаций: -сократить число инверторов, применив формулу де Моргана; -использовать элементы И-ИЛИ-НЕ - они логически мощнее, чем И‑НЕ, ИЛИ‑НЕ; -подбирать такие элементы, чтобы по возможности использовались все их входы; -если выражение плохо минимизируется, попытаться применить элементы М2; -вместо прямой функции реализовать её инверсию. Алгоритма, который позволял бы целенаправленно строить хорошие схемы, в общем случае не существует. Не существует и чётких признаков окончания поиска хорошей схемы. В этом смысле разобранный пример не следует воспринимать как требование всегда проводить такую тщательную обработку любого выражения. Это просто иллюстрация характера работы при логическом проектирования. То же самое можно сказать и о процессе построения более сложных блоков из микросхем средней и большой интеграции. Слабо алгоритмизированный, поисковый, изобретательный стиль работы характерен для всех этапов функционально-логического проектирования цифровых устройств.
Поиск по сайту: |
 Сравнить полученные результаты.
Сравнить полученные результаты.
 (рис.3.1,в), Т=3t; W=3*1/6+2*1/4+1*1/3=16/12 корпуса. Схема оказалась заметно экономичнее при том же быстродействии.
(рис.3.1,в), Т=3t; W=3*1/6+2*1/4+1*1/3=16/12 корпуса. Схема оказалась заметно экономичнее при том же быстродействии.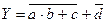 (рис.2.3,г), Т=2t; W = 11/12 корпуса. Удалось выиграть и в быстродействии и в оборудовании.
(рис.2.3,г), Т=2t; W = 11/12 корпуса. Удалось выиграть и в быстродействии и в оборудовании. (рис.2.3,д) Т=3t ; W=9/12 корпуса. Схема хотя и более медленная, но очень экономичная.
(рис.2.3,д) Т=3t ; W=9/12 корпуса. Схема хотя и более медленная, но очень экономичная. (рис.2.3,е), Т=t; W=12/12 корпуса. Задержка этой схемы оказалась наименьшей из всех рассмотренных.
(рис.2.3,е), Т=t; W=12/12 корпуса. Задержка этой схемы оказалась наименьшей из всех рассмотренных.