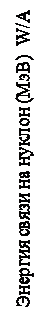|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Преобразования Лоренца и «парадоксы» релятивистской кинематики
Восстановив в правах принцип относительности и постулировав постоянство скорости света во всех ИСО, Эйнштейн показал, что несоответствие уравнений Максвелла принципу относительности связано с «некорректностью» применения преобразований Галилея и что на самом деле переход от координат и времени одной ИСО к координатам и времени другой ИСО необходимо производить, используя другие формулы. Эти формулы называются преобразованиями Лоренца. Для частного случая, когда К¢-система отсчета перемещается с постоянной скоростью V вдоль оси x К-системы отсчета, они имеют следующий вид
где с - по-прежнему скорость света. Уравнения Максвелла оказываются инвариантными относительно преобразований Лоренца, что полностью устраняет все противоречия классической электродинамики с принципом относительности. В то же время, легко видеть, что старые преобразования Галилея являются частным случаем преобразований Лоренца, соответствующим условию V<< c, т.е. движению объектов с малыми (по сравнению с с) скоростями. Следствием преобразований Лоренца являются несколько выводов, которые, на первый взгляд, носят “парадоксальный” характер, но которые, тем не менее, совершенно реальны и неоднократно выдерживали опытную проверку.
1. «Сокращение» длины движущихся объектов. Представим себе неподвижную линейку длиной L0. Эта длина называется собственной длиной линейки, а система отсчета, в которой линейка неподвижна, - собственной системой отсчета, которую мы в дальнейшем будем обозначать К0. Если линейка движется со скоростью V относительно другой системы отсчета (К), то для наблюдателя в этой системе отсчета линейка будет казаться короче, так что ее длина L может быть вычислена по формуле:
L = L0
Следует отметить, что такое «сокращение» длины не связано с какими-то деформациями самой линейки, оно обусловлено тем, что одновременная фиксация концов движущейся линейки наблюдателем, находящимся в К-системе отсчета, является неодновременной в другой, в частности, в собственной системе отсчета. В результате, например, из К0-системы отсчета кажется, что сначала фиксируется положение правого конца линейки, а через некоторое время, когда линейка сместится на некоторое расстояние, фиксируется положение левого конца. Поэтому расстояние между этими засечками оказывается меньше, чем L0. Но, увы, наблюдатель в К-системе отсчета справедливо считает, что он фиксирует концы линейки одновременно, и заставить его измерять длину иначе нельзя. Этим и объясняется парадокс «сокращения» длины. Обратим внимание также на то, что поперечные размеры движущихся тел не изменяются по сравнению с неподвижными. Но ведь то, что касается концов линейки, в полной мере относится и к любым точкам пространства, даже если никаких линеек в нем нет. Поэтому можно сказать, что пространство имеет разную метрику в разных ИСО.
2. «Замедление» хода движущихся часов. Чтобы убедиться в том, что время в движущейся системе отсчета течет медленнее, чем в неподвижной, рассмотрим специальный вид часов2. Пусть эти часы представляют собой два неподвижных (К0-система отсчета) параллельных зеркала, расположенных на расстоянии L0 друг от друга, между которыми «бегает» световой “зайчик” (рис. 6.2). Время, за которое этот «зайчик» пробегает туда и обратно, очевидно, равно t0 = 2L0/с, где с - скорость света.
Неподвижные часы Движущиеся часы
Рис. 5.2. Релятивистский эффект замедления времени в движущейся системе отсчета
Пусть теперь эти часы движутся со скоростью V, например, направо. Наблюдатель, находящийся в неподвижной К-системе отсчета, видит, что «зайчик» проходит более длинный путь между зеркалами, так как L =
где t - время, за которое «зайчик» пробегает зигзагообразный путь в К-системе отсчета. Так как
то, решив это уравнение относительно t, получаем:
t =
Таким образом, интервал времени t между двумя событиями в К-системе отсчета оказывается больше, чем интервал времени t0 между теми же событиями в К0-системе отсчета. Поэтому и говорят, что движущиеся часы идут медленнее неподвижных. И здесь надо отметить, что указанное замедление относится не только к часам специального вида, но и ко всем движущимся объектам. В частности, даже процессы старения живых организмов замедляются, если эти организмы движутся. Из двух близнецов тот, который отправляется в космическое путешествие (назовем его А), стареет медленнее, чем его брат (В), остающийся на Земле. С этим примером связан знаменитый «парадокс близнецов», который заключается в следующем. Если близнец А через какое-то время вернется на Землю, то он должен увидеть своего брата В заметно постаревшим (предполагается, конечно, что близнец А перемещался с околосветовой cкоростью). Это следует из того, что А двигался, а В оставался неподвижным, т.е. с точки зрения близнеца В. Но ведь можно встать на точку зрения близнеца А, который считает себя неподвижным и относительно которого его брат В сначала удалялся, а потом вернулся. И тогда следует считать, что А постареет больше, чем В. Таким образом, мы приходим к двум взаимоисключающим друг друга выводам. А разрешение «парадокса близнецов» связано с тем, что его участники, близнецы А и В, находились в несимметричных условиях. Чтобы вернуться на Землю, близнец А должен был изменить свою скорость на противоположную, т.е. какое-то время находиться в неинерциальной системе отсчета, для которой выводы СТО неприменимы. В то же время близнец В все время находился в ИСО. С учетом этого, именно А окажется моложе, чем В. 3. Релятивистский закон преобразования скоростей. Из школьного курса физики хорошо известна формула преобразования скоростей при переходе из одной (К) ИСО в другую (К¢):
v = v¢ + V (5.8)
где V -скорость К¢-системы отсчета относительно К-системы отсчета. Чтобы получить эту формулу достаточно продифференцировать по времени соотношение r = r¢ + Vt. В релятивистской кинематике указанная формула не имеет места, а преобразования скоростей производятся по более сложным формулам, согласованным с преобразованиями Лоренца. В частности, x-проекции скоростей преобразуются в соответствии со следующим выражением:
vx=
где предполагается, что К¢-система отсчета движется с постоянной скоростью V вдоль оси x относительно К-системы отсчета. Пусть v¢x = с, тогда по формуле Галилея мы бы имели vx = с + V > c, что невозможно. В то же время по приведенной выше релятивистской формуле получается
так что скорость света оказывается инвариантной (не изменяется) при переходе из одной ИСО в другую.
5. 7. Релятивистская динамика и взаимосвязь массы и энергии
Еще более радикальные изменения произошли в релятивистской динамике. Прежде всего, ньютоновское понятие массы как не зависящей от скорости характеристики инерционных свойств материальных объектов становится как минимум «бесполезным». В частности, для таких «масс» нельзя записать закон сохранения импульса, справедливость которого ни у кого не вызывает сомнения. Ведь в противном случае придется допустить, что тела могут произвольно, без всяких внешних причин начать двигаться. Чтобы «спасти» закон сохранения импульса, необходимо считать массу тела m зависящей от его скорости v:
m = где m0 - масса неподвижного тела (масса покоя), с - скорость света. Из приведенной формулы следует, что при увеличении скорости тела v его масса m возрастает, а при v Однако, пожалуй, самым существенным выводом СТО, непосредственно повлиявшим на научно-технический прогресс, стал вывод о взаимосвязи массы и энергии. В релятивистской динамике кинетическая энергия Т тела массы m0 не равна m0v2/2, а определяется разностью значений полной релятивистской энергии:
Е =
и так называемой энергии покоя:
E0 = m0c2 . (5.13)
Кстати, легко показать, что при v << c T @ m0v2/2, так что известная из школьного курса физики формула для кинетической энергии сохраняет свое значение для небольших скоростей движения тел. В то же время релятивистский подход к вопросу об энергии тела резко отличается от классического. В соответствии с СТО даже неподвижное тело массы m0, не находящееся в каких-либо внешних силовых полях, обладает энергией покоя E0 = m0c2. Эту энергию можно трактовать как «внутреннюю» энергию тела массы m0, даже если внутренняя структура этого тела не конкретизируется. Однако, в случае составного тела, например, атомного ядра, состоящего из нескольких нуклонов (нейтронов и протонов), физический смысл энергии покоя проясняется. Дело в том, что при сближении нуклонов и возникновении устойчивой связи между ними их энергия уменьшается на некоторую величину Есв, которая называется энергией связи. Это следует хотя бы из того, что для разрыва этой связи нужно затратить энергию Есв. Таким образом, энергия связанных нуклонов или, другими словами, энергия ядра En меньше, чем суммарная энергия образующих это ядро свободных нуклонов Е: En = E - Есв. В свою очередь, это приводит к тому, что масса ядра Mn становится меньше суммарной массы составляющих это ядро свободных нуклонов М на величину D = Есв/c2, которая в ядерной физике называется дефектом массы ядра. Зависимость удельной энергии связи Есв/A, где А - число нуклонов в ядре, от А приведена на рис. 5.3. Самым замечательным в этой зависимости является то, что она имеет максимум при А ~ 60. Это значит, что ядра с таким числом нуклонов являются наиболее устойчивыми, стабильными. В частности, к таким ядрам относится железо с А = 56.
Рис.5.3. Зависимость удельной энергии связи в ядре от его массового числа
Чтобы из таких ядер получить другие, с большим или меньшим числом нуклонов, надо затратить энергию, часто весьма значительную. А вот деление тяжелых ядер (А > 60) и синтез легких ядер (А < 60) приводят к появлению более устойчивых ядер и сопровождаются выделением энергии. Именно последовательный синтез ядер водорода и других легких элементов лежит в основе термоядерных процессов в звездах, поддерживая огромную температуру в их недрах на протяжении миллиардов лет. Такие же неуправляемые термоядерные процессы происходят в водородной бомбе. К сожалению, создать управляемую термоядерную реакцию, которая позволила бы практически полностью решить энергетическую проблему человечества, до сих пор не удалось. Современная ядерная энергетика основана на реакции деления тяжелых ядер урана.
Поиск по сайту: |

 x¢ =
x¢ =  ; y¢ = y; z¢ = z; t¢ =
; y¢ = y; z¢ = z; t¢ =  ; (5.3)
; (5.3) . (5.4.)
. (5.4.)

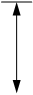
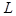
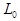





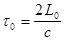
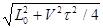 (5.6)
(5.6) t = 2L/c = (2/c)
t = 2L/c = (2/c) 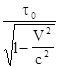 (5.7)
(5.7)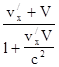 , (5.9)
, (5.9)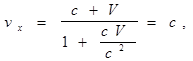 (5.10)
(5.10)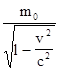 , (5.11)
, (5.11) c m
c m  (5.12)
(5.12)