|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическая модель олигополии
На практике рыночной властью, т.е. властью над ценообразованием, обладают не только фирмы, являющиеся чистыми монополистами. Во многих отраслях экономики конкурирует небольшое число фирм, каждая из которых обладает некоторой рыночной властью. Таковы, например, крупные металлургические комбинаты России (КМК, Запсиб, Магнитка и др.). Изучим рыночные механизмы в условиях олигополии, т.е. когда на рынке товара конкурирует небольшое число фирм. Рыночная власть и прибыль олигополистов частично зависят от того, как они взаимодействуют между собой. В некоторых олигопольных отраслях фирмы агрессивно конкурируют, а в других сотрудничают. Естественно, конкуренция приводит к снижению цен а, имея тенденцию к сотрудничеству, фирмы могут назначить цены выше предельных издержек и получить большую прибыль. Крайнюю форму сотрудничества представляет собой картель. На картельном рынке некоторые или все фирмы вступают в сговор по поводу захвата рынка. Определяя сообща цены товара и объемы продаж, они максимизируют свои прибыли. Картель отличается от монополии тем, что не может контролировать весь рынок товара по причине наличия фирм, не входящих в картель. Другая причина отличия - в нестабильности картеля как структуры, состоящей из фирм, преследующих каждая свои интересы. Олигополия является преобладающей формой современной рыночной структуры. На олигопольных рынках несколько фирм производят всю или почти всю продукцию. Чем шире олигополия, тем сложнее принятие экономических решений для фирм. Поэтому они могут предпринять стратегические усилия, чтобы затруднить вступление на рынок новых фирм. Олигополист принимает решение по установлению цены и объема выпускаемой им продукции. Экономическое решение олигополиста складывается сложнее, чем монополиста, так как имеет место конкуренция между несколькими фирмами. Поэтому фирма должна тщательно взвесить свои решения с точки зрения реакции соперников. Стратегические соображения должны быть глубокими и всесторонними. Каждая фирма учитывает реакцию конкурентов, зная, что те, в свою очередь, тоже будут взвешивать ее реакцию на их собственные решения. При этом фирма должна принимать во внимание возможность восстановления ее стратегических рассуждений конкурентами, и потому она должна поставить себя на место конкурентов и поразмыслить, какова бы была их реакция. Именно с позиций такой рекомендации разрабатываются принципы оптимального поведения олигополистов. Некоторые из них будут рассмотрены ниже. В этом параграфе рассмотрим моделирование задачи олигополиста и олигопольного рынка в целом. Определяющим свойством олигопольного рынка является то, что все конкурирующие фирмы могут влиять на цены продукции и затрат. Следовательно, прибыль каждой фирмы зависит и от экономических решений всех остальных фирм. Каково будет в этих условиях оптимальное решение олигополиста по объему выпуска и цене товара? Для получения ответа на этот вопрос необходимо построить математическую модель олигополиста и решить совместно систему, состоящую из задач всех конкурирующих между собой фирм. Обозначим через Согласно описания олигополии, цена товара
При возрастании выпусков цены понизятся. Поэтому
Аналогично, если фирмы увеличат покупки производственных факторов, произойдет повышение их цен. Поэтому
Пусть
Так как все олигополисты действуют на рынках одних и тех же товаров, то
Задача i-го олигополиста формулируется следующим образом:
при ограничениях (7.2.1)
Здесь Из вида целевой функции задачи (7.2.1) приходим к выводу, что максимизация прибыли Модель олигополии в целом имеет вид:
при ограничениях (7.2.2)
Такого рода модели называются конфликтными задачами принятия решения или играми n лиц. Конфликтный характер принятия решения здесь заключается в том, что каждая целевая функция Определение 7.1. Обозначим
Здесь Смысл оптимальности экономического решения Рассматривая отдельно задачу i-го олигополиста (7.2.1), составим для нее функцию Лагранжа
и выпишем необходимые условия оптимальности первого порядка (частные производные от функции Лагранжа берутся только по тем переменным, по которым максимизируется функция
Исключая из этой системы множитель Лагранжа
Следовательно, для вычисления оптимальных стратегий всех олигополистов в модели (7.2.2) будем иметь
участвующие в необходимых условиях (7.2.3), оценивают реакцию олигополистов на выпуск и затраты, осуществляемые друг другом. Поэтому эти величины называются предположительными вариациями. Относительно знаков частных производных (7.2.4) можно сделать различные предположения, каждое из которых ведет к различной методике анализа олигополии. Рассмотрим два таких подхода в более простом частном случае олигополии, называемом дуополией.
Анализ дуополии Курно Предположим, что имеется всего две конкурирующих по выпуску одного и того же товара фирмы. Это есть частный случай олигополии, называемый дуополией. Обе фирмы принимают решения по объему выпуска одновременно и тайно друг от друга, и конечная цена товара зависит от совокупного объема производства этих фирм. То есть, как и в олигополии, дуополисты имеют частичную рыночную власть (частичное влияние на цену товара). Модель дуополии впервые рассматривал французский экономист О. Курно еще в тридцатых годах прошлого столетия. Подход Курно основывается на гипотезе о том, что свое экономическое решение каждая фирма принимает в предположении о постоянном объеме производства своего конкурента. Другими словами, дуополист считает, что конкурент не реагирует на его выпуск. Чтобы лучше понять, как это происходит, рассмотрим пример. Предварительно заметим, что в дуополии фирма ориентируется на ту часть рыночного спроса, которая не обеспечена предложением другой фирмы. Поэтому для фирмы очень важно правильно оценить спрос населения на ее товар и объем производства конкурента. Пример 7.1. Пусть в дуополии фирмы имеют постоянные предельные издержки, а спрос и предельный доход описываются линейными функциями (имеют графиками прямые линии). Определить максимизирующие прибыли фирм объемы их производства, т.е. найти оптимальные выпуски фирм-дуополистов, при субъективном мнении каждой фирмы о постоянстве объема выпуска конкурента.
Рис. 7.3 Выбор объёма производства фирмы 1.
Для удобства назовем дуополистов фирмой 1 и фирмой 2. По условию примера фирма 1 считает, что фирма 2 определяет объем своего выпуска самостоятельно, не обращая внимания на объем производства фирмы 1. Поэтому фирма 1 будет строить свою стратегию, исходя из того или иного предположения о постоянном объеме производства фирмы 2. Определим максимизирующие прибыль фирмы 1 объемы производства при ее предположениях о производстве фирмы 2, равных соответственно Проведем линию постоянных предельных издержек фирмы 1 (на рис. 7.3 обозначена Пусть фирма 1 считает, что Пусть теперь фирма 1 считает, что Наконец, в предположении В зависимости от объема выпуска фирмы 2 получили последовательность
Рис. 7.4 Кривые реакции в дуополии
Точка пересечения Перейдем от графических построений для частного примера к общим аналитическим построениям. Математическую модель дуополии получим как частный случай задачи (7.2.2) при
при ограничениях (7.3.1)
где
Как и в олигополии,
Для вычисления оптимальных выпусков дуополистов имеется
где
- предположительные вариации дуополиста Определение 7.2. Модель (7.3.1) называется дуополией Курно, если в (7.3.2) выполнены условия
Как видно из определения, в дуополии Курно каждая фирма считает, что изменения объема ее собственного выпуска не повлияют на решение конкурента. Определение 7.3. Тройка По определению равновесие Курно должно одновременно удовлетворять условиям (7.3.2) и (7.3.3). Поэтому из (7.3.2) получаем
где
кажутся вполне логичными. При этих условиях равенство (7.3.4) принимает вид:
Сумма в левой части этого равенства есть предельные издержки j-го вида затрат для i-го дуополиста в состоянии равновесия Курно. Обозначим их через
Тогда из условия (7.3.6) для i-го дуополиста получаем равенство
при всех
Следовательно, в состоянии равновесия Курно предельные доходы дуополистов, умноженные на предельные выпуски, равны их предельным издержкам и их общее значение (7.3.7) есть оптимальная цена товара, соответствующая оптимальным предложениям Равенство (7.3.7) является аналитическим обоснованием того, что равновесие Курно получается в пересечении кривых реакций дуополистов (см. рис. 7.4). Замечание. Условие (7.3.5) практически может быть нарушено при дефицитности фактора j и когда обе фирмы пользуются услугами одного и того же рынка факторов производства. Пример 7.2. Вычислить равновесие Курно в дуополии, цена товара в которой определяется через выпуски по формуле В этом примере функция прибыли имеет вид
Необходимые условия оптимальности (7.3.2) запишутся в виде
Отсюда получаем систему для вычисления равновесия Курно:
Вычитая из первого уравнения второе, получаем
Откуда
Подставляя эти значения в формулу цены, получаем
Следовательно, в рассматриваемом примере состояние равновесия Курно есть
Кривые реакции дуополистов найдем из (7.3.10):
Рис. 7.5 Иллюстрация к примеру 7.2
В пересечении этих линий находится точка Полученный результат можно обобщить для олигополии с произвольным конечным числом (n) фирм. Как следует из (7.3.11), в этом случае равновесие Курно есть
Очевидно, что
Следовательно, в пределе (при Рассмотрим теперь поведение дуополистов Курно во временном аспекте. Как и прежде, моменты времени будем обозначать через
Из (7.3.10) с учетом временного лага можно получить два рекуррентных уравнения
описывающих динамику реакции дуополистов на выпуски друг друга. Решая эти уравнения, найдем две последовательности (кривые реакции)
первая из которых начинается в момент
Рис.7.6 Таблица последовательности выпусков
Рис. 7.7 Сходимость выпусков к равновесию Курно
Как следует из рис. 7.7, при возрастании Построенный динамический процесс отражает фактическое поведение фирм - изменение выпуска одной фирмы влечет изменение выпуска другой фирмы. Это, как нетрудно заметить, опровергает первоначальное предположение об отсутствии реакции фирм на выпуски друг друга. Следовательно, в динамическом процессе производства гипотеза Курно оказывается несодержательной
Поиск по сайту: |
 число олигополистов и предположим, что все они выпускают один и тот же товар, применяя
число олигополистов и предположим, что все они выпускают один и тот же товар, применяя  видов затрат. Заметим, что при этом продукции разных фирм могут отличаться рядом признаков (качеством, оформлением и т.д.).
видов затрат. Заметим, что при этом продукции разных фирм могут отличаться рядом признаков (качеством, оформлением и т.д.). определяется объемом всех выпусков
определяется объемом всех выпусков  а цена затрат
а цена затрат  - объемом затрат всех фирм
- объемом затрат всех фирм  :
:


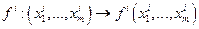 - производственная функция i-го олигополиста. Тогда производство описывается системой из
- производственная функция i-го олигополиста. Тогда производство описывается системой из 

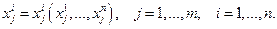


 - матрица затрат,
- матрица затрат, 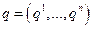 - вектор выпусков. Максимизация функции прибыли
- вектор выпусков. Максимизация функции прибыли  осуществляется только по переменным
осуществляется только по переменным  , выбором значений которых распоряжается i-ый олигополист.
, выбором значений которых распоряжается i-ый олигополист. зависит не только от экономического решения i-го олигополиста, но и от действий его конкурентов, распоряжающихся выбором
зависит не только от экономического решения i-го олигополиста, но и от действий его конкурентов, распоряжающихся выбором 

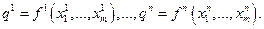
 Ситуация
Ситуация  называется равновесием по Нэшу в олигополии (7.2.2), если для любых i и
называется равновесием по Нэшу в олигополии (7.2.2), если для любых i и  имеет место неравенство
имеет место неравенство
 означает замену в ситуации
означает замену в ситуации 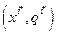 на пару
на пару  .
.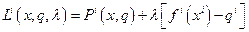
 и
и  ):
):
 , получаем
, получаем 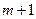 условие
условие (7.2.3)
(7.2.3) условий вида (7.2.3). Частные производные
условий вида (7.2.3). Частные производные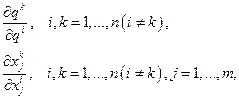 (7.2.4)
(7.2.4)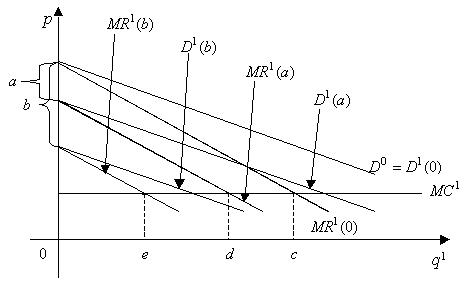
 где
где  Опираясь на правило оптимального поведения фирм о том, что максимизирующий прибыль фирмы объем выпуска должен соответствовать равенству предельного дохода и предельных издержек (см. (7.1.2) и (7.1.12)), которое верно и в случае олигополии, можно решить эту задачу графически (рис. 7.3).
Опираясь на правило оптимального поведения фирм о том, что максимизирующий прибыль фирмы объем выпуска должен соответствовать равенству предельного дохода и предельных издержек (см. (7.1.2) и (7.1.12)), которое верно и в случае олигополии, можно решить эту задачу графически (рис. 7.3). ) и линию рыночного спроса (на рис. 7.3 обозначена
) и линию рыночного спроса (на рис. 7.3 обозначена  ). Обозначим соответствующий выпуску
). Обозначим соответствующий выпуску  фирмы 2 предельный доход фирмы 1 через
фирмы 2 предельный доход фирмы 1 через  а соответствующий объему
а соответствующий объему 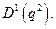
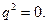 Тогда
Тогда  В этом случае оптимальный выпуск
В этом случае оптимальный выпуск 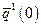 фирмы 1 найдем как пересечение линии предельного дохода
фирмы 1 найдем как пересечение линии предельного дохода  с линией предельных издержек
с линией предельных издержек 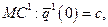 т.е., если фирма 2 ничего не производит, то фирма 1 должна выпустить
т.е., если фирма 2 ничего не производит, то фирма 1 должна выпустить  единиц продукции.
единиц продукции. . Тогда линия спроса
. Тогда линия спроса  смещается влево на
смещается влево на  единиц и
единиц и  Очевидно, что
Очевидно, что 
 получим
получим 
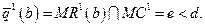


 оптимальных выпусков фирмы 1. Соединяя точки
оптимальных выпусков фирмы 1. Соединяя точки  ,
, 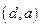 и
и  плавной линией, получим кривую реакции фирмы 1. Обозначим эту кривую через
плавной линией, получим кривую реакции фирмы 1. Обозначим эту кривую через  Точно так же можно построить кривую реакции фирмы 2
Точно так же можно построить кривую реакции фирмы 2  Изображение кривых реакций в пространстве
Изображение кривых реакций в пространстве  показано на рис. 7.4.
показано на рис. 7.4.
 кривых реакций отражает совпадение предположений обеих фирм об объеме выпуска конкурента и играет важную роль в принятии экономических решений дуополистами.
кривых реакций отражает совпадение предположений обеих фирм об объеме выпуска конкурента и играет важную роль в принятии экономических решений дуополистами. :
:

 - матрица затрат,
- матрица затрат,  - вектор выпусков,
- вектор выпусков,


 условий вида (7.2.3):
условий вида (7.2.3): (7.3.2)
(7.3.2)
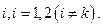
 (7.3.3)
(7.3.3)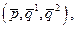 где
где  - соответствующая выпускам
- соответствующая выпускам  и
и  (в силу системы (7.3.1)) цена товара, называется равновесием Курно.
(в силу системы (7.3.1)) цена товара, называется равновесием Курно. (7.4.3)
(7.4.3) и
и  - цены и затраты, соответствующие (в силу системы (7.3.1)) равновесию Курно. Сумма в правой части равенства (7.3.4) есть предельный доход i -го дуополиста в состоянии равновесия Курно. Обозначим его через
- цены и затраты, соответствующие (в силу системы (7.3.1)) равновесию Курно. Сумма в правой части равенства (7.3.4) есть предельный доход i -го дуополиста в состоянии равновесия Курно. Обозначим его через  Если фирма 2 не реагирует на выпуск фирмы 1, то она не реагирует и на ее затраты. Поэтому при условии (7.3.3) предположения
Если фирма 2 не реагирует на выпуск фирмы 1, то она не реагирует и на ее затраты. Поэтому при условии (7.3.3) предположения (7.3.5)
(7.3.5)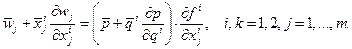 (7.3.6)
(7.3.6)

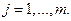 Поэтому, опуская индекс j и пользуясь формальным представлением (несколько игнорирующим математическую строгость обозначений, не влияющую на содержание)
Поэтому, опуская индекс j и пользуясь формальным представлением (несколько игнорирующим математическую строгость обозначений, не влияющую на содержание)  где
где  можем утверждать, что в состоянии равновесия Курно
можем утверждать, что в состоянии равновесия Курно  (7.3.7)
(7.3.7) где
где  а издержки фирм имеют вид
а издержки фирм имеют вид  где
где  - предельные издержки, а d - постоянные издержки.
- предельные издержки, а d - постоянные издержки. (7.3.8)
(7.3.8) (7.3.9)
(7.3.9) (7.3.10)
(7.3.10) поэтому
поэтому


 (7.3.11)
(7.3.11)



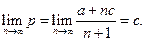
 ), когда олигополия превращается в рынок совершенной конкуренции, доля выпуска одной отдельно взятой фирмы становится ничтожно малой (по сравнению с суммарным выпуском всех фирм), а равновесная (уже в смысле Вальраса) цена равна предельным издержкам и не зависит от отдельных выпусков
), когда олигополия превращается в рынок совершенной конкуренции, доля выпуска одной отдельно взятой фирмы становится ничтожно малой (по сравнению с суммарным выпуском всех фирм), а равновесная (уже в смысле Вальраса) цена равна предельным издержкам и не зависит от отдельных выпусков  , а отрезок
, а отрезок  будем трактовать как один производственный цикл с началом в момент
будем трактовать как один производственный цикл с началом в момент  и концом в момент
и концом в момент  . В начале каждого производственного цикла дуополист принимает решение об объеме своего выпуска, исходя из информации о выпуске конкурента на предыдущем производственном цикле:
. В начале каждого производственного цикла дуополист принимает решение об объеме своего выпуска, исходя из информации о выпуске конкурента на предыдущем производственном цикле: (реакция фирмы 1),
(реакция фирмы 1),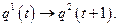 (реакция фирмы 2),
(реакция фирмы 2),
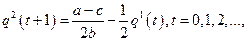
 (7.3.12)
(7.3.12) (7.3.13)
(7.3.13) с произвольного объема выпуска
с произвольного объема выпуска  фирмы 1, а вторая начинается в момент
фирмы 1, а вторая начинается в момент  фирмы 2. Совмещая значения последовательностей (7.3.12) и (7.3.13), как это показано на рис. 7.6, получаем последовательность выпусков
фирмы 2. Совмещая значения последовательностей (7.3.12) и (7.3.13), как это показано на рис. 7.6, получаем последовательность выпусков 












 подходит сколь угодно близко к равновесию Курно
подходит сколь угодно близко к равновесию Курно