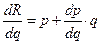|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Моделирование ценообразования в монополииСтр 1 из 3Следующая ⇒
Глава 7. Моделирование экономики в условиях несовершенной конкуренции
Моделирование ценообразования в монополии Определяющим признаком рынка в условиях совершенной конкуренции является наличие большого числа производителей и потребителей одних и тех же товаров и, как следствие, отсутствие влияния с их стороны на рыночные цены этих товаров (см. раздел 4.2). Нарушение данного условия приводит к понятию рынка несовершенной конкуренции. В этом смысле крайние положения занимают монополия и монопсония, а промежуточные - олигополия и олигопсония (см. рис. 1.3). Суть несовершенной конкуренции состоит в том, что либо продавцы, либо покупатели захватывают рыночную власть над ценообразованием. Начнем с анализа ценообразования в монополии. Так как монополист является единственным производителем товара, исходя из кривой спроса, он самостоятельно определяет объем продаж и цену товара (рис. 7.1).
Рис. 7.1 Выбор монополиста
Предположим, что в условиях совершенной конкуренции равновесие достигается в точке До какого уровня монополист будет повышать цену товара и снижать объем продаж, чтобы получить максимальную прибыль с учетом издержек на производство товара? Кривая спроса и оценка собственных издержек являются главными ориентирами для фирмы-монополиста при принятии экономического решения. Она принимает решение относительно объема выпуска (или продажи) товара, а его цена определяется с помощью кривой спроса (см. рис. 7.1). Следовательно, в условиях монополии цена Монополист может увеличить прибыль двумя путями: либо за счет повышения цены на товар, не изменяя при этом объема выпуска, либо за счет сокращения объема выпуска (снизив тем самым издержки на производство), не изменяя цену товара. Каково же оптимальное действие монополиста? Для ответа на этот вопрос обратимся к конкурентному рынку и рассмотрим долгосрочную задачу фирмы (3.5.1). Так как требуется узнать именно об оптимальном объеме производства, переформулируем эту задачу на языке выпуска. Обозначим доход как функцию от выпуска:
Так как издержки фирмы зависят от объема производства, они также являются функциями от выпуска:
Теперь задачу (3.5.1) можно записать так:
Условие первого порядка для максимизации прибыли
Следовательно, чтобы максимизировать прибыль, фирма должна достичь такого объема выпуска, при котором предельный доход равен предельным издержкам. Далее, учитывая тот факт, что
Рис. 7.2 Графическая иллюстрация равновесной цены
Графическая иллюстрация этого равенства показана на рис. 7.2, где предельные издержки есть возрастающая функция от объема производства, а предельный доход (цена) - убывающая функция того же аргумента. Вернемся к монополии и проверим, будет ли цена, максимизирующая прибыль монополиста, подчиняться закону (7.1.2)? В монополии
Далее без потери общности будем считать
Заметим, что и в монополии цена убывает с ростом объема продаж, потому что фирма снижает цену, чтобы продать больше продукции. Поэтому
Следовательно, в случае монополии предельный доход меньше цены товара. Проанализируем теперь издержки монополиста. Как и на конкурентном рынке, цены затрат являются функциями от объема затрат, т.е.
Будем предполагать, что
По рыночным законам фирма может покупать большее количество данного фактора производства, только предложив более высокую плату. Поэтому
Таким образом, в случае монополии предельные издержки на факторы производства оказываются больше их цен. Подставляя (7.1.3) и (7.1.5) в (7.1.1), получим оптимизационную задачу монополиста:
при ограничениях
Заметим, что в отличие от задачи (7.1.1) фирмы на конкурентном рынке, в условиях задачи монополиста (7.1.7) все цены зависят от объемов продуктов. Максимум функции прибыли P в задаче (7.1.7) вычисляется по
где
Отсюда имеем, в частности,
Сумма, стоящая в правой части равенства (7.1.8), есть предельный доход (см. (7.1.4)), а сумма, стоящая в правой части (7.1.9), - предельные издержки по производственному фактору j-го вида (см. (7.1.6)). Поэтому величина, стоящая в левой части (7.1.9), представляет собой произведение предельного дохода Исключая из системы необходимых условий множитель Лагранжа
Пользуясь равенствами (7.1.4) и (7.1.6), перепишем эту систему в виде
Оценим отношение предельной стоимости затрат на предельный продукт
Во-первых, как следует из (7.1.10), эта величина для всех j одна и та же. Во-вторых, издержки можно представить как функцию от выпуска, т.е.
Так как эта величина одна и та же для всех j, то, опуская индекс, из системы (7.1.10)-(7.1.11) получаем
Следовательно, чтобы максимизировать прибыль, монополист должен достичь такого уровня выпуска, при котором предельный доход равен предельным издержкам. Для монополиста мы получили такое же правило оптимального поведения, что и любая фирма в условиях конкурентного рынка. Однако в случае монополии выполняется равенство
и поэтому оптимальная цена товара отличается от выражения (7.1.2) в сторону повышения. А именно, через предельный доход она выражается как
а через предельные издержки –
Поиск по сайту: |

 , а доход данной фирмы, как участника рынка совершенной конкуренции, есть
, а доход данной фирмы, как участника рынка совершенной конкуренции, есть 
 . Будучи монополистом, при том же уровне спроса эта фирма добьется данного уровня дохода при меньшем выпуске
. Будучи монополистом, при том же уровне спроса эта фирма добьется данного уровня дохода при меньшем выпуске 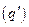 за счет более высокой цены
за счет более высокой цены  . Именно в этом заключается приоритетность положения монополиста.
. Именно в этом заключается приоритетность положения монополиста.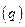 является функцией от выпуска
является функцией от выпуска 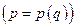 и, располагая информацией о спросе, фирма может добиться получения максимальной прибыли.
и, располагая информацией о спросе, фирма может добиться получения максимальной прибыли.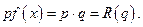

 . (7.1.1)
. (7.1.1) есть
есть или
или 
 получаем,
получаем, 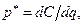 т.е. равновесная цена, если она существует, должна равняться предельным издержкам:
т.е. равновесная цена, если она существует, должна равняться предельным издержкам: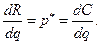 (7.1.2)
(7.1.2)
 поэтому
поэтому (7.1.3)
(7.1.3) Вычислим предельный доход
Вычислим предельный доход (7.1.4)
(7.1.4) и из (7.1.4) следует
и из (7.1.4) следует

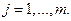 Поэтому издержки на факторы производства выражаются как
Поэтому издержки на факторы производства выражаются как (7.1.5)
(7.1.5) для всех
для всех 
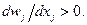 Тогда из (7.1.6) следует
Тогда из (7.1.6) следует

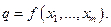 (7.1.7)
(7.1.7)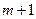 переменной
переменной 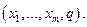 Поэтому составим функцию Лагранжа
Поэтому составим функцию Лагранжа
 - множитель Лагранжа. Выпишем необходимые условия оптимальности точки
- множитель Лагранжа. Выпишем необходимые условия оптимальности точки  :
:
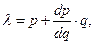 (7.1.8)
(7.1.8) (7.1.9)
(7.1.9) на предельный продукт j-го вида затрат
на предельный продукт j-го вида затрат  Это произведение можно трактовать как предельный доход j-го вида затрат.
Это произведение можно трактовать как предельный доход j-го вида затрат.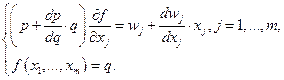
 (7.1.10)
(7.1.10)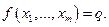 (7.1.11)
(7.1.11)
 Поэтому, пользуясь равенством (7.1.11), можно формально написать
Поэтому, пользуясь равенством (7.1.11), можно формально написать
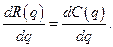 (7.1.12)
(7.1.12)