 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейный регрессионный анализ эконометрической модели
В регрессионном анализе изучается односторонняя зависимость переменной Пусть требуется найти аналитический вид (формулу вычисления) некоторого экономического показателя На первом шаге регрессионного анализа идентифицируют переменные
На втором шаге регрессионного анализа требуется спецификация формы связи между
Рис. 8.1. Примеры эмпирических зависимостей
Предположим, что в результате спецификации определена линейная зависимость между показателем
Задача третьего шага регрессионного анализа заключается в определении конкретных числовых значений параметров Естественно, линейные зависимости вида (8.2.1) наиболее просты для эконометрических исследований. Оказывается, что в ряде случаев к виду (8.2.1) можно привести и нелинейные зависимости с помощью логарифмирования, введения обратных величин и других приемов. Преобразование нелинейных функций в линейные называется линеаризацией. Покажем, в связи с этим, некоторые приемы линеаризации в случае двух переменных. Пусть нелинейное соотношение имеет гиперболический вид
Введем переменную Рассмотрим нелинейные зависимости степенного и показательного видов:
Прологарифмируем обе части каждого соотношения:
Обозначив
Таким образом, линеаризация расширяет область линейных моделей и повышает популярность линейных эконометрических методов. Однако опыт работы с экономическими данными показывает, что их отдельные значения не укладываются точно на прямую или на другую гладкую линию. Поэтому формализация вида (8.2.1) оказывается неадекватной целям, связанным с измерениями в экономике. Эта проблема преодолевается введением в соотношение (8.2.1) стохастического члена
Уравнение (8.2.2) называется линейной эконометрической моделью (или линейным уравнением регрессии
где неизвестными являются параметры Задача оценки неизвестных параметров уравнения (8.2.2) с помощью наблюдаемых значений переменных Пример 8.2. Исследуется соотношение между потребительскими расходами Совокупность статистических данных сгруппируем по численности и составу семей и рассмотрим связь между Эти рассуждения приводят к следующей гипотезе для нахождения искомого соотношения между потребительскими расходами и доходами: Замену функциональной зависимости (8.2.1) (т.е. математической модели показателя Y) статистической зависимостью (8.2.2) (т.е. эконометрической моделью показателя Y) можно обосновать следующими объективными причинами:
Дополнительное слагаемое Теоретической основой регрессионного анализа линейных эконометрических моделей типа (8.2.2) чаще других служит метод наименьших квадратов. Применение этого метода рассмотрим на примере парной регрессионной модели, т.е. линейной модели, состоящей из единственного уравнения, содержащего только две переменные:
Предположим, что проведено
(Так как рассматривается зависимость
Получим помощью наблюдаемых данных уравнение линии
которая будет наилучшей оценкой истинной линии
Необходимые условия оптимальности пары
Подставляя в эту систему значений выборочных наблюдений Систему (8.2.5) можно решить другим способом. Для этого проведем следующие преобразования. Разделив первое уравнение (8.2.5) на число
т.е. при найденных
Рис. 8.2. Оценочная линия
Вычитая (8.2.6) из (8.2.4) получим:
В этих обозначениях оценочное уравнение (8.2.4) запишется в виде:
а отклонение точки
Задача минимизации суммы квадратов отклонения:
относительно
Применяя достаточный признак оптимальности (см. (2.3.5)):
убеждаемся, что
Пример 8.3. Требуется выявить зависимость аварий на дорогах от количества автотранспорта для некоторого региона на основе результатов ежегодных наблюдений, заданных в следующей таблице:
Введем обозначения:
Система (8.2.5) принимает вид:
Решением ее будут параметры
Если же применять формулы (8.2.8) и (8.2.9), то необходимо предварительно вычислить
Поиск по сайту: |
 от одной или нескольких переменных
от одной или нескольких переменных  . Переменную
. Переменную 
 . Ориентиром для определения вида зависимости являются содержание решаемой задачи, результаты наблюдений за поведением показателя относительно изменения факторов на основе статистических данных. Например, выборочные наблюдения пар наблюдаемых значений
. Ориентиром для определения вида зависимости являются содержание решаемой задачи, результаты наблюдений за поведением показателя относительно изменения факторов на основе статистических данных. Например, выборочные наблюдения пар наблюдаемых значений  приведенные на Рис. 8.1a), говорят о линейном характере зависимости вида
приведенные на Рис. 8.1a), говорят о линейном характере зависимости вида  а на Рис 8.1b) - о полиномиальной зависимости вида
а на Рис 8.1b) - о полиномиальной зависимости вида 

 (8.2.1)
(8.2.1) на основе статистических данных о наблюдениях значений
на основе статистических данных о наблюдениях значений 

 . Тогда это соотношение становится линейным относительно
. Тогда это соотношение становится линейным относительно 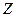 :
: 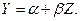




 получаем линейные соотношения
получаем линейные соотношения (относительно
(относительно  ),
), (относительно
(относительно  ).
). :
: . (8.2.2)
. (8.2.2)
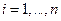 , из
, из  наблюдений над переменными
наблюдений над переменными 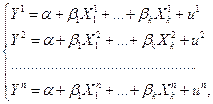
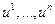 .
. называется линейным регрессионным анализом.
называется линейным регрессионным анализом. и доходами
и доходами  с использованием данных
с использованием данных  о семейных бюджетах
о семейных бюджетах 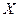 в каждой конкретной группе. Внутри группы выберем семьи, имеющие один и тот же доход
в каждой конкретной группе. Внутри группы выберем семьи, имеющие один и тот же доход  . Очевидно, расходы этих семей будут разными. Однако можно указать такой уровень расходов
. Очевидно, расходы этих семей будут разными. Однако можно указать такой уровень расходов  , вокруг которого будут сгруппированы расходы всех семей этой подгруппы. Предположим, что для
, вокруг которого будут сгруппированы расходы всех семей этой подгруппы. Предположим, что для  где
где  . Обозначим через
. Обозначим через 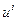 величину отклонения расходов
величину отклонения расходов  -й семьи от «центрального» значения
-й семьи от «центрального» значения 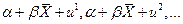 Причем
Причем  Слагаемое
Слагаемое  и ошибку
и ошибку 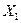


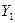
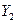

 , показывают наблюдаемые значения
, показывают наблюдаемые значения 

 , (8.2.4)
, (8.2.4)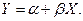 Согласно методу наименьших квадратов эти параметры
Согласно методу наименьших квадратов эти параметры  и
и  являются решением оптимизационной задачи
являются решением оптимизационной задачи
 имеют вид (см. (2.3.3)):
имеют вид (см. (2.3.3)): (8.2.5)
(8.2.5) , получим линейную систему из двух уравнений с двумя неизвестными
, получим линейную систему из двух уравнений с двумя неизвестными  (8.2.6)
(8.2.6)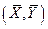 (Рис. 8.2 ).
(Рис. 8.2 ).
 Отклонения наблюдаемых значений
Отклонения наблюдаемых значений  ,
, 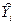 от их средних обозначим малыми буквами:
от их средних обозначим малыми буквами:
 , (8.2.7)
, (8.2.7) от этой линии в виде
от этой линии в виде

 . (8.2.8)
. (8.2.8) ,
, . Параметр
. Параметр  (8.2.9)
(8.2.9) ;
;  - количество транспорта в год
- количество транспорта в год  С помощью данных столбиков (3) и (4) вычислим коэффициенты для системы (8.2.5):
С помощью данных столбиков (3) и (4) вычислим коэффициенты для системы (8.2.5):


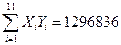

 Следовательно, оценочное уравнение запишется в виде
Следовательно, оценочное уравнение запишется в виде 


 и
и 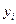 (см. таблицу). Далее, подставляя эти значения в упомянутые формулы, находим
(см. таблицу). Далее, подставляя эти значения в упомянутые формулы, находим ,
, .
.