 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эконометрика как приложение математической статистики в экономикеСтр 1 из 4Следующая ⇒
Глав 8. Эконометрическое моделирование
Под статистическими данными понимают систематизированные и группированные однородные, количественные сведения о реальной экономической деятельности за прошлые периоды времени или результаты многократно проводимых экспериментов и наблюдений. Такие данные играют важную роль в экономико-математическом моделировании, в частности, для
На стыке экономической практики и математической статистики в начале 30-х годов зародилась новая самостоятельная дисциплина, получившая название «Эконометрика». Эконометрика - это наука, которая изучает статистические закономерности в экономике. Методологическая особенность эконометрики заключается в применении достаточно общих гипотез о статистических свойствах экономических параметров и ошибок при их измерении. Полученные при этом результаты могут оказаться нетождественными тому содержанию, которое вкладывается в реальный объект. Поэтому важная задача эконометрики - создание как более универсальных, так и специальных методов для обнаружения наиболее устойчивых характеристик в поведении реальных экономических показателей. Эконометрика разрабатывает методы подгонки формальной модели с целью наилучшего имитирования ею поведения моделируемого объекта на основе гипотезы о том, что отклонения модельных значений параметров от их реально наблюдаемых случайны и вероятностные характеристики их известны. Математическая статистика является тем универсальным аппаратом, который удачно вписывается в содержание различных эконометрических исследований. Такие ее разделы, как корреляционный и регрессионный анализы, метод наименьших квадратов и прогнозирование, наилучшим образом подходят для выявления статистических закономерностей в экономике. Корреляционный анализ позволяет количественно оценить связи между большим числом взаимодействующих экономических явлений как между случайными величинами. Его применение делает возможным проверку различных экономических гипотез о наличии и силе связи между двумя величинами или группой величин. Корреляционный анализ тесно связан с регрессионным анализом, задача которого состоит в экспериментальном определении параметров корреляционных зависимостей между экономическими показателями путем наблюдения за характером их изменения. Одним из основных методов регрессионного анализа является метод наименьших квадратов. Модели, полученные с помощью регрессионного анализа, позволяют прогнозировать варианты развития экономических процессов и явлений, изучить тенденции изменения экономических показателей, т.е. служат инструментом научно-обоснованных предсказаний. Результаты прогноза являются исходным материалом для постановки реальных экономических целей и задач, для выявления и принятия наилучших управленческих решений, для разработки хозяйственной и финансовой стратегий в будущем. Являясь составной частью математической экономики, эконометрика вполне естественно вписывается в общий алгоритм экономико-математических исследований. Эконометрические исследования начинаются после того, как
Пример 8.1. Предположим, что для моделирования экономической динамики на некотором временном интервале требуется описать математически зависимость таких макропоказателей, как потребление, инвестиции и национальный доход от некоторых наиболее существенных факторов. Пусть на гуманитарном этапе исследования экономисты выяснили, что
Для нахождения аналитического вида этих трех показателей введем обозначения:
Переменные
где При помощи несложных преобразований можно все зависимые переменные выразить через независимые переменные:
Теперь можно проводить некоторый качественный анализ параметров модели. Во-первых, как следует из первого и третьего равенств, для положительной знакоопределенности потребления и национального дохода должно быть Следовательно, выводы, получаемые из модели, не противоречат действительности и говорят в пользу правильного выбора модели. Однако эта качественная информация является чисто априорной и нуждается в подтверждении численными данными. В частности, с помощью численной информации требуется подтвердить гипотезу о линейности модели и в противном случае рассмотреть более сложные зависимости; сравнить численно эффективность влияния отдельных экзогенных переменных на каждую эндогенную переменную; проверить устойчивость модели на изменение численных значений параметров и т.д. Наконец, отметим еще одну важную проблему, которую нельзя решить без дополнительных статистических преобразований. Речь идет об уравнениях, имеющих в (8.1.1) форму точных функциональных зависимостей. Дело в том, что ни для каких реальных экономических данных нельзя обеспечить постоянного соблюдения простых соотношений, имеющих линейную или иную несложную форму. В модели (8.1.1) учтены, возможно, самые существенные факторы (экзогенные переменные), от которых зависят эндогенные показатели, но явно не все - за рамками модели осталось множество так называемых второстепенных факторов. Поэтому для обеспечения равенства между левыми и правыми частями, в каждое соотношение приходится вводить возмущающую величину (стохастическую ошибку):
где Таким образом, существует достаточно много аргументов, в силу которых качественной информации о параметрах модели недостаточно и ее необходимо заменить количественной информацией, добываемой с помощью статистических данных. Эконометрика как раз и занимается методами получения лучших оценок параметров эконометрических моделей, конструируемых в прикладных целях. Эконометрические модели по сравнению с аналитическими более точны и подробны, не требуют грубых допущений и упрощений, позволяют учесть большое число факторов. Основные их недостатки - громоздкость, плохая обозримость, большой расход машинного времени при их построении и анализе и крайняя трудность поиска оптимальных решений, которые приходится искать путем догадок и проб (в отличие от более приспособленных к оптимизационным задачам аналитических моделей). Наиболее эффективная методика экономико-математических исследований - это совместное применение аналитических и эконометрических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить контуры основных закономерностей. Уточнение же этих закономерностей - прерогатива эконометрических моделей. С этой точки зрения важная задача эконометрики - проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале при помощи методов математической статистики. В общем случае эконометрическая модель может содержать несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью достаточно сложных методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов ограничимся в дальнейшем рассмотрением простой линейной регрессии. Термин регрессия используется для описания природы связи между переменными, а термин корреляция - для измерения тесноты связи. По мере возрастания сложности после статистического анализа, который касается поведения отдельных переменных, идет линейная регрессия с двумя переменными (парная регрессия). Простая линейная регрессия связана с тем, что называется двумерным распределением случайных величин, т.е. распределением двух переменных. Очевидно, использование двух переменных дает большую информацию, чем использование одной. Например, доход от продажи товара можно анализировать, используя только данные о доходе на прошлых периодах времени вне связи с другими факторами (статистический анализ). Более богатую информацию можно получить, если принять во внимание другие факторы, которые влияют на объем продаж: спрос, цена товара, цена товара-конкурента, период времени, затраты на рекламу и др. Если при этом расходы на рекламу явились бы главным фактором, определяющим объем продаж, то знание вида связи объема продаж и расходов на рекламу было бы весьма полезным для планирования финансовой политики компании. Точно так же могут интересовать двумерные распределения объема продаж и цены товара, дохода от продаж и уровня спроса и т.д. Другими примерами линейной регрессии с двумя переменными могли бы быть соотношения между издержками производства и квалификацией рабочих, между качеством продукции и продолжительностью рабочего дня, между весом и возрастом кур и т.д. Линейную регрессию, как математическую модель, можно использовать для того, чтобы делать какие-то прогнозы или предсказания. Например, любая курица, реальный вес которой значительно отличается от прогнозируемого среднего веса, может быть подвергнута обследованию. В результате последующего анализа могут быть выявлены причины отклонения веса и приняты меры по улучшению рациона питания или изменению режима обслуживания и условий содержания. Основным недостатком, присущим линейным эконометрическим моделям с двумя переменными, является их неадекватность к реальной действительности. Это вызвано, во-первых, тем, что статистическая (и, в частности, корреляционная) зависимость между экономическими величинами практически никогда не бывает в чистом виде линейной; во-вторых, многие факторы, влияющие на эти две переменные, остаются за пределами модели, т.е. оказываются неучтенными. Однако эти недостатки довольно успешно устраняются с помощью специальных эконометрических приемов.
Поиск по сайту: |
 - параметр времени (год t);
- параметр времени (год t);  - потребление в год t;
- потребление в год t;  - инвестиции в год t;
- инвестиции в год t;  - национальный доход в год t;
- национальный доход в год t;  - государственные закупки в год t;
- государственные закупки в год t;  - подоходный налог в год t;
- подоходный налог в год t;  - фактор государственного регулирования в год t.
- фактор государственного регулирования в год t. являются эндогенными (внутренними, неизвестными), а
являются эндогенными (внутренними, неизвестными), а 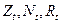 - экзогенными (внешними, заданными). При описании взаимосвязи между экзогенными и эндогенными переменными, прежде всего, нужно сделать гипотезу о характере пропорциональности этих зависимостей, о типе функций (линейные, нелинейные), о виде функций (полиномиальные, степенные, логарифмические и т.д.). Для окончательного решения этого вопроса требуются многократные эксперименты. При первоначальном анализе обычно выбирают наиболее простые зависимости. Поэтому на основе указанных выше положений можно начать со следующих линейных зависимостей:
- экзогенными (внешними, заданными). При описании взаимосвязи между экзогенными и эндогенными переменными, прежде всего, нужно сделать гипотезу о характере пропорциональности этих зависимостей, о типе функций (линейные, нелинейные), о виде функций (полиномиальные, степенные, логарифмические и т.д.). Для окончательного решения этого вопроса требуются многократные эксперименты. При первоначальном анализе обычно выбирают наиболее простые зависимости. Поэтому на основе указанных выше положений можно начать со следующих линейных зависимостей:
 , а
, а  - параметры задачи, показывающие реакцию эндогенных переменных в текущем времени на изменение экзогенных и лаговых эндогенных переменных
- параметры задачи, показывающие реакцию эндогенных переменных в текущем времени на изменение экзогенных и лаговых эндогенных переменных 
 (8.1.1)
(8.1.1) ; как следует из второго равенства и содержательного смысла инвестиций, должно быть
; как следует из второго равенства и содержательного смысла инвестиций, должно быть 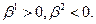 Во-вторых, поскольку модель (8.1.1) линейная, эффект от одновременного изменения нескольких экзогенных переменных будет равен сумме частных эффектов. Так, одновременное увеличение на единицу объема государственных закупок и налога оставит потребление и инвестиции неизменными, а соответствующий прирост национального дохода будет равен единице. В-третьих, можно анализировать реакцию показателей на изменение каждого фактора. Например, увеличение на одну единицу значения фактора государственного регулирования вызовет изменение потребления на величину
Во-вторых, поскольку модель (8.1.1) линейная, эффект от одновременного изменения нескольких экзогенных переменных будет равен сумме частных эффектов. Так, одновременное увеличение на единицу объема государственных закупок и налога оставит потребление и инвестиции неизменными, а соответствующий прирост национального дохода будет равен единице. В-третьих, можно анализировать реакцию показателей на изменение каждого фактора. Например, увеличение на одну единицу значения фактора государственного регулирования вызовет изменение потребления на величину  , а инвестиций – на
, а инвестиций – на 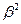 , т.е. усиление государственного регулирования уменьшит и потребление, и инвестиции. Такой содержательный анализ можно продолжить и дальше.
, т.е. усиление государственного регулирования уменьшит и потребление, и инвестиции. Такой содержательный анализ можно продолжить и дальше.
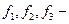 обозначения правых частей уравнения (8.1.1). Стохастические ошибки
обозначения правых частей уравнения (8.1.1). Стохастические ошибки  можно оценить только с помощью статистических данных и теоретико-вероятностных методов. Такие модели принято называть эконометрическими моделями.
можно оценить только с помощью статистических данных и теоретико-вероятностных методов. Такие модели принято называть эконометрическими моделями.