 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Конструирование и оценка производственных функций
Все рассмотренные применения производственных функций имеют место на практике экономических исследований и приносят реальную пользу только в том случае, если они как модели взаимосвязи затраты-выпуск будут адекватно отражать действительность. Поэтому важной задачей теории является разработка достоверных и реалистических методов построения производственных функций. По существу, производственная функция
Рис. 3.2 Схема превращения ресурсов в конечный продукт
В блоке Из сказанного следует, что для построения производственных функций нужно знать технологию производства, ее структуру и организацию, а также принципы работы сложных машин и оборудования, т.е. надо быть одновременно и технологом, и инженером, и математиком. Оказывается, что знание всего этого сложного производственного механизма не требуется, если владеть подходящими математическими приемами. Речь идет об использовании методов регрессионного анализа на основе статистических (опытных, экспертных) данных о затратах и выпуске. Не умаляя достоинства других математических и иных методов построения производственных функций, можно сказать, что именно методы регрессионного анализа наилучшим образом оправдали себя на практике и потому являются наиболее популярными. Рассмотрим только содержательной стороны построения конкретных видов производственных функций. Идею применения статистических данных для построения производственной функции можно объяснить на рисунке 4.2. Имеются известные величины
Например, свою знаменитую функцию (3.2.4) Кобб и Дуглас получили на основе изучения статистических данных по расходованию капитала (K), труда (L) и индекса производства (Y) в американской обрабатывающей промышленности за период с 1899 по 1922 гг. Практическая значимость этой функции подтверждается тем, что соответствующая замена исходных данных позволяет использовать ее для анализа любого производства. Рассмотрим этапы построения производственной функции. Пусть известны виды ресурсов 1. спецификация функции f, т.е. выявление общего вида функции f от аргументов 2. оценка параметров - определение конкретных числовых значений неизвестных параметров. Картина расположения статистических данных в пространстве затраты-выпуск может подсказать линейный или нелинейный характер зависимости функции f от аргументов
в случае производственной функции Кобба-Дугласа - в виде мультипликативной функции
в случае производственной функции CES - в виде степенного многочлена
и т.д. Здесь Чаще остальных на практике применяется аппроксимация вида (3.4.1), называемая линейной регрессией. Для определения ее параметров используется (линейный) метод наименьших квадратов. В некоторых случаях к линейной аппроксимации удается свести и нелинейные относительно ресурсов производственные функции. Например, логарифмируя функцию (3.4.2), получим:
Вводя обозначения
приходим к линейной регрессии вида (3.4.1):
Применяя такой способ на основе статистических данных рассмотренного периода, Кобб и Дуглас получили следующую оценку параметров для своей функции:
и, следовательно, их производственная функция выглядела так:
Дальнейший анализ показал, что за исключением некоторых случаев (например, учета технического прогресса), имеет место соотношение В отличие от функции Кобба-Дугласа, функция (3.4.3) даже после логарифмирования остается нелинейной. Поэтому для оценки параметров функции CES применяется более сложный нелинейный метод наименьших квадратов. При спецификации производственной функции, т.е. при решении вопроса о принадлежности этой функции к тому или иному классу известных функций, может быть полезным знание тех или иных числовых характеристик этих классов функций (отношение средних и предельных показателей, предельная норма замещения, эластичность и др.). Например, при моделировании двухфакторного производства
Если эта величина приблизительно равна постоянному числу для всех t и
Поиск по сайту: |
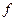 есть совокупность правил, с помощью которых для каждого набора затрат
есть совокупность правил, с помощью которых для каждого набора затрат  определяется соответствующий выпуск
определяется соответствующий выпуск  :
:  . Поэтому построение производственной функции означает нахождение математической формулы, отражающей эти правила или, иначе говоря, закономерности превращения набора ресурсов в конечный продукт. Этот процесс условно можно представить схемой:
. Поэтому построение производственной функции означает нахождение математической формулы, отражающей эти правила или, иначе говоря, закономерности превращения набора ресурсов в конечный продукт. Этот процесс условно можно представить схемой:
 в определенных пропорциях таким образом, чтобы получился требуемый продукт. Эти пропорции определяются спецификой производства и математически выражаются с помощью различных коэффициентов и показателей степени для величин
в определенных пропорциях таким образом, чтобы получился требуемый продукт. Эти пропорции определяются спецификой производства и математически выражаются с помощью различных коэффициентов и показателей степени для величин  (реальные результаты производства) и одно неизвестное выражение
(реальные результаты производства) и одно неизвестное выражение  .
.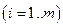 , используемых для выпуска данной продукции, и имеется необходимое количество статистических данных по объемам затрат
, используемых для выпуска данной продукции, и имеется необходимое количество статистических данных по объемам затрат  и свободным членом);
и свободным членом); , (3.4.1)
, (3.4.1) , (3.4.2)
, (3.4.2) (3.4.3)
(3.4.3)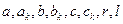 являются неизвестными параметрами, подлежащими определению (оценке).
являются неизвестными параметрами, подлежащими определению (оценке). .
.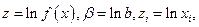
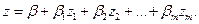




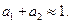 Так как величина
Так как величина  показывает эластичность производства, равенство
показывает эластичность производства, равенство  является признаком линейной однородности производственной функции. Этот факт позволяет записывать функцию Кобба-Дугласа в виде
является признаком линейной однородности производственной функции. Этот факт позволяет записывать функцию Кобба-Дугласа в виде  где
где 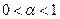 .
. на основе имеющейся статистики
на основе имеющейся статистики  можно составить дискретный (разностный) аналог показателя эластичности по капиталу
можно составить дискретный (разностный) аналог показателя эластичности по капиталу
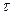 , для которых разность
, для которых разность  достаточно мала, то искомая функция может принадлежать классу функций Кобба-Дугласа. Точно так же, дискретный аналог эластичности замещения может внести ясность относительно принадлежности искомой функции к классу функций CES.
достаточно мала, то искомая функция может принадлежать классу функций Кобба-Дугласа. Точно так же, дискретный аналог эластичности замещения может внести ясность относительно принадлежности искомой функции к классу функций CES.