 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пространство затрат и производственная функция
Предположим, что фирма производит Использование двойной индексации привлекательно с точки зрения информативности (видно, какой ресурс относится к какому продукту), но неудобно чисто технически. Во-первых, усложняется запись формул; во-вторых, увеличивается размерность задачи (т.к. среди Поэтому в дальнейшем виды ресурсов будем обозначать одинарными индексами Введем в рассмотрение два вида векторов:
называется пространством затрат. Аналогично определяется пространство выпуска:
Для отражения реальных возможностей фирмы в математических моделях часто применяются подмножества Технологическая связь между затратами и выпуском описывается с помощью производственной функции. Определение 3.1. Функция Это определение является определением производственной функции для многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма выпускает только один вид продукта, то производственная функция является скалярной:
В общем случае производственную функцию можно записать в неявной форме: Если в качестве независимых переменных (аргументов) выступают затраты (см. (3.2.1)), то производственную функцию иногда называют функцией выпуска, если же фиксирована величина выпуска Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др. Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основными из них являются следующие: · в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы; · все величины должны иметь отчетливый экономический смысл; · все экономические величины, входящие в производственную функцию, должны быть измеримы; · выпуск продукции без затрат невозможен; · если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно; · увеличение затрат не может привести к уменьшению выпуска. Вопрос об адекватном описании экономической реальности на языке производственных функций тесно связан с их математическими свойствами. Для простоты изложения эти свойства приведем для однопродуктового производства, т.е. для производственной функции вида (3.2.1) . 1. Монотонность: из 2. Вогнутость: для любых
3. Поведение в начале координат: 4. Однородность: Если производственная функция дифференцируема по всем аргументам, то свойства 1 и 2 соответственно могут быть заменены следующими неравенствами:
Частные производные Свойство 3 является отражением бездеятельности, так как без затрат нет и выпуска. Свойство 4 описывает реакцию производства на изменение затрат. Параметр
то говорят о возрастающем (убывающем) доходе от расширения масштаба производства. Заметим, что свойство 4 определено в точке, тогда как свойства 1 и 2 - во всем пространстве затрат. Таким образом, перечисленные (желательные) свойства производственной функции вполне согласуются с ее определением, так как они касаются только соотношения затраты-выпуск. Действительно, здесь нет никаких требований на бесперебойную работу станков, нормирования движения конвейера и т.д. Поэтому производственная функция, как отображение количественной связи между затратами и выпуском, представляет собой регрессионную модель (см. раздел 2.5). Следовательно, она может быть построена на основе статистических данных и с применением методов математической статистики. Приведем примеры наиболее удачно построенных и потому часто применяемых на практике производственных функций. При этом для простоты будем рассматривать двухфакторную однопродуктовую производственную функцию вида
1. Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:
где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда,
Легко проверить, что
Кроме того, функция (3.2.4) линейно-однородна:
Таким образом, функция Кобба-Дугласа (3.2.4) обладает всеми вышеуказанными свойствами. Для многофакторного производства функция Кобба-Дугласа имеет вид:
Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса)
где не обязательно 2. Производственная функция CES(с постоянной эластичностью замещения) имеет вид:
где
то функция (3.2.5) удовлетворяет неравенствам (3.2.2) и (3.2.3). С учетом технического прогресса функция CES записывается в виде
Название данной функции следует из того факта, что для нее эластичность замещения постоянна (см. раздел 3.3). 3. Производственная функция с фиксированными пропорциями. Эта функция получается из (3.2.5) при
4. Производственная функция затрат-выпуска(функция Леонтьева) получается из (3.2.6) при
Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:
или
где 5. Производственная функция анализа способов производственной деятельности. Данная функция обобщает производственную функцию затрат-выпуска на случай, когда существует некоторое число
где 6. Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:
где Среди приведенных производственных функций наиболее общей является функция CES. Действительно, используя понятия предельной нормы замещения и эластичности замещения, она обобщает функции Кобба-Дугласа, Леонтьева и линейную производственную функцию. Можно показать, что функции (3.2.5) - (3.2.9) соответствуют свойствам 3, 4 и условиям (3.2.2), (3.2.3). Для анализа процесса производства и различных его показателей наряду с предельными продуктами,
(верхние черточки обозначают фиксированные значения переменных), показывающими величины дополнительных доходов, получаемых при использовании дополнительных количеств затрат, применяются понятия средних продуктов. Средним продуктом по
Зафиксируем затраты второго вида на некотором уровне
Рис. 3.1 Кривые выпуска
Пусть график функции Для конкретных наименований ресурсов средние и предельные величины приобретают смысл конкретных экономических показателей. Рассмотрим, например, функцию Кобба-Дугласа (3.2.4), где
имеют смысл соответственно средней производительности труда и средней производительности капитала (средней фондоотдачи). Очевидно, средняя производительность труда убывает с ростом трудовых ресурсов. Действительно, производственные фонды (K) остаются неизменными, и потому вновь привлекаемая рабочая сила не обеспечивается дополнительными средствами производства, что и приводит к снижению производительности труда. Аналогичное рассуждение верно и для фондоотдачи как функции от капитала. Для функции (3.2.4) предельные продукты
имеют смысл соответственно предельной производительности труда и предельной производительности капитала (предельной фондоотдачи). В микроэкономической теории производства считается, что предельная производительность труда
Поиск по сайту: |
 видов продуктов. Виды продуктов будем обозначать индексом
видов продуктов. Виды продуктов будем обозначать индексом  , а их количества - через
, а их количества - через  Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами
Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами  обозначим виды ресурсов, используемых для выпуска продукта вида
обозначим виды ресурсов, используемых для выпуска продукта вида  Пусть
Пусть 
 Обозначим через
Обозначим через  - количества этих ресурсов. Следовательно, имеется всего
- количества этих ресурсов. Следовательно, имеется всего  видов ресурсов.
видов ресурсов. могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.). , их количества -
, их количества - 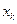 , где
, где  Здесь
Здесь 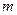 - достаточно большое число (равное сумме
- достаточно большое число (равное сумме  .
. - вектор затрат и
- вектор затрат и  - вектор выпуска. Положительный ортант
- вектор выпуска. Положительный ортант
 .
. и
и 
 ставящая в соответствие каждому вектору затрат
ставящая в соответствие каждому вектору затрат  вектор
вектор  максимального выпуска, который может быть получен при этих затратах, называется производственной функцией.
максимального выпуска, который может быть получен при этих затратах, называется производственной функцией. или
или . (3.2.1)
. (3.2.1)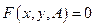 , где A -
, где A -  -матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции:
-матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции:  , где переменные
, где переменные  со знаком «
со знаком «  » обозначают затраты, а со знаком «+» - выпуски.
» обозначают затраты, а со знаком «+» - выпуски. , то производственная функция является функцией затрат
, то производственная функция является функцией затрат  Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями.
Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями. и
и  следует
следует 
 справедливо неравенство
справедливо неравенство

 где
где  - масштабное число,
- масштабное число,  - степень однородности.
- степень однородности. , (3.2.2)
, (3.2.2) (3.2.3)
(3.2.3) называются предельными продуктами. Условие (3.2.2) , как и свойство 1, означает, что увеличение любого вида затрат не приводит к уменьшению выпуска. Условие (3.2.3) показывает, что увеличение затрат одного вида ресурса (при постоянном уровне затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство в экономической теории называется законом убывающей доходности (отдачи).
называются предельными продуктами. Условие (3.2.2) , как и свойство 1, означает, что увеличение любого вида затрат не приводит к уменьшению выпуска. Условие (3.2.3) показывает, что увеличение затрат одного вида ресурса (при постоянном уровне затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство в экономической теории называется законом убывающей доходности (отдачи). показывает масштаб изменения производства (расширения производства - если
показывает масштаб изменения производства (расширения производства - если  , сужения производства – если
, сужения производства – если  ), а
), а  - эффект от изменения масштабов производства. Если
- эффект от изменения масштабов производства. Если 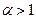 , то одновременное увеличение всех факторов в
, то одновременное увеличение всех факторов в  , т.е. эффект от расширения масштаба производства положителен. При
, т.е. эффект от расширения масштаба производства положителен. При  получаем:
получаем:  - выпуск возрастает в той же пропорции, что и затраты. Такие функции называются линейно-однородными (или однородными в первой степени). Если
- выпуск возрастает в той же пропорции, что и затраты. Такие функции называются линейно-однородными (или однородными в первой степени). Если

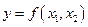

 (3.2.4)
(3.2.4) - числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде
- числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде

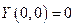 и
и



 , где
, где  - параметр времени,
- параметр времени,  - постоянное число, характеризующее темп развития. В результате функция принимает «динамический» вид:
- постоянное число, характеризующее темп развития. В результате функция принимает «динамический» вид:
 , причём показатели степени в функции (3.2.4) имеют смысл эластичности выпуска по капиталу и труду.
, причём показатели степени в функции (3.2.4) имеют смысл эластичности выпуска по капиталу и труду. , (3.2.5)
, (3.2.5) - коэффициент шкалы,
- коэффициент шкалы,  - коэффициент распределения,
- коэффициент распределения,  - коэффициент замещения,
- коэффициент замещения,  - степень однородности. Если выполнены условия
- степень однородности. Если выполнены условия
 .
. и имеет вид:
и имеет вид: (3.2.6)
(3.2.6) :
: .
. (3.2.7)
(3.2.7)
 - количество затрат вида
- количество затрат вида  - выпуск.
- выпуск. базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид «оптимизационной задачи»
базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид «оптимизационной задачи» где
где  (3.2.8)
(3.2.8) - выпуск продукции при единичной интенсивности
- выпуск продукции при единичной интенсивности  - уровень интенсивности,
- уровень интенсивности,  - количество затрат вида
- количество затрат вида 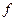 по
по  в (3.2.8) при заданных ограничениях-неравенствах является моделью анализа производственной деятельности (максимизация выпуска при ограниченных ресурсах).
в (3.2.8) при заданных ограничениях-неравенствах является моделью анализа производственной деятельности (максимизация выпуска при ограниченных ресурсах). (3.2.9)
(3.2.9) - норма затрат k-го вида для производства единицы продукции (предельный физический продукт затрат).
- норма затрат k-го вида для производства единицы продукции (предельный физический продукт затрат).


 .
. и сравним графики трех функций:
и сравним графики трех функций:

 имеет три критические точки (см. Рис.3.1):
имеет три критические точки (см. Рис.3.1):  - точка перегиба,
- точка перегиба, 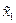 - точка касания с лучом из начала координат,
- точка касания с лучом из начала координат,  - точка максимума. Эти точки соответствуют трем стадиям производства. Первая стадия соответствует отрезку
- точка максимума. Эти точки соответствуют трем стадиям производства. Первая стадия соответствует отрезку  и характеризуется превосходством предельного продукта над средним:
и характеризуется превосходством предельного продукта над средним:  Следовательно, на этой стадии осуществление дополнительных затрат целесообразно. Вторая стадия соответствует отрезку
Следовательно, на этой стадии осуществление дополнительных затрат целесообразно. Вторая стадия соответствует отрезку  и характеризуется превосходством среднего продукта над предельным:
и характеризуется превосходством среднего продукта над предельным:  (дополнительные затраты не целесообразны). На третьей стадии
(дополнительные затраты не целесообразны). На третьей стадии 
 и дополнительные затраты приводят к обратному эффекту. Это объясняется тем, что
и дополнительные затраты приводят к обратному эффекту. Это объясняется тем, что  - капитал, а
- капитал, а  - труд. Средние продукты
- труд. Средние продукты



 равна заработной плате (цене труда), а предельная производительность капитала
равна заработной плате (цене труда), а предельная производительность капитала  - рентным платежам (цене услуг капитальных благ). Из условия (3.2.2) следует, что при неизменных основных фондах (трудовых затратах) увеличение численности работающих (объема основных фондов) приводит к падению предельной производительности труда (предельной фондоотдачи). Видно, что для функции Кобба-Дугласа предельные продукты пропорциональны средним продуктам и меньше их.
- рентным платежам (цене услуг капитальных благ). Из условия (3.2.2) следует, что при неизменных основных фондах (трудовых затратах) увеличение численности работающих (объема основных фондов) приводит к падению предельной производительности труда (предельной фондоотдачи). Видно, что для функции Кобба-Дугласа предельные продукты пропорциональны средним продуктам и меньше их.