 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Способы задания функции
Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции. Существует три основных способа задания функции: аналитический, табличный и графический. Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента. Например, Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию. Табличный способ предусматривает задание таблицы, в которой различным значениям аргумента
Такие таблицы составляются, например, по данным эксперимента; для облегчения вычислений с часто встречающимися функциями (таблицы логарифмов, таблицы тригонометрических функций и т.д.). Графический способ задания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.
Основные элементарные функции Основными элементарным функциями называются следующие функции: 1) Степенная функция
2) Показательная функция
3) Логарифмическая функция
4) Тригонометрические функции
5) Обратные тригонометрические функции
Сложная функция Из основных элементарных функций можно строить другие функции при помощи новой операции взятия функции от функции. Пусть y является функцией от u, т.е.
Функция Переменную Операция взятия функции от функции может проводиться любое число раз. Например, функция Сложная функция может иметь несколько промежуточных аргументов.
Обратная функция Определение. Пусть функция
Рис. 1.3
Поскольку традиционно независимую переменную принято обозначать через х, а зависимую (функцию) – через y, то обратная функция для х примет вид:
Элементарные функции Определение. Функции, полученные из основных элементарных функций и постоянных при помощи конечного числа арифметических действий и конечного числа операций взятия функции от функции, называются элементарными функциями. Например, Элементарные функции делятся на алгебраические и трансцендентные. К алгебраическим относятся следующие функции: 1) Целая рациональная функция или многочлен:
где Например, 2) Дробная рациональная функция. Эта функция является отношением двух многочленов:
Например, 3) Иррациональная функция. Например, Функция, не являющаяся алгебраической, называется трансцендентной. Например,
Поиск по сайту: |
 ;
;  ;
; 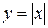 , где
, где  .
. поставлены соответствующие значения функции
поставлены соответствующие значения функции  :
: ,
,  .
. .
. .
. .
. .
. , а u, в свою очередь, зависит от переменной х, т.е.
, а u, в свою очередь, зависит от переменной х, т.е.  . Тогда y также зависит от х:
. Тогда y также зависит от х: .
. есть суперпозиция трех функций
есть суперпозиция трех функций  ,
,  и
и  .
.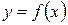 , определена на множестве Х с областью значений Y. Если каждому
, определена на множестве Х с областью значений Y. Если каждому  соответствует единственное
соответствует единственное  , при котором
, при котором  называется обратной (рис.1.3).
называется обратной (рис.1.3).
 . Это соответствие часто записывают также в виде
. Это соответствие часто записывают также в виде  .
.  следует воспринимать как символ для обозначения обратной функции, а не как
следует воспринимать как символ для обозначения обратной функции, а не как  . Например, для функции
. Например, для функции 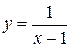 обратной функцией будет
обратной функцией будет  . В полученном выражении поменяем местами х и y, тогда
. В полученном выражении поменяем местами х и y, тогда  – обратная функция.
– обратная функция. ;
;  ;
;  ;
;  .
. ,
, – числа, называемые коэффициентами,
– числа, называемые коэффициентами,  степень многочлена.
степень многочлена. .
. .
. .
. ;
;  .
. ;
;  ;
;  .
.