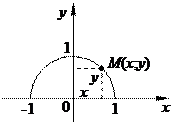|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Область определения и изменения функцииСтр 1 из 3Следующая ⇒
ПРЕДИСЛОВИЕ
Учебное пособие «Основы высшей математики» часть II предназначено для курсантов, обучающихся по специальности «Педагогика и психология». В пособии рассмотрены разделы математического анализа, соответствующие курсу лекций дисциплины «Математика и информатика» (раздел «Математика»), читаемому курсантам I курса в I семестре. Материал пособия удовлетворяет государственному образовательному стандарту для специальности 031000 («Педагогика и психология»). Математика не является основной дисциплиной для этой специальности, однако, данный курс необходим для полноценной подготовки квалифицированных специалистов. Существует множество учебников и сборников задач по математическому анализу, но большинство из них ориентированы на технические специальности. Настоящее учебное пособие позволит курсантам, обучающимся по данной специальности легче адаптироваться к курсу математики. Объем часов, отводимый на изучение дисциплины «Математика и информатика» (раздел «Математика»), сравнительно небольшой, поэтому целью курса является освоение теоретического материала без строгих доказательств и на уровне, достаточном для осмысленного решения задач. Пособие состоит из шести глав, в которых излагаются основы классического математического анализа: функция, предел функции, непрерывность функции, производная и дифференциал функции, исследование функции и построение графиков, неопределенный интеграл. Теоретический курс построен в доступной форме и сопровождается большим количеством пояснительных примеров и рисунков по каждой теме. В конце каждой темы предлагаются упражнения с ответами для аудиторной и самостоятельной работы курсантов. В следующем пособии будут рассмотрены такие темы математического анализа, как определенный интеграл и его приложения, функции нескольких переменных, ряды и дифференциальные уравнения. ГЛАВА 1 ФУНКЦИЯ Переменная величина Изучение каких−либо явлений или процессов в разнообразных областях знаний показывает, что одни величины сохраняют свои значения, другие же принимают различные значения. В математике занимаются величинами, отвлекаясь от их конкретного содержания, а интересуясь прежде всего числовыми значениями, которыми выражаются эти величины. Определение. Переменной величиной называется величина, которая принимает различные числовые значения. Например, в формуле Переменные величины обычно обозначаются последними буквами латинского алфавита: x,y,z,u... Переменная величина х считается заданной, если известно множество значений, которое она может принимать. Это множество называется областью изменения переменной. Определение. Величина, числовые значения которой не меняются, называется постоянной величиной. Примерами таких величин могут служить: скорость света, скорость звука в вакууме, постоянная Планка ( Постоянные величины обозначаются первыми буквами латинского алфавита: а,b,c,... . Замечание. В математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.
Понятие функции Для исследования различных явлений полезно знать, как изменение одних величин влияет на другие величины. Понятие функции связано с установлением зависимости (связи) между двумя (несколькими) переменными величинами при их совместном изменении, или установлением зависимости между элементами двух (нескольких) множеств. Определение. Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению Для указания этого факта, что y есть функция от х, пишут: Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так
Рис. 1.1
Переменная х называется независимой переменной или аргументом. Переменная y называется зависимой переменной или функцией. Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.
Область определения и изменения функции Определение. Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения или областью существования этой функции. Определение. Множество Х называется областью определения функции и обозначается Обычно областью определения функции являются: - отрезок (сегмент или замкнутый промежуток)
- интервал (открытый промежуток)
- полуоткрытые интервалы (полуоткрытые отрезки)
- бесконечные интервалы (промежутки)
где
Например, для функций: 1) 2) Область определения функции может состоять из одного или нескольких промежутков и из отдельных точек. Определение. Множество значений Y называется областью изменения или областью значений функции, и обозначается Область изменения функции (множество ее значений) определяется законом соответствия. Например, для функций 1) 2) Определение. Функция В дальнейшем будем изучать лишь числовые функции. Частное значение функции Например, если Последовательность Определение. Функция, определенная на множестве натуральных чисел Значения функции Последовательность обычно обозначают через Например,
График функции Для наглядного представления функции строят ее график. Определение. Графиком функции Например, графиком функции
Рис. 1.2
Поиск по сайту: |
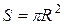 , площадь S круга является величиной переменной, зависящей от радиуса круга R.
, площадь S круга является величиной переменной, зависящей от радиуса круга R. ) и т.д.
) и т.д. ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение  .
.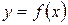 ,
, 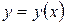 ,
,  и т.п.
и т.п. (рис.1.1).
(рис.1.1).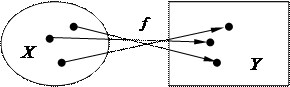
 .
. ;
; ;
; ;
; ;
; ;
; 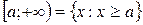 ;
; ;
;  ;
;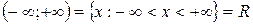 ,
, ,
,  и
и  .
. ;
; .
. .
. ;
;  ;
;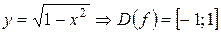 ;
;  .
.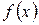 называется числовой функцией, если ее область определения
называется числовой функцией, если ее область определения  записывается так:
записывается так: 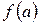 .
.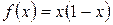 , то
, то 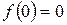 ,
, 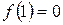 ,
,  и т.п.
и т.п. , называется последовательностью.
, называется последовательностью. т.е. элементы множества
т.е. элементы множества 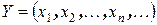 называются членами последовательности, а
называются членами последовательности, а  – общим членом последовательности.
– общим членом последовательности. или
или  ;
;  .
.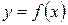 называется множество всех точек плоскости
называется множество всех точек плоскости  , для каждой из которых х является значением аргумента,
, для каждой из которых х является значением аргумента,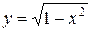 является верхняя полуокружность радиуса
является верхняя полуокружность радиуса  с центром в
с центром в  (рис. 1.2).
(рис. 1.2).