 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример расчёта трехшарнирной арки ⇐ ПредыдущаяСтр 2 из 2
Для сплошной трехшарнирной арки требуется: а) определить аналитически моменты, поперечные и нормальные силы в сечениях К1 и К2 от действия постоянной нагрузки. б) построить линии влияния М, Q и N для сечения К2 и по ним найти значения М, Q и N от той же постоянной нагрузки.
Исходные данные:
Решение: 1. Так как арка очерчена по закону параболы, уравнение оси имеет вид:
где: синус угла наклона касательной к оси арки
косинус угла наклона касательной к оси арки
Определяем геометрические параметры сечения
Определяем геометрические параметры сечения
3. Определяем балочные опорные реакции:
4.Определяем горизонтальные составляющие опорных реакций - распор:
5.Определяем балочные значения поперечной силы и изгибающего момента в заданных сечениях от действия заданной нагрузки
6.Определяем арочные значения поперечной силы, изгибающего момента и нормальной (продольной) силы в заданных сечениях от действия заданной наг-рузки:
7. Построим линию влияния распора: Линия влияния распора повторяет линию влияния балочного изгибающего момента в сечении С, все ординаты которой уменьшены в «f» раз, где f- стрела подъема арки:
8. Построим линии влияния М,Q и N для сечения К2: а) линия влияния арочного момента представляет собой сумму ординат двух линий влияния: линии влияния балочного изгибающего момента в сечении К2 и линии влияния распора Н, все ординаты которой взяты с обратным знаком и увеличены в УK2 раз:
б) линия влияния арочной поперечной силы представляет собой сумму ординат двух линий влияния: линии влияния балочной поперечной силы в сечении К2, все ординаты которой умножены на cos
в) линия влияния арочной продольной силы представляет собой взятую с обратным знаком сумму ординат двух линий влияния: линии влияния балочной поперечной силы в сечении К2, все ординаты которой умножены на sin
9. По линиям влияния определяем значения М,Q и N в сечении К2 от пос-тоянной нагрузки, для этого воспользуемся выражением:
где: S – любое усилие или опорная реакция, Pi – приложенная заданная сосредоточенная сила,
qi – заданная равномерно распределенная нагрузка,
Ординаты линий влияния и площади соответствующих участков опреде-ляем из подобия треугольников, используя в качестве отправных характерные (базовые) ординаты линий
Поиск по сайту: |




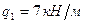











 , где
, где 
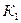 :
: 


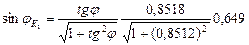

 :
: 

























 , и линии влияния распора Н, все ординаты которой взяты с обратным знаком и умножены на sin
, и линии влияния распора Н, все ординаты которой взяты с обратным знаком и умножены на sin 
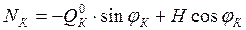
 ;
; - ордината линии влияния, расположенная под точкой приложения силы Рi,
- ордината линии влияния, расположенная под точкой приложения силы Рi, i – площадь участка линии влияния, расположенного подравномерно распределенной нагрузкой.
i – площадь участка линии влияния, расположенного подравномерно распределенной нагрузкой.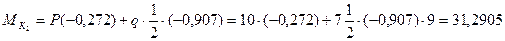 (кН/м)
(кН/м) (кН/м)
(кН/м) (кН/м)
(кН/м)