 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приклади розв’язування задач ⇐ ПредыдущаяСтр 2 из 2
1.Знайдіть канонічний вид кососиметричної форми:
Розв’язання: Нагадаємо, що канонічним видом кососиметричної форми є наступний вигляд:
Приведемо дану форму до необхідного вигляду. Для цього згрупуємо доданки, що містять
Покладемо:
Звідси:
Підставимо (8.3) у (8.2) і зберемо доданки, що містять
Введемо ще одну заміну змінних:
Виразимо з останніх співвідношень
Підставимо вирази (8.5) у (8.4). Тим самим отримаємо канонічний вид кососиметричної форми:
2.Знайдіть значення, при якому квадратична форма додатно визначена:
Розв’язання: Для відповіді на це питання скористаємося критерієм Сильвестра. Складемо матрицю квадратичної форми: Обчислимо значення її головних мінорів:
Очевидно, що при 3.Приведіть квадратичну форму до канонічного виду методом Лагранжа:
Розв’язання: Оскільки
Введемо заміну:
Внаслідок цього квадратична форма набере вигляду:
Підкреслимо доданки з
Останнє дає можливість записати дану квадратичну форму в канонічному виді:
Для отримання лінійного перетворення, що приводить вихідну квадратичну форму до знайденого канонічного виду, необхідно підставити формули (8.7) у (8.6). Отже,
4.Приведіть квадратичну форму до канонічного виду методом ортогональних перетворень:
Розв’язання: Складемо матрицю Грама даної квадратичної форми:
Знайдемо її власні значення (вони будуть коефіцієнтами при квадратах змінних в шуканому канонічному виді):
Звідси Для знаходження перетворення, що приводить дану квадратичну форму до канонічного виду, знайдемо власні вектори, що відповідають знайденим власним значенням. При
Власний вектор, що відповідає власному значенню При
Власні вектори, що відповідають власному значенню Легко перевірити, що Нормуємо знайдені вектори:
Оскільки вони вже попарно ортогональні, то складемо матрицю переходу:
А, отже, лінійне перетворення, що приводить дану квадратичну форму до канонічного виду, можна записати у вигляді системи:
5.Приведіть квадратичну форму до канонічного виду методом Якобі:
Розв’язання: Складемо матрицю Грама і знайдемо її головні мінори:
Тоді 6.Зведіть пару квадратичних форм
до канонічного виду одним лінійним перетворенням. Розв’язання: Перевіримо за критерієм Сільвестра, яка з наведених квадратичних форм додатно визначена. Для цього запишемо їх матриці:
Не важко з’ясувати, що Застосуємо метод Лагранжа до додатно визначеної форми
форма До квадратичної форми
При
Отже, власному значенню При
Фундаментальну систему розв’язків даної системи утворюють вектори:
Таким чином, Нормуємо отримані вектори
та запишемо їх по стовпцях матриці ортогонального перетворення
Тобто перетворенням змінних
квадратична форма Підставимо (8.9) в (8.8) та отримаємо сумарне перетворення
або в скороченому вигляді
що приводить форми Завдання для самостійного розв’язування 1.Нехай 1) 2) 3) 4) 5) 2.Нехай 1) 2) 3) 4) 3.Чи є білінійною функцією на 4.Запишіть матрицю білінійної функції 5.Запишіть матрицю білінійної функції 1) б) 2) а) 3) б) 4) а) 5) б) 6.Запишіть матрицю даної білінійної форми та відповідну їй квадратичну форму в 1) 2) 7.Відновіть симетричну білінійну форму в 1) 8.Зведіть до нормального виду дані квадратичні форми. Визначте їх ранг, додатний та від’ємний індекси інерції та сигнатуру. Які з даних форм додатно визначені, від’ємно визначені або напіввизначені? 1) 2) 3) 4) 5) 6) 9.Знайдіть канонічний вид та одне перетворення координат, що приводить до цього виду, для квадратичних форм над 1) 3) 5) 7) 8) 9) 10.З’ясуйте, які з квадратичних форм 1) 2) 3)
4) 5)
11.Знайдіть всі значення 1) 2) 3) 4) 5) 12.З’ясуйте, що в наступних парах квадратичних форм одна є додатно визначеною; знайдіть не вироджене лінійне перетворення, що приводить цю форму до нормального, а іншу до канонічного виду; запишіть цей канонічний вид: 1) 2) 3) 4) 5) 13.Знайдіть ортогональне перетворення, що приводить наступні квадратичні форми до канонічного виду, запишіть цей вид: 1) 2) 3) 4) 5)
Поиск по сайту: |

 .
. .
.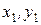 , і винесемо їх за дужки:
, і винесемо їх за дужки:
 . (8.2)
. (8.2)

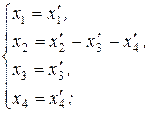
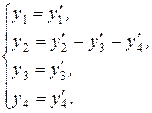 (8.3)
(8.3) :
: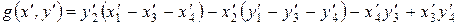 . (8.4)
. (8.4)

 ,
, 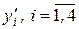 , через
, через  ,
,  :
: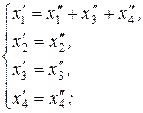
 (8.5)
(8.5) .
.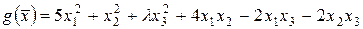 .
.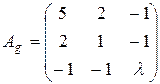 .
. ,
,  ,
,  .
.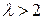 форма буде додатно визначена.
форма буде додатно визначена. .
. , то звернемо увагу на доданки, що містять
, то звернемо увагу на доданки, що містять  (підкреслені):
(підкреслені): .
.
 (8.6)
(8.6)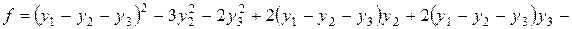
 .
. та застосуємо ще одне перетворення змінних:
та застосуємо ще одне перетворення змінних:
 (8.7)
(8.7)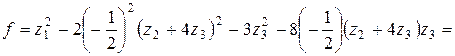
 .
.
 .
. .
. .
. – шуканий канонічний вид даної квадратичної форми.
– шуканий канонічний вид даної квадратичної форми. :
: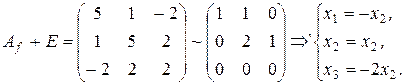
 .
. :
:
 ,
,  .
. , а
, а  . Знайдемо координати вектора
. Знайдемо координати вектора  з умов:
з умов:  . Помножимо скалярно рівність
. Помножимо скалярно рівність  . Отримаємо, що
. Отримаємо, що  . Покладемо
. Покладемо  і одержимо координати вектора
і одержимо координати вектора  .
.
 .
.

 – шуканий канонічний вид.
– шуканий канонічний вид. ,
,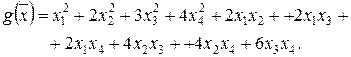
 ,
,  .
. , а
, а  ,
, 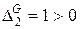 ,
, 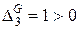 ,
,  . Отже, додатно визначеною виявилася форма
. Отже, додатно визначеною виявилася форма  .
. (8.8)
(8.8) . Застосувавши таке саме перетворення до форми
. Застосувавши таке саме перетворення до форми  , отримаємо
, отримаємо  .
. застосуємо метод ортогональних перетворень. Запишемо матрицю цієї форми та знайдемо її власні значення і відповідні їм власні вектори:
застосуємо метод ортогональних перетворень. Запишемо матрицю цієї форми та знайдемо її власні значення і відповідні їм власні вектори: ,
, ;
;  кратності 1,
кратності 1,  кратності 3.
кратності 3. ;
;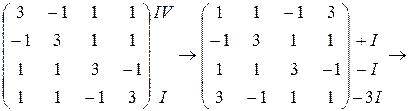


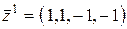 .
. ;
;
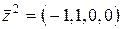 ,
,  ,
,  . Нескладно переконатись, що всі вектори попарно ортогональні, окрім
. Нескладно переконатись, що всі вектори попарно ортогональні, окрім  та
та 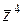 :
:  . Знайдемо новий вектор
. Знайдемо новий вектор 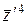 за умови, що
за умови, що  ,
,  ,
,  . Його координати
. Його координати  мають задовольняти системі рівнянь:
мають задовольняти системі рівнянь: ;
;

 .
. ;
; ;
; ;
;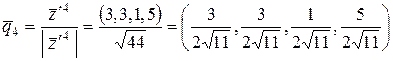
 :
: .
. ,
, (8.9)
(8.9) зводиться до
зводиться до  . При цьому ж перетворенні квадратична форма
. При цьому ж перетворенні квадратична форма  .
.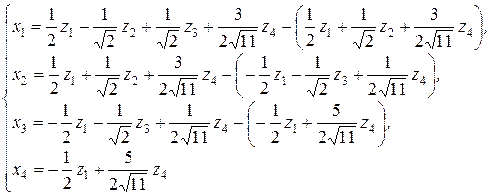
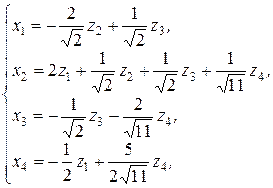
 ,
,  .
. – дійсний лінійний простір. Перевірте, чи є лінійною на
– дійсний лінійний простір. Перевірте, чи є лінійною на  , де
, де  – задані дійсні числа,
– задані дійсні числа,  – координати вектора
– координати вектора 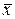 у деякому базисі простору
у деякому базисі простору 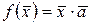 , де
, де  – заданий вектор;
– заданий вектор;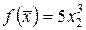 ;
;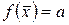 , де
, де  – задане дійсне число;
– задане дійсне число; ,
,  , де
, де  – задана функція з
– задана функція з 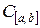 .
. є білінійною симетричною функцією на
є білінійною симетричною функцією на  ;
; ;
; ;
; , де
, де  – симетрична функція.
– симетрична функція.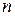 - вимірному просторі
- вимірному просторі  , де
, де  – перші координати векторів
– перші координати векторів  у деякому базисі?
у деякому базисі? в ортонормованому базисі
в ортонормованому базисі 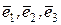 , якщо
, якщо  .
. в заданому базисі дійсного лінійного простору
в заданому базисі дійсного лінійного простору  ;
;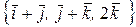 ;
; ,
,  , базис:
, базис: ;
;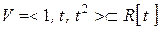 ,
, 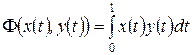 , базис: а)
, базис: а)  ;
; ;
; ,
, 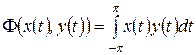 , базис:
, базис: ; б)
; б)  ;
; ,
,  , базис: а)
, базис: а)  ;
; .
. ;
; .
.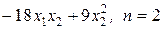 ; 2)
; 2)  .
. ;
; ;
; ;
;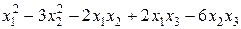 ;
;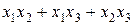 ;
; .
. :
: ; 2)
; 2) 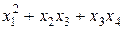 ;
; ; 4)
; 4)  ; 6)
; 6)  ;
;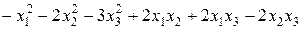 ;
; ;
;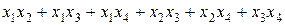 .
.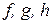 еквівалентні між собою: а) над
еквівалентні між собою: а) над  ; б) над
; б) над  ;
; ;
; ,
, ,
,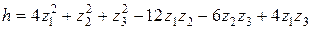 ;
;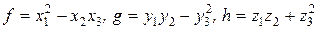 ;
;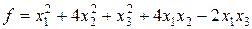 ,
,  ,
, .
. , при яких додатно визначені квадратичні форми:
, при яких додатно визначені квадратичні форми: ;
; ;
; ;
;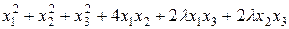 ;
; .
. ;
; ;
; ;
;  ;
; ;
;  ;
; ;
;  .
. ;
; ;
; ;
; ;
;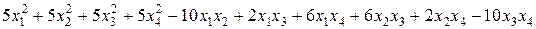 .
.