 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм зведення пари квадратичних формСтр 1 из 2Следующая ⇒
ЛІНІЙНІ, БІЛІНІЙНІ ФУНКЦІОНАЛИ. КВАДРАТИЧНІ ФОРМИ Нехай 1) 2) 3) 4) Білінійний функціонал називається симетричним, якщо виконується умова Білінійний функціонал називається кососиметричним, якщо виконується умова Відображення Іншими словами, квадратичною формою змінних
де Матрицею Грама квадратичної форми в даному базисі називається матриця полярного до неї білінійного функціонала:
Канонічним видом кососиметричної форми є наступний вигляд:
Канонічним видом квадратичної форми називається:
Нормальним видом квадратичної форми називається:
Квадратична форма називається: – додатно визначеною, якщо – від’ємно визначеною, якщо Критерій Сильвестра.Квадратична форма Метод Якобі. Канонічний вид квадратичної форми можна знайти за наступною формулою:
де Метод Лагранжа. Розглянемо квадратичну форму виду (8.1). 1. Якщо 2. Якщо 3. Якщо Таким чином, в результаті скінченого числа перетворень квадратичну форму можна привести до канонічного виду. Метод ортогональних перетвореньзведення квадратичної форми до канонічного виду полягає в наступному: 1. Записати матрицю 2. Визначити з характеристичного рівняння 3. Для кожного власного значення 4. До отриманих власних векторів, що відповідають власному значенню 5. Після того, як будуть знайдені всі 6. Записати канонічний вид квадратичної форми
де 7. Записати лінійне перетворення змінних
яке приводить задану квадратичну форму до канонічного виду. Розглянемо процес ортогоналізації Грама-Шмідтадовільного базису Покладемо
З векторів
Отже
Побудований вектор
Отже
Вектор Таким чином,
Продовжуючи за вказаною схемою процес створення попарно ортогональних векторів Алгоритм зведення пари квадратичних форм
Поиск по сайту: |
 – лінійний простір над полем
– лінійний простір над полем 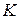 . Відображення
. Відображення 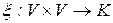 називається білінійним функціоналом над простором
називається білінійним функціоналом над простором 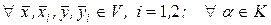 :
: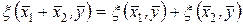 ;
;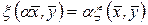 ;
; ;
;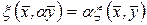 .
. .
. .
. називається квадратичною формою, якщо існує такий симетричний білінійний функціонал
називається квадратичною формою, якщо існує такий симетричний білінійний функціонал 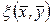 , що
, що 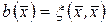 . Білінійний функціонал
. Білінійний функціонал 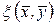 називається полярним до квадратичної форми
називається полярним до квадратичної форми  .
.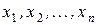 називають функцію вигляду
називають функцію вигляду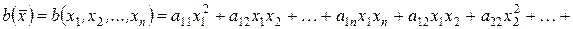
 , (8.1)
, (8.1)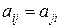 – дійсні або комплексні числа.
– дійсні або комплексні числа.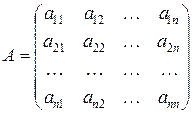 .
. .
.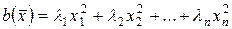 ,
,  ,
, 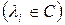 ,
, 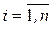 .
. , де
, де 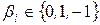 .
.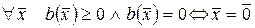 ;
; .
. ,
, – головні мінори матриці
– головні мінори матриці 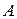 квадратичної форми,
квадратичної форми, 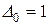 .
.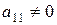 , то покладемо
, то покладемо 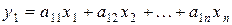 ,
, 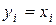 ,
, 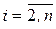 і перетворимо квадратичну форму до вигляду
і перетворимо квадратичну форму до вигляду 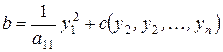 .
.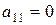 , але
, але 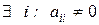 , то, змінюючи нумерацію змінних, приходимо до попереднього випадку.
, то, змінюючи нумерацію змінних, приходимо до попереднього випадку.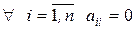 , але
, але 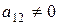 , то покладемо
, то покладемо 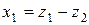 ,
, 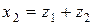 ,
, 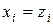 ,
, 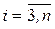 , та приходимо до першого випадку.
, та приходимо до першого випадку. власні значення цієї матриці (всі вони дійсні, оскільки матриця
власні значення цієї матриці (всі вони дійсні, оскільки матриця 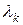 визначити відповідні йому лінійно незалежні власні вектори.
визначити відповідні йому лінійно незалежні власні вектори.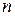 власних векторів матриці
власних векторів матриці 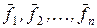 в
в  .
.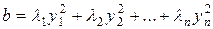 ,
, або
або  ,
,
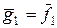 .
. і
і  утворюємо вектор
утворюємо вектор 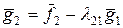 . Число
. Число 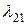 візьмемо таким, щоб
візьмемо таким, щоб  . Маємо:
. Маємо: .
. . Тоді
. Тоді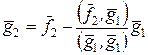 .
.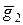 ортогональний вектору
ортогональний вектору 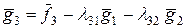 . Підберемо числа
. Підберемо числа  і
і 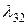 так, щоб
так, щоб  і
і  . Для визначення цих чисел маємо рівняння:
. Для визначення цих чисел маємо рівняння: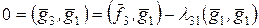 ,
,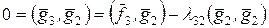 .
.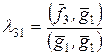 ,
,  . Тоді
. Тоді .
. , очевидно, ортогональний векторам
, очевидно, ортогональний векторам  , де
, де  .
. , побудуємо за скінчене число кроків ортогональний базис
, побудуємо за скінчене число кроків ортогональний базис