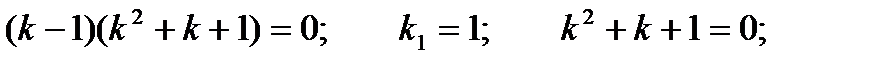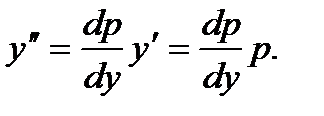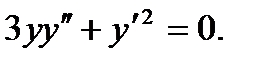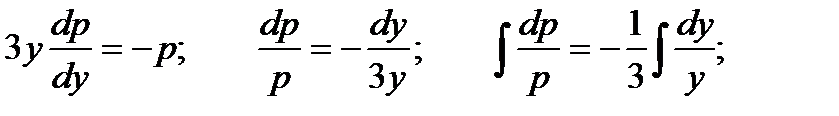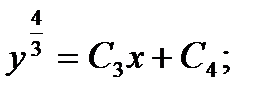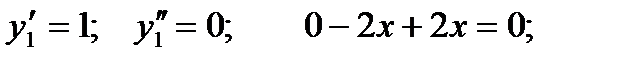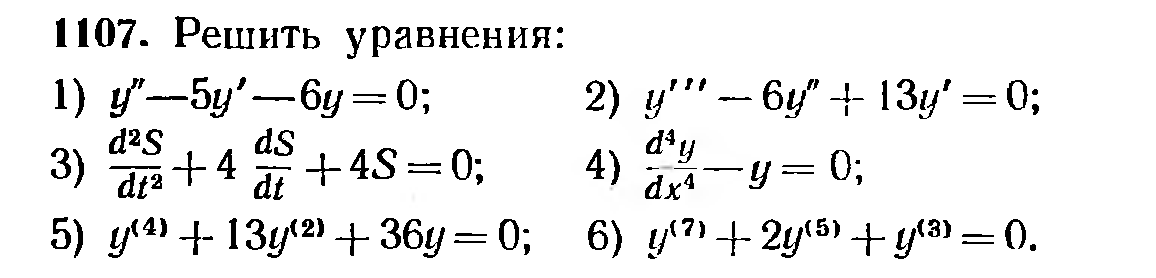|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Решение дифференциального уравнения вида
Т.к.
При этом многочлен Для того чтобы функция
Т.к. ekx ¹ 0, то
Как и любое алгебраическое уравнение степени n, характеристическое уравнение
В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.
Сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.
1) Составляем характеристическое уравнение и находим его корни. 2) Находим частные решения дифференциального уравнения, причем: a) каждому действительному корню соответствует решение ekx; б) каждому действительному корню кратности m ставится в соответствие m решений:
в) каждой паре комплексно – сопряженных корней
г) каждой паре m – кратных комплексно – сопряженных корней
3) Составляем линейную комбинацию найденных решений.
Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами. Пример 1. Решить уравнение Решение.Характеристическое уравнение: Общее решение: Пример 2. Решить уравнение Решение.Характеристическое уравнение: Общее решение:
Пример 3. Решить уравнение Решение.Характеристическое уравнение:
Общее решение:
Пример 4. Решить уравнение Решение.Характеристическое уравнение:
Общее решение:
Пример 5. Решить уравнение Решение.Характеристическое уравнение:
Общее решение:
Пример 6. Решить уравнение Решение.Составим характеристическое уравнение:
Общее решение:
Пример 7. Решить уравнение Решение.Составим характеристическое уравнение:
Общее решение имеет вид: Пример 8. Решить уравнение Решение.Это уравнение не является линейным, следовательно, приведенный выше метод решения к нему неприменим. Понизим порядок уравнения с помощью подстановки Тогда
Окончательно получаем: Это выражение будет общим решением исходного дифференциального уравнения. Полученное выше решение у1 = С1 получается из общего решения при С = 0.
Пример 9. Решить уравнение Решение.Производим замену переменной:
Общее решение:
Пример 10. Решить уравнение Решение.Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение. Таким частным решением будет являться функция
Исходное дифференциальное уравнение можно преобразовать: Общее решение имеет вид:
Окончательно:
Примеры. Решить уравнения:
Примеры. Найти частный интеграл уравнения, удовлетворяющий начальным условиям:
Поиск по сайту: |
 или, короче,
или, короче,  будем искать в виде
будем искать в виде 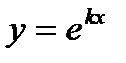 , где k = const.
, где k = const. то
то 
 называется характеристическим многочленомдифференциального уравнения.
называется характеристическим многочленомдифференциального уравнения. т.е.
т.е. 
 - это уравнение называется характеристическим уравнением.
- это уравнение называется характеристическим уравнением. имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения: и
и  .
.



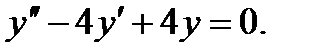
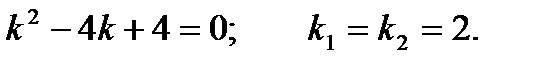
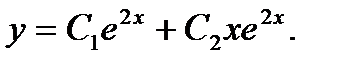



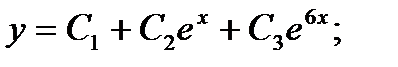
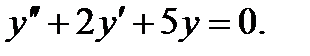
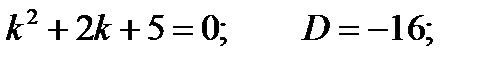

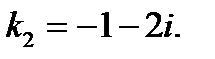
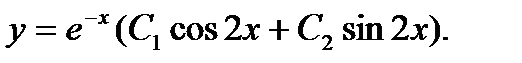





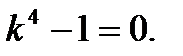


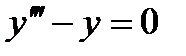 .
.