 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задание 2. Измерение длины волны лазерного излучения. ⇐ ПредыдущаяСтр 3 из 3
Эксперимент 1. Для объекта 27, используя то же оборудование, при максимальном (допускаемом установкой) значении
Рис. 4.5. 2. Выньте объект 27 из двухкоординатного держателя и вставьте его в кассету микропроектора (модуль 2). Отодвиньте объектив на 1,5 – 2 см ближе к конденсору (модуль 5), при этом система расфокусируется, объект 27 в кассете микропроектора окажется освещенным, и на экране установки будет видно увеличенное изображение двух щелей. Измерьте по этому изображению ширину щели D и расстояние между щелями Н. Учитывая увеличение микропроектора, рассчитайте действительную ширину щели 3. Рассчитайте длину волны излучения лазера по формуле: 4. Повторите опыт с объектом 28. 5. Результаты занесите в таблицу:
Сделайте вывод о проделанной работе.
Контрольные вопросы 1. В чем заключается явление интерференции света? 2. Назовите условия получения и наблюдения интерференции света. 3. Запишите условия интерференционного максимума и минимума. 4. Что называется оптической длиной пути? 5. Каков механизм возникновения интерференционной картины в опыте Юнга? 6. Как связаны разность фаз и оптическая разность хода? Пояснить на рисунке.
Ответы на контрольные вопросы: 1. Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. Интерференция является параметром волн а также не зависит ни от параметров среды, ни от ее наличия. 2. Условие получения: волны должны иметь одинаковую частоту и постоянную разность фаз, т.е. волны должны быть когерентными. Источники таких волн будут называться когерентными. Условие наблюдения: необходимо две световые волны, которые при встрече будут давать либо усиление, либо ослабление света, т.е. можно наблюдать чередование светлых и темных полос. 3. Условия интерференционного максимума и минимума: max: min: где λ0 – длина волны излучения в вакууме. В общем случае можно записать:
Параметр 4. Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками. Отрезку луча длиной l в среде с показателем преломления n соответствует оптическая длина L=nl. Для луча, прошедшего от точки A до тоски B:
5. В качестве источников используются две щели, освещаемые излучением лазера. Вследствие дифракции пучки излучения после щелей получаются расходящимися, благодаря чему перекрываются и дают интерференционную картину (рис. 4.3а). Однако, при освещении щелей плоской волной, пучки не успевают пересечься в пределах длины
Рис. 4.3 Поэтому мы освещаем щели сходящейся волной (рис. 4.3.б), полученной с помощью короткофокусной линзы и объектива.
Схема опыта приведена на рис. 4.4. Пучок лазера превращается конденсором Л1 и объективом О в волну, сфокусированную в объектной плоскости Э2 линзы Л2 микропроектора с координатой риски
6. Для двух волн, распространяющихся в разных средах и интерферирующих друг с другом, разность фаз связана с оптической разностью хода соотношением:
где L2 и L1 – «оптические длины» 2-х лучей, идущих от источника до точки наблюдения,
Поиск по сайту: |
 измерьте ширину интерференционной полосы. Для этого разность координат минимумов, разнесенных на несколько полос в пределах центрального дифракционного максимума, разделите на число полос. На рис.4.5 показано измерение на экране Э3 ширины интерференционной полосы:
измерьте ширину интерференционной полосы. Для этого разность координат минимумов, разнесенных на несколько полос в пределах центрального дифракционного максимума, разделите на число полос. На рис.4.5 показано измерение на экране Э3 ширины интерференционной полосы:  , где
, где  и
и 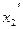 - координаты центров двух темных полос, симметричных относительно центрального максимума,
- координаты центров двух темных полос, симметричных относительно центрального максимума,  - число светлых полос между двумя данными темными,
- число светлых полос между двумя данными темными,  - увеличение микропроектора (на рис. 4.5 N = 3).
- увеличение микропроектора (на рис. 4.5 N = 3).
 и расстояние между щелями
и расстояние между щелями  .
.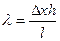 .
.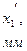






 , k – целое, (4.6)
, k – целое, (4.6) , k – целое, (4.7)
, k – целое, (4.7) . (4.8)
. (4.8) называют порядком интерференции. Целым
называют порядком интерференции. Целым  . (4.5)
. (4.5)

 . При этом на экране установки Э3 видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой
. При этом на экране установки Э3 видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой 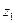 . При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3.
. При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3. ,
,
 и
и  - расстояния (геометрические пути), пройденные соответственно волнами от первого и второго источников до точки наблюдения, где
- расстояния (геометрические пути), пройденные соответственно волнами от первого и второго источников до точки наблюдения, где 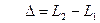 ,
, – длина волны излучения в вакууме.
– длина волны излучения в вакууме.