 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интерференция света: общие сведения.Стр 1 из 3Следующая ⇒
Астраханский Государственный Технический Университет
КАФЕДРА ФИЗИКИ Лабораторная работа №4 по теме: «Изучение интерференции световых волн с помощью щелей Юнга»
Выполнил: студент 2-го курса гр. ДТКК-21б/1 Курбатов Сергей Проверила: доц. кафедры физика Быкова В.П.
Допуск к л.р. _______ Выполнение л.р. _______ Зачтено _______
Астрахань 2014 Лабораторная работа №4 Изучение интерференции световых волн с помощью щелей Юнга Цель работы: проверить основные соотношения теории интерференции, определить длину волны лазерного излучения. Оборудование: модули: микропроектор 2, конденсор 5, объектив 6, кассета в двухкоординатном держателе 8; объекты: щели 23 и 24, пары щелей 27 и 28; лист бумаги.
Краткая теория Интерференция света: общие сведения. Колебания, протекающие согласованно, называют когерентными. Для колебаний, близких к гармоническим, когерентность означает постоянную во времени разность фаз δ. При сложении двух когерентных волн наблюдается явление интерференции, заключающееся в том, что интенсивность I результирующей волны не равна сумме интенсивностей I1 и I2 складываемых волн:
Если разность фаз складываемых колебаний постоянна во времени и равна δ, то
Если I1=I2, то в минимуме Imin= Разность фаз δ определяется оптической разностью хода Δ:
L2 и L1 – «оптические длины» 2-х лучей, идущих от источника до точки наблюдения,
Условия интерференционного максимума и минимума: max: min: где λ0 – длина волны излучения в вакууме. В общем случае можно записать:
Параметр
Две плоские волны с малым углом Ширина полосы (расстояние между соседними минимумами или соседними максимумами):
Волны, пришедшие на экран Э от достаточно удаленных точечных источников
Опыт Юнга. В качестве источников используются две щели, освещаемые излучением лазера. Вследствие дифракции пучки излучения после щелей получаются расходящимися, благодаря чему перекрываются и дают интерференционную картину (рис. 4.3а). Однако, при освещении щелей плоской волной, пучки не успевают пересечься в пределах длины
Рис. 4.3.
Поэтому мы освещаем щели сходящейся волной (рис. 4.3.б), полученной с помощью короткофокусной линзы и объектива. Схема опыта приведена на рис. 4.4. Пучок лазера превращается конденсором Л1 и объективом О в волну, сфокусированную в объектной плоскости Э2 линзы Л2 микропроектора с координатой риски
В схеме на рис. 4.4 и последующих вместо реального положения экрана Э3`, показанного пунктиром, дается положение Э3, в котором игнорируется излом лучей зеркалом микропроектора.
Поиск по сайту: |
 . (4.1)
. (4.1) . Если δ=2kπ (k – целое), то интенсивность максимальна, если δ=(2k+1)π – минимальна. Соответствующие интенсивности равны
. Если δ=2kπ (k – целое), то интенсивность максимальна, если δ=(2k+1)π – минимальна. Соответствующие интенсивности равны , (4.2)
, (4.2) (4.3)
(4.3)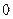 – свет плюс свет дает темноту. Как правило, в разных точках пространства величина δ имеет разные значения, и возникает чередование темных и светлых полос, называемое интерференционной картиной. Расстояние между соседними светлыми или соседними темными полосами (т.е. между соседними максимумами или минимумами интенсивности) называют шириной интерференционной полосы.
– свет плюс свет дает темноту. Как правило, в разных точках пространства величина δ имеет разные значения, и возникает чередование темных и светлых полос, называемое интерференционной картиной. Расстояние между соседними светлыми или соседними темными полосами (т.е. между соседними максимумами или минимумами интенсивности) называют шириной интерференционной полосы. , где
, где 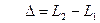 ,
, – длина волны излучения в вакууме. Отрезку луча длиной l в среде с показателем преломления n соответствует оптическая длина L=nl. Для луча, прошедшего от точки A до тоски B:
– длина волны излучения в вакууме. Отрезку луча длиной l в среде с показателем преломления n соответствует оптическая длина L=nl. Для луча, прошедшего от точки A до тоски B: . (4.5)
. (4.5) , k – целое, (4.6)
, k – целое, (4.6) , k – целое, (4.7)
, k – целое, (4.7) . (4.8)
. (4.8) называют порядком интерференции. Целым
называют порядком интерференции. Целым  Рис. 4.1.
Рис. 4.1.
 Рис. 4.2.
Рис. 4.2.
 между направлениями распространения, в плоскости, перпендикулярной среднему направлению распространения, дают интерференционную картину (рис. 4.1) в виде чередующихся темных и светлых полос.
между направлениями распространения, в плоскости, перпендикулярной среднему направлению распространения, дают интерференционную картину (рис. 4.1) в виде чередующихся темных и светлых полос. . (4.9)
. (4.9) и
и  (рис. 4.2), можно в области экрана Э считать плоскими. Очевидно,
(рис. 4.2), можно в области экрана Э считать плоскими. Очевидно, 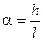 , где h –расстояние между точечными источниками, l – расстояние от плоскости источников до экрана (
, где h –расстояние между точечными источниками, l – расстояние от плоскости источников до экрана ( 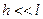 ), соответственно
), соответственно . (4.10)
. (4.10) нашей установки.
нашей установки.
 . При этом на экране установки Э3 видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой
. При этом на экране установки Э3 видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой 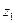 . При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3. Для наблюдения и измерения параметров самих объектов их помещают в кассету в объектной плоскости линзы Э2, а объектив О смещают так, чтобы волна расфокусировалась и осветила всю поверхность объекта. При этом на экране установки Э3 возникает увеличенное изображение объектов.
. При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3. Для наблюдения и измерения параметров самих объектов их помещают в кассету в объектной плоскости линзы Э2, а объектив О смещают так, чтобы волна расфокусировалась и осветила всю поверхность объекта. При этом на экране установки Э3 возникает увеличенное изображение объектов. Рис. 4.4.
Рис. 4.4.