 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связи между динамическими характеристиками ⇐ ПредыдущаяСтр 2 из 2
Передаточная функция системы ® последовательное соединение n звеньев, когда выходная величина предыдущего звена является входной для последующего
® параллельное соединение n звеньев (здесь входная величина одновременно подаётся на входы всех звеньев, а выходная равна сумме выходных величин отдельных звеньев)
® соединение с отрицательной обратной связью (частный случай встречно-параллельного соединения звеньев
® соединение с положительной обратной связью (другой частный случай встречно параллельного соединения)
При решении задач анализа и синтеза автоматических радиоэлектронных устройств широко используется частотные характеристики – амплитудно-фазовая частотная характеристика (АФЧХ), амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). Это объясняется тем, что многие сигналы в радиосхемах представляют в виде суммы гармонических сигналов, возможностью экспериментального определения частотных характеристик и удобством их использования при рассмотрении структурных схем САУ, исследовании устойчивости и других свойств системы. АФЧХ или комплексная частотная характеристикам W(jω) определяется как отношение преобразования Фурье F выхода системы
К преобразованию Фурье входа
Т.е.
Здесь w – угловая частота; Сигналы на входе и выходе можно записать в виде
Тогда
Где
Здесь M(ω) есть АЧХ; (ω)-ФЧХ; P(ω) – действительная (вещественная) частотная характеристика; Q(ω) – мнимая частотная характеристика. Временные характеристики системы представляют собой реакции системы на стандартные входные воздействия: ® единичная ступенчатая функция
® дельта-функция или единичная импульса функция
Вывод: После проделанной работы я усовершенствовал свои навыки по вводу текста, формул, таблиц. Для ввода формул и таблиц пользовался меню «Вставка», далее «Таблица» или «Формула».
Поиск по сайту: |
















 находится по передаточным функциям
находится по передаточным функциям  её элементарных звеньев с использованием следующих формул:
её элементарных звеньев с использованием следующих формул: (1.3)
(1.3) (1.4)
(1.4) , когда на вход соединения одновременно с входной величиной x системы, подаётся её выходная величина, прошедшая через звено обратной связи с передаточной функцией
, когда на вход соединения одновременно с входной величиной x системы, подаётся её выходная величина, прошедшая через звено обратной связи с передаточной функцией  :
: (1.5)
(1.5) (1.6)
(1.6)

 ; (1.7)
; (1.7) - односторонние функции, т. е. y(t)-0, x(t)-0 при t<0.
- односторонние функции, т. е. y(t)-0, x(t)-0 при t<0.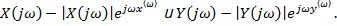
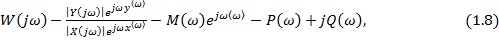

 (1.9)
(1.9)
