 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Идентификация модели объекта управленияСтр 1 из 2Следующая ⇒
При анализе линейных систем различают переходные и установившиеся процессы. Свойства систем и их элементов (звеньев) для этих процессов определяются динамическими и статистическими характеристиками. В общем случае статическая характеристика (СХ) для системы с сосредоточенными параметрами с одним входом и одним выходом представляет собой зависимость выходной переменной у от значения входной переменной х в установившемся режиме и записывается в форме алгебраического уравнения Где X-область значения х. Уравнение (1.1) называется уравнением статики. Для объектов с m входами статическая характеристика записывается в виде функции у от нескольких входных переменных, т. е.
В случае линейной системы с одним входом и одним выходом СХ (1.1) записывается как уравнение прямой линии Для линейной системы с m входами статическая характеристика имеет вид
а для многомерной системы с m входами и m выходами СХ записывается как система линейных уравнений
…………………………………………………………
Звенья САУ, имеющие СХ, называют статическими звеньями, а объекты управления – объектами с самовыравниванием. Знание статической характеристики объекта управления необходимо для выбора режимов работы, определения области, в пределах которой объект можно считать линейным, расчёта функций чувствительности к изменению входных переменных и т. д. Для системы, состоящей из n последовательно соединённых линейных звеньев со статическими характеристиками
Когда выход одного звена является входом другого
При этом передаточный коэффициент К системы равен произведению передаточных коэффициентов звеньев, т. е.
Передаточный коэффициент системы при параллельном соединении звеньев, когда
Равен сумме значений В случае соединения звеньев по схеме отрицательной обратной связи, когда управление u пропорционально разности между заданным значением
Статическая характеристика замкнутой САУ имеет вид
Где Следует заметить, что при описании статической характеристики звена важно указать диапазон значений изменения x, при котором зависимость выхода у от х можно считать линейной, а для статической характеристики САУ следует указать диапазоны линейности, входящих в её звенья. Некоторые звенья (системы, объекты) не имеют СХ. Например, если у электродвигателя в качестве выходной величины у рассматривать угол поворота якоря, а в качестве входной х –подводимое напряжение, то при Свойства объекта, САУ и отдельных её звеньев в переходных процессах (динамических режимах) определяют с помощью динамических характеристик (ДХ). В зависимости от свойств системы и решаемых задач анализ и синтеза для описания переходных процессов в САУ используется дифференциальные уравнения, передаточные функции, частотные и временные характеристики. Основные задачи, решаемые с использование различных ДХ применительно к непрерывным САУ, приведены в табл. 1.1. Дифференциальные уравнения (ДУ) наиболее часто используются в качестве моделей динамических режимов как объектов управления, так и САУ. По известному ДУ можно получить любые другие ДХ системы. Так, для определения временных характеристик необходимо решить ДУ при соответствующем входном сигнале, передаточная функция находится с использованием преобразования Лапласа, а амплитудиофазочастотная характеристика – преобразована Фурье. Обычно ДХ составляет основу математической модели исследуемой системы.
Поиск по сайту: |
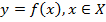 (1.1)
(1.1)
 ; здесь
; здесь 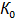 ,
, 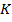 – постоянные коэффициенты; коэффициенты К называют передаточным или коэффициентом усиления.
– постоянные коэффициенты; коэффициенты К называют передаточным или коэффициентом усиления.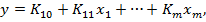
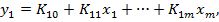
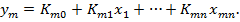
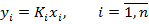
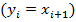 , CХ всей системы со входом
, CХ всей системы со входом 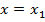 и выходом
и выходом 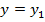 имеет аналогичный вид, т. е.
имеет аналогичный вид, т. е.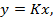
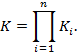
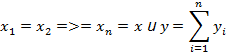
 .
.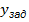 и y, т. е.
и y, т. е.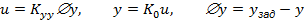
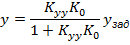
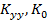 – передаточные коэффициенты управляющего устройства и объекта, соответственно.
– передаточные коэффициенты управляющего устройства и объекта, соответственно.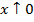 установившегося значения у не наступает. Такие звенья называют астатическими звеньями, а объекты – объектами без самовыравнивания.
установившегося значения у не наступает. Такие звенья называют астатическими звеньями, а объекты – объектами без самовыравнивания.