 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Порядок виконання роботи. МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИСтр 1 из 4Следующая ⇒
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Харкiвський НАЦІОНАЛЬНИЙ унiверситет
Ф.М. АНДРЄЄВ МЕТРОЛОГІЯ І ВИМІРЮВАННЯ Керiвництво до лабораторних робiт Харкiв УДК 621.03.01 Керiвництво до лабораторних робiт з навчальної дисциплiни "Метрологія і вимірювання" складене вiдповiдно до типової навчальної програми i включає опис лабораторних робiт з усiх роздiлiв дисциплiни. Керiвництво до лабораторних робiт розглянуто i рекомендовано до опублiкування на засiданнi кафедри електроніки та управляючих систем 18 грудня 2009 року, протокол № 13.
ПЕРЕДМОВА В данiй методичнiй розробцi приводяться опис i методика виконання лабораторних робiт з навчальної дисциплiни "Метрологія і вимірювання". Лабораторний практикум з дисципліни "Метрологія і вимірювання" проводиться з метою: поглиблення знань, які отримані на лекціях та при самостійної роботи над дисципліною; отримання практичних навичок з застосування засобів вимірювань, а також з статистичної обробки та оформлення результатів вимірювань. Опис лабораторних робiт утримає : мету та програму роботи; короткі відомості з теорії; методичні вказівки до підготовки та виконання роботи, рекомендації до оформлення роботи; контрольні питання. Короткі відомості з теорії дозволяють полегшувати підготовку студентів до виконання робіт. Обсяг матеріалу з теорії є мінімальний для проведення потрібних досліджень, ізмерітельного експерименту і отримання необхідних результатів. Контрольні питання, які наведені в конці опису роботи, призначені для самоперевірки та проведення колоквіуму перед роботами. У ходi виконання лабораторних робiт студенти повиннi керуватися правилами роботи в лабораторiї, знати й суворо дотримуватися правил з технiки безпеки.
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОРИСТАННЯ ПЕОМ
1. На D диску відкрити папку «Андреев Лаб. работы». 2. Запустить програму “mc7demo.exe”. 3. У вікні “Tip of Day» натиснути кнопку “Close». 4. Натиснути кнопки “File”, а потім “Open”. ЛАБОРАТОРНАЯ РОБОТА № 1
«ДОСЛІДЖЕННЯ МЕТОДІВ ПЕРЕВІРКИ ГИПОТЕЗ ПРО ВИД ЩІЛЬНОСТНОСТІІ ЙМОВІРНОСТІ РЕЗУЛЬТАТІВ ВИМІРЮВАНЬ»
1. Мета роботи Дослідження методів перевірки гипотез про вид щільності ймовірності результатів вимірювань. Програма роботи 2.1 Вивчення методів перевірки гипотез про вид щільності ймовірності результатів вимірювань; 2.2. Дослідження особливостей використання цих методів в метрології. 2.3. Отримання практичних навичок з статистичної обробки результатів багаторазових вимірювань при перевірки гипотез про вид щільності ймовірности результатів вимірювань.
3. Підготовка до виконання роботи 3.1. За конспектом лекцiй вивчити матерiали підроздiлу 3.5 «Перевірка гіпотези про вид функції щільності ймовірности результатів вимірювань». 3.2. Вивчити: мету та програму роботи; форми представлення та оформлення результатів досліджень. 3.3. Підготувати бланк звіту: записати мету та програму роботи, основні співвідношення, намалювати таблиці. 3.4. Перевірити ступень готовності до лабораторної роботи по контрольним питанням, які надруковані в кінці опису даної роботи.
4. Короткі відомості з теорії У найпростішому випадку вид функції щільності ймовірностіможна встановити по виду гістограми, побудованої за результатами багаторазових вимірювань, але вона дає досить грубе уявлення про закон щільності розподілу. Тому частіше висловлюється гіпотеза про те, що результати вимірювань ФВ можна вважати реалізаціями випадкової величини з певною формою функції щільності розподілу. Відомо декілька так званих критеріїв згоди, за допомогою яких перевіряються гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу ймовірностей. Найбільш розповсюдженим з них критерій
4.1. Критерій c2 (хі-квадрат) Критерій
де
Значення Теоретична величина
Щільність ймовірності цієї величини:
де Г(∙) – відома гама-функція. Інтегральна функція
Рис.3.6. Функція
Гіпотеза про нормальність розподілу результатів спостережень приймається, якщо виконується нерівність
Методика застосування критерію 1. Для серії n результатів спостережень 2. Визначають дослідні значення частостей
Таблиця 3.1. – Рекомендації щодо вибору числа інтервалів
Ширину інтервалу h визначають за формулою
Для кожного інтервалу гістограми підраховують число 3. Розраховують теоретичні ймовірності Імовірності
де Для визначення числа
Для кожного значення
4. За одержаними значеннями справедливість гіпотези за критерієм
Складений критерій
Складений критерій використовується при перевірці гіпотези про нормальність розподілу вибірки результатів спостережень, якщо 15≤n≤50. Він включає 2 незалежні критерії: критерій I забезпечує перевірку відповідності поблизу центра розподілу; критерій II - на краях розподілу. Якщо одночасно здійснюються ці критерії, приймається гіпотеза про нормальність розподілу результатів спостережень. Для кожного з двох критеріїв задається свій рівень значущості - Критерій I . Розраховується співвідношення
Гіпотеза про нормальність розподілу за критерієм I підтверджується, якщо виконується нерівність
де За критерієм II гіпотеза про нормальність розподілу підтверджується, якщо не більше ніж m різниць
Критерій W Перевірка згоди експериментального та нормального розподілу при 10<n<50 здійснюється за допомогою критерію W. Методика його застосування: 1. Результати спостережень Хq розміщують у варіаційний ряд Хmin= 2. Заносять вихідні дані в таблицю 3.2 В ніжної частині стовбцю 3 табл. 3.2 записують значення j від одиниці до
З використанням даних табл. 3.2 розраховують параметри
та показник
Згідно з заданим рівнем значущості результатів спостережень Критерії згоди лише дозволяють перевірити, чи допустимо щільність ймовірності одержаних результатів спостережень віднести до відомого виду розподілу, здебільшого до нормального.
Порядок виконання роботи. 5.1. Перелічити методи, які використовуються в метрології для перевірки гипотез про вид щільності ймовірності результатів вимірювань;
5.2. Записати результати досліджень особливостей використання хі-квадрат,складеного та W критеріїв в метрології. 5.3. Досліджувати особливості методики розрахунків та отримати практичні навички з використання складного критерію. Для цього здійснити перевірку згоди експериментального розподілу на відповідність нормальному закону по складному критерію для вихідних даних, які наведені в таблиці 5.1. Таблиця 5.1. – Вихідні дані.
В табл.. 5.1 буква N позначає номер студента в журналі групи. Згідно з п.4.2 методика розрахунку з використанням складеного критерію передбачає: 1. Розрахунок 2. Визначення математичного сподівання 3. Оцінка відхилень ∆Хі = 4. Визначення суми відхилень 5. Розрахунки значень квадратів відхилень 6. Визначення суми квадратів відхилень 7. Розрахунок зміщеної оцінки середньо квадратичного відхилення (СКВ) 8. Визначення параметру
9. Знаходження квантилей розподілу для довірчої ймовірності РД = 0,95 з таблиць додатку 10 в кінці опису роботи в вигляду d1-0,5 10. Перевірка виконання першого з критеріїв (критерия І) d1-0,5 11. Розрахунок незміщеної оцінки середньо квадратичного відхилення 12. Знаходження значень P2, які відповідають різним значенням n та q2= α = 0,05 з таблиць додатку 11 в кінці опису роботи, що потрібні для знаходження значень квантиля Z 13. Знаходження значень квантиля Z 14. Визначення граничного значення відхилень ∆ГР = Z 15. Перевірка виконання другого критерію (критерия ІІ) 16. Прийняття рішення.
5.4. Досліджувати особливості методики розрахунків та отримати практичні навички з використання W критерію. Для цього здійснити перевірку згоди експериментального розподілу на відповідність нормальному закону по W критерію для вихідних даних, які наведені в таблиці 5.2. Таблиця 5.2. – Вихідні дані.
В табл.. 5.2 буква N позначає номер студента в журналі групи. Згідно з п.4.3 методика розрахунку з використанням W критерію передбачає: 1. Визначення 2. Розрахунок ( 3. Визначення 4. Визначення 5. Результати розрахунків в п.п. 1…4 дозволяють визначити параметр φ2, який є знаменником для W критерію φ2 =
Наступні операції дозволяють визначити чисельник b2 для W критерію .
6. Визначення з таблиць додатку 12 для існуючого об’єму виборці n = 15 значень коефіцієнтів 7. Розрахунок значень різниць Х16-j - Xj та занесення їх в колонку 5 табл. 5.2: для j = 1 значення Х16-j - Xj = Х15 - X1 - в графу 15 колонки 5, для j = 2 - значення Х16-j - Xj = Х14 - X2 - в графу 14 колонки 5 і т.д. 8. Обчислення добутків а16-j ∙ (Х16-j - Xj) та занесення їх в колонку 6 таблиці 5.2. 9. Оцінка суми добутків ∑ а16-j ∙ (Х16-j - Xj) та занесення ії в графу ∑ колонки 6 таблиці 5.2. 10. Визначення чисельнику b2 для W критерію b2 = [∑ а16-j ∙ (Х16-j - Xj)]2 . 11. Оцінка експериментального значення критерію W W = 12. Для заданого рівня значущості результатів спостережень α2 = 0,05 знаходження табличного значення W* (додаток 13 в кінці опису роботи). 13. Прийняття рішення.
Змiст звiту 6.1. Мета i програма роботи. 6.2. Результати досліджень особливостей використання існуючих в метрології методов встановлення виду функції щільності ймовірності. 6.3.Результати дослiджень у виглядi таблиць та результатів розрахункiв. 6.4. Висновки вiдносно результатiв виконаної роботи: перевірки згоди експериментального розподілу на відповідність нормальному закону за складним критерієм; перевірки згоди експериментального розподілу на відповідність нормальному закону за W критерієм.
7. Контрольнi запитання 7.1.Які існують методи встановлення виду функції щільності ймовірності? 7.2. Які в метрології існують критерії згоди, за допомогою яких перевіряються гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу? 7.3. При яких об’ємах вибірок результатів вимірювань використовуються існуючи в метрології критерії згоди, за допомогою яких перевіряються гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу? 7.4. Запишіть вираз для зміщеної оцінки середньо квадратичного відхилення (СКВ) . 7.5. Запишіть вираз для незміщеної оцінки середньо квадратичного відхилення (СКВ) . 7.6. Запишіть вираз для оцінки математичного сподівання при рівноточних вимірюваннях. 7.7. Надати визначення квантиля будь – якого розподілу. 7.8. Сутність поняття «довірча ймовірність». 7.9. Запишіть вираз для першого з критеріїв (критерия І) при використанні складеного критерію для перевірки гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу. 7.10. Запишіть вираз для другого з критеріїв (критерия ІІ) при використанні складеного критерію для перевірки гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу. 7.11. Запишіть вираз для W критерію при перевірки гіпотези про відповідність експериментальних даних теоретичної функції щільності розподілу.
ДОДАТОК 6
Поиск по сайту: |
 , а також складений та W критерії.
, а також складений та W критерії. використовується для перевірки узгодженості теоретичного та експериментального розподілів різних видів при числі результатів вимірювань у серії (спостережень) n≥50. Сутність його: оцінка відхилення гістограми експериментальних даних від гістограми з тим самим числом інтервалів, побудованої на основі теоретичного розподілу. Для кожного інтервалу гістограми визначають значення теоретичної і дослідної частостей (кількості спостережень, що потрапляють у даний інтервал) і знаходять показник різниці частостей. Величина
використовується для перевірки узгодженості теоретичного та експериментального розподілів різних видів при числі результатів вимірювань у серії (спостережень) n≥50. Сутність його: оцінка відхилення гістограми експериментальних даних від гістограми з тим самим числом інтервалів, побудованої на основі теоретичного розподілу. Для кожного інтервалу гістограми визначають значення теоретичної і дослідної частостей (кількості спостережень, що потрапляють у даний інтервал) і знаходять показник різниці частостей. Величина  (3.23)
(3.23)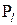 - теоретична ймовірність попадання результатів спостережень у l-й інтервал гістограми;
- теоретична ймовірність попадання результатів спостережень у l-й інтервал гістограми; 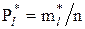 - дослідна (статистична) оцінка ймовірності (частість) попадання результатів спостережень у l-й інтервал,
- дослідна (статистична) оцінка ймовірності (частість) попадання результатів спостережень у l-й інтервал,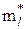 - експериментальне (дослідне) число результатів спостережень, що попадають у l-й інтервал гістограми;
- експериментальне (дослідне) число результатів спостережень, що попадають у l-й інтервал гістограми;  - теоретичне (очікуване) число результатів у l-му інтервалі; r - число інтервалів гістограми з постійною шириною h.
- теоретичне (очікуване) число результатів у l-му інтервалі; r - число інтервалів гістограми з постійною шириною h. ) і числа степенів вільності
) і числа степенів вільності  , де s - число незалежних зв’язків, накладених на частості
, де s - число незалежних зв’язків, накладених на частості 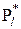 . Якщо перевіряється гіпотеза про нормальний розподіл, то до останніх належать: по-перше, рівності середнього арифметичного математичному сподіванню, а також точкової оцінки дисперсії і дисперсії передбачуваного нормального розподілу; по-друге, рівність одиниці суми частостей усіх інтервалів, тобто
. Якщо перевіряється гіпотеза про нормальний розподіл, то до останніх належать: по-перше, рівності середнього арифметичного математичному сподіванню, а також точкової оцінки дисперсії і дисперсії передбачуваного нормального розподілу; по-друге, рівність одиниці суми частостей усіх інтервалів, тобто  ;
;  ∙
∙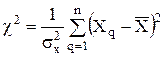 .
.
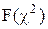 ‑ табульована (додаток 8). Вхідними даними таблиць, які складені, є рівень значущості
‑ табульована (додаток 8). Вхідними даними таблиць, які складені, є рівень значущості  (або довірча ймовірність
(або довірча ймовірність  ) і число степенів вільності
) і число степенів вільності  знаходять нижню
знаходять нижню  і для рівня значущості
і для рівня значущості  - верхню
- верхню  границі критичної області значень
границі критичної області значень 
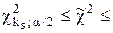
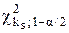 . (3.24)
. (3.24) обчислюють середнє арифметичне і незміщену оцінку СКВ за формулами (3.19) і (3.22) відповідно.
обчислюють середнє арифметичне і незміщену оцінку СКВ за формулами (3.19) і (3.22) відповідно.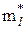 . Для цього результати спостережень Хq розміщують у варіаційний ряд (у порядку зростання) Хmin=
. Для цього результати спостережень Хq розміщують у варіаційний ряд (у порядку зростання) Хmin=  =Хmax і здійснюють групування даних, тобто він розбивається на r рівних інтервалів. Вибір числа r інтервалів проводиться залежно від числа спостережень, що входять у серію. В табл. 3.1. наведена одна з рекомендації щодо такого вибору.
=Хmax і здійснюють групування даних, тобто він розбивається на r рівних інтервалів. Вибір числа r інтервалів проводиться залежно від числа спостережень, що входять у серію. В табл. 3.1. наведена одна з рекомендації щодо такого вибору.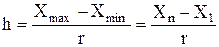 .
. результатів спостережень для кожного з інтервалів.
результатів спостережень для кожного з інтервалів. на його ширину:
на його ширину: ,
, .
. :
: .
. і обчислюють
і обчислюють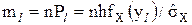 .
. ) обчислюють значення показника
) обчислюють значення показника  із співвідношення (3.23). За таблицею (додаток 9) знаходять граничні значення
із співвідношення (3.23). За таблицею (додаток 9) знаходять граничні значення  та
та  , причому вони повинні задовольняти умову
, причому вони повинні задовольняти умову 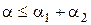 , де
, де 
 - оцінка СКВ результатів спостережень за формулою (3.22), де використовується n замість n-1.
- оцінка СКВ результатів спостережень за формулою (3.22), де використовується n замість n-1. , (3.25)
, (3.25) - квантилі розподілу значень показника d, які знаходять за таблицями значень
- квантилі розподілу значень показника d, які знаходять за таблицями значень  .
. перевищили значення добутку
перевищили значення добутку  , де
, де 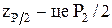 - відсотковий квантиль нормованої інтегральної функції
- відсотковий квантиль нормованої інтегральної функції 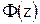 (3.15). При цьому довірча ймовірність
(3.15). При цьому довірча ймовірність  є функцією n і
є функцією n і 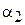 , тобто
, тобто 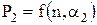 . Значення
. Значення  і m знаходять за таблицею (додаток 11). При цьому для завдання числа m досить однієї координати - кількості спостережень n: при 10<n<20 приймають
і m знаходять за таблицею (додаток 11). При цьому для завдання числа m досить однієї координати - кількості спостережень n: при 10<n<20 приймають 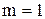 , при
, при 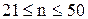 беруть
беруть  . Для завдання значення
. Для завдання значення  (звичайно 1, 2 або 5 %).
(звичайно 1, 2 або 5 %). , де
, де  (додаток 12). При цьому вхідні дані – це значення j та число результатів спостережень n. Наприклад, при j=2; n=15;
(додаток 12). При цьому вхідні дані – це значення j та число результатів спостережень n. Наприклад, при j=2; n=15;  = 0,3306. Потім для кожного значення розраховують різниці
= 0,3306. Потім для кожного значення розраховують різниці  і записують в відповідні рідкі табл. 3.2. В стовпчик 6 вносять результати рядкового перемножування даних стовбців 4 та 5.
і записують в відповідні рідкі табл. 3.2. В стовпчик 6 вносять результати рядкового перемножування даних стовбців 4 та 5.
 Таблиця3.2 –Розрахункові дані
Таблиця3.2 –Розрахункові дані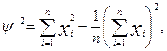 (3.26)
(3.26)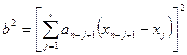
 . (3.28)
. (3.28)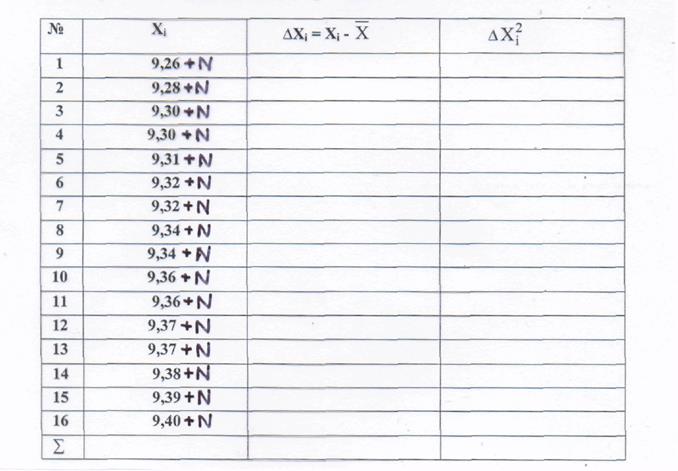
 та занесення в графу ∑ колонки 2 таблиці 5.1.
та занесення в графу ∑ колонки 2 таблиці 5.1. за виразом
за виразом 
 .
. і занесення результату в графу ∑ колонки 3 таблиці 5.1.
і занесення результату в графу ∑ колонки 3 таблиці 5.1.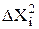 занесення результатів в відповідні графи колонки 4 таблиці 5.1.
занесення результатів в відповідні графи колонки 4 таблиці 5.1. і занесення результату в графу ∑ колонки 4 таблиці 5.1.
і занесення результату в графу ∑ колонки 4 таблиці 5.1. .
. складеного критерію
складеного критерію .
. та d1-0,5
та d1-0,5  .
.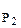 розподілу Ф(Z) .
розподілу Ф(Z) . .
.
 та занесення в графу ∑ колонки 2 таблиці 5.2.
та занесення в графу ∑ колонки 2 таблиці 5.2.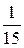 (
( 
 та занесення в відповідну графу колонки 7 табл. 5.2.
та занесення в відповідну графу колонки 7 табл. 5.2. та занесення в графу ∑ колонки 7 таблиці 5.2.
та занесення в графу ∑ колонки 7 таблиці 5.2. .
.