 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Способы задания функций. Замена переменных
В Maple имеется несколько способов представления функции. Способ 1. Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например: > f:=sin(x)+cos(x);
Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при > x:=Pi/4;
> f;
После выполнения этих команд переменная х имеет заданное значение Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs({x1=a1, x2=a2,…, },f),где в фигурных скобках указываются переменные хi и их новые значения аi(i=1,2,…), которые следует подставить в функцию f. Например: > f:=x*exp(-t);
> subs({x=2,t=1},f);
Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, > evalf(%); .7357588824 Здесь использован символ (%) для вызова предыдущей команды. Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом: > f:=(x,y)->sin(x+y);
Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции: > f(Pi/2,0); Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например: > f:=unapply(x^2+y^2,x,y);
Ø f(-7,5);
В Maple имеется возможность определения неэлементарных функций вида
посредством команды > piecewise(cond_1,f1, cond_2, f2, …). Например, функция
записывается следующим образом: > f:=piecewise(x<0, 0, 0<=x and x<1, x, x>=1, sin(x));
Задание 4. Не забудьте, что выполнение всех последующих заданий должно начинаться с текстовой строки, содержащей «Задание №», где № – номер задания. Также помните, что для правильности вычислений перед выполнением каждого пункта задания следует выполнять команду restart. Перед выполнением контрольных заданий следует набирать в текстовом режиме «Контрольные задания». Эти правила оформления относятся ко всем лабораторным работам. 1. Определите функцию > f:=sqrt(1-x^2-y^2);
> f:=subs({x=rho*cos(phi),y=rho*sin(phi)},f);
> f:=simplify(%);
2. Определите функцию > f:=piecewise(x<-1, x, -1<=x and x<1, -x^2, x>=1, -x);
> %+x: simplify(%);
§5. Решение уравнений
Поиск по сайту: |

 , то следует записать:
, то следует записать: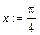

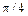 .
.

 и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t),где expr – выражение,t – точность, выраженная в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно:
и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t),где expr – выражение,t – точность, выраженная в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно: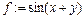




 и перейдите в ней к полярным координатам
и перейдите в ней к полярным координатам  ,
,  . Упростите полученное выражение. Для этого наберите:
. Упростите полученное выражение. Для этого наберите:

 и прибавьте к ней х. Для этого наберите:
и прибавьте к ней х. Для этого наберите:
