 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициент линейной корреляции (метод Пирсона) ⇐ ПредыдущаяСтр 2 из 2
Коэффициент корреляции с использованием для вычисления его отклонения d каждой вариаты V от средней М этого ряда рассчитывается в простых вариационных рядах X и Y по формуле:
d = V – М Средняя ошибка коэффициентов корреляции равна: Величина коэффициента корреляции считается достоверной, если он не менее чем в 3 раза превышает свою среднюю ошибку: Коэффициент корреляции rXY дает возможность вычислить коэффициент регрессии RXY – степень изменения величины одного признака – X при соответствующем изменении другого – Y и наоборот по формуле: Коэффициент регрессии используется в статистике физического развития населения для составления оценочных таблиц. Задания для самостоятельной работы Задача 1. Определите направление и размер корреляционной связи между фактором (условием его действия) и результатом, если известно Показатели «исчерпывающей» заболеваемости работников химических производств с учетом класса болезней, возраста и пола (на 1000 лиц соответствующей группы).
Рассчитайте коэффициенты Пирсона и Спирмена, оцените их достоверность. Задача 2. Определите направление и размер корреляционной связи между фактором (условием его действия) и результатом, если известно Причины смерти работников химических производств с учетом профессиональных особенностей (на 100000 работающих соответствующей группы).
Рассчитайте коэффициенты Пирсона и Спирмена, оцените их достоверность. Задача 3. Определить направление и размер связи между среднемесячной температурой воздуха и числом умерших детей до 1 года от кишечных заболеваний.
Задача 4. Определить направление и размер связи между возрастом матери и количеством сцеженного или высосанного молока из одной груди при шестом кормлении (Метод Пирсона).
Задача 5. Определить наличие корреляции между температурой воздуха и заболеваемостью острыми респираторными заболеваниями среди рабочих цеха N. Было установлено, что со снижением t0 воздуха (Х) увеличилось число заболеваний (У).
Для определения уровня зависимости между этими явлениями требуется рассчитать коэффициент корреляции методом квадратов (метод Пирсона). Задача 6. Определить наличие связи между заболеваемостью населения гепатитом В и охватом прививками лиц, проживающих в разных районах города В (метод Спирмена).
Задача 7. Определить характер и силу связи между возрастом и весом студентов, используя данные, приведенные в таблице (метод Пирсона).
Задача 8. На основании приведенных в таблице данных определите зависимость между пораженностью населения кариесом зубов и содержанием фтора в питьевой воде в некоторых районах N-ской области путем вычисления коэффициента ранговой корреляции (метод Пирсона).
Контрольные вопросы 1. Какие виды связи существуют? 2. Как различается по форме корреляционная связь? 3. Назовите метод, позволяющий измерить величину и направление связи между количественными распределениями? 4. Когда используется коэффициент ранговой корреляции? 5. Назовите этапы расчета коэффициента ранговой корреляции? 6. Что характеризует коэффициент ранговой корреляции, и какие значения он может принимать? 7. Какова методика расчета коэффициента корреляции при альтернативном распределении?
Поиск по сайту: |
 , где n – число парных чисел в корреляционных рядах (групп вариант).
, где n – число парных чисел в корреляционных рядах (групп вариант).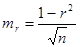
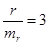 и более.
и более.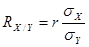 и наоборот
и наоборот 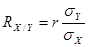 ; σX и σY – средние квадратические отклонения вариационного ряда X и Y.
; σX и σY – средние квадратические отклонения вариационного ряда X и Y.