 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициенты корреляцииСтр 1 из 2Следующая ⇒
Тема: Измерение связи между явлениями или признаками. Корреляция. Цель занятия: Ознакомить студентов с видами взаимосвязи между признаками. Изучить методические основы вычисления и применения коэффициентов корреляции. План занятия: I. Рассмотрение теоретических основ вычисления и использования коэффициентов корреляции. 1. Виды связи между явлениями. 2. Формы корреляционной связи. 3. Характеристика направления и силы связи при корреляционной зависимости. 4. Методика вычисления, область применения и оценка достоверности коэффициента линейной корреляции. 5. Методика вычисления, область применения и оценка достоверности коэффициента ранговой корреляции. 6. Методика вычисления коэффициента корреляции при альтернативном распределении. II. Вычисление коэффициентов корреляции, оценка их достоверности. Основные понятия и определения по теме Все явления в природе и в обществе находятся во взаимной связи. Каждый специалист в результате своей деятельности определяет наличие связи изучаемых явлений, их материальную природу, ее направленность (прямая и обратная), вид связи. Различают две формы (вида) связи: 1) функциональная связь – имеет строгую зависимость явлений, чем больше радиус, тем больше длина окружности (2pR) и эта зависимость проявляется в каждом конкретном случае: изменение одного признака (явления) вызывает обязательно строго определенные изменения другого признака (явления), часто установлена их взаимосвязь математически; 2) корреляционная связь – не имеет строгой зависимости и не проявляется в каждом конкретном случае, а только при массовом сопоставлении изучаемых явлений. Такой вид связи характерен для социально-гигиенических процессов, клинической медицины и биологии. Например, вес человека зависит в основном от его роста, но влияют также на вес и другие факторы: питание, затраты сил на работу, состояние здоровья. Поэтому у лиц одинакового роста, обычно вес варьируется в определенных пределах. В свою очередь корреляционная связь может быть: – прямолинейной, когда отмечается относительно равномерное изменение средних значений одного признака при равных изменениях другого (соответствие между изменениями систолического и диастолического давления); – криволинейной, когда при равномерном изменении одного признака могут наблюдаться возрастающие или убывающие значения другого признака. Кроме того, связь между признаками различается по направлению. Так, когда изменение одного явления ведет к изменению другого явления в том же направлении, (рост экономической обеспеченности ведет к улучшению питания населения) отмечается прямая (положительная) связь и наоборот, когда явления изменяются в разных направлениях (снижение заболеваемости полиомиелитом при увеличении числа привитых) говорят об обратной (отрицательной) связи. Закономерность корреляционной связи пробивается через случайность при массовых наблюдениях. И изучается она статистическими методами – вычислением коэффициентов корреляции. Таблица 1 Схема оценки характера и силы корреляционной связи
Коэффициенты корреляции Коэффициент корреляции рангов (Спирмена) r (ро) – рассчитывается по формуле: где 6 – постоянный коэффициент, n – число коррелируемых пар, d – разность рангов (между порядковыми номерами рядов), Σ – знак суммы. Условиями использования коэффициента ранговой корреляции являются: 1) небольшое число коррелируемых пар; 2) нет необходимости в точных результатах; 3) признаки имеют не только количественные, но и атрибутивные значения (описательные). Методика вычисления коэффициента ранговой корреляции: I этап – присвоение рангов (порядковых номеров) по каждому ряду числовых значений признака. При наличии нескольких одинаковых значений изучаемого признака, ранги присваиваются одни и те же и соответствуют они средней их порядковых номеров. II этап – вычисление разности между рангами в каждой паре коррелируемых признаков. III этап – рассчитывается квадрат разности рангов и определяется их сумма. IV этап – рассчитывают коэффициент ранговой корреляции. Пример: Измерение корреляции между смертностью от рака молочной железы и от рака шейки матки методом рангов (на 100000 женщин в 5 районах). Таблица 2 Матрица расчета коэффициента ранговой корреляции Спирмена (ρ)
При присвоении рангов (в примере от большей смертности к меньшей) при одинаковых величинах явления в ряду, ранги берутся в среднем из суммы их очередных порядковых номеров. Так 19,1 – 1 ранг, 16,0 – 2-ой, следующий тоже 16,0 – 3-ий, так как значения одинаковые, берем: (2+3)/2=5/2=2,5 и каждому одинаковому уровню присваиваются одинаковые ранги равные среднему значению. В нашем примере – 2,5. По выше приведенной формуле вычисляем коэффициент рангов: Для определения достоверности коэффициента корреляции рангов вычисляется его ошибка по формуле:
Достоверность коэффициента корреляции рангов определяется по формуле:
Доверительный коэффициент t должен быть равен или больше 3, что соответствует вероятности 99%, то есть корреляционная связь существенна, если t меньше 3-х – несущественна. При числе наблюдений n<9 существенность полученного коэффициента рангов оценивается по таблице (В.Ю. Урбаха). (Приведена в сокращенном виде). Таблица 3 Критические значения коэффициента корреляции рангов (ρ)
Если число наблюдений (n) равно 9 и более существенность полученного коэффициента можно оценивать по таблице t-критерия (Стьюдента) для числа степеней свободы n' = n – 2, t определяется по вышеприведенной или по следующей формуле:
Вывод. В рассматриваемом примере при n=5, t=2, ρ=-0,8 нельзя утверждать, что между смертностью от рака молочной железы и смертностью от рака шейки матки существует какая-то зависимость, так как ρ=-0,8 меньше критического уровня =0,94 при n=5 по таблице В.Ю. Урбаха и t=2 меньше 3-х.
Поиск по сайту: |
 ,
, r=-0,8
r=-0,8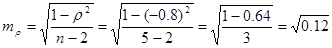 mρ»±0,4
mρ»±0,4
 ;
;