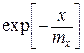|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчет точечных характеристик распределения
Для сгруппированных данных статистические числовые характеристики выражаются приведенными ниже формулами. Статистическое среднее математическое ожидание определяется как
где k – число интервалов группирования случайной величины. Статистическая средняя дисперсия является характеристикой рассеивания случайной величины – разбросанности ее значений около математического ожидания, и определяется по формуле:
После объединения двух первых интервалов в табл. 2, число интервалов k = 4 (см. табл. 3), а значения
Таблица 4
Статистическое среднее математическое ожидание, рассчитанное по формуле (3) составляет Дисперсия Статистические среднее квадратическое отклонение и коэффициент вариации случайной величины составляют:
Величина коэффициента вариации весьма близка к единице, что характерно для экспоненциального закона распределения. Центральные моменты рассчитываются по формуле
Центральные моменты 3-го и 4-го порядков:
Рассчитаем также другие часто применяемые числовые характеристики случайных величин - асимметрию и эксцесс. Асимметрия Sk :
Для симметричных распределений Sk = 0. Четвертый центральный момент служит для характеристики крутости распределения и описывается с помощью эксцесса:
5. Гистограммы и определение закона распределения
Для наглядного представления об эмпирическом распределении строится гистограмма (ступенчатая диаграмма) эмпирической плотности распределения случайной величины (рис. 1). По оси абсцисс откладываются интервалы (разряды) В данном случае вид теоретической функции распределения случайной величины заранее не известен. Основой для подбора той или иной теоретической дифференциальной функции (плотности) распределения, служит внешний вид гистограммы. Сопоставив гистограмму, построенную по данным табл. 3 (рис. 1), с теоретическими кривыми распределения, можно предположить, что анализируемая случайная величина подчиняется экспоненциальному закону распределения.
Рис. 1. Ступенчатая диаграмма эмпирической плотности вероятности Экспоненциальный закон характеризуется плотностью распределения вида
где Рассчитанные значения плотности распределения на границах интервалов сведены в табл. 5. Таблица 5
На гистограмме (рис. 2) по данным табл. 5 построена выравнивающая кривая распределения, представляющая собой график теоретической функции f(t), которая, сохраняя в основном существенные особенности статистического распределения, свободна от случайных неправильностей хода гистограммы.
Рис. 2. Гистограмма (1) и выравнивающая кривая (2) экспоненциального распределения
Поиск по сайту: |
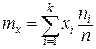 , (3)
, (3)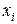 - середины интервалов
- середины интервалов 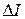 ,
,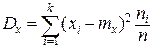 . (4)
. (4)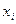 =
= 
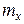 =0,1376.
=0,1376.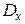 =0,0196.
=0,0196.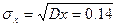 ,
, 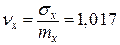
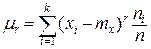 .
.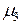 = -0,0044,
= -0,0044, 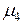 = 0,0016.
= 0,0016.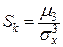 , Sk = 0,0016.
, Sk = 0,0016. ,
, 

 ,
,