 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение частоты и плотности вероятностиСтр 1 из 3Следующая ⇒
Обработка результатов наблюдений о надежности МАШИН Цель работы:получить навыки статистическая обработка информации о надежности и анализа данных наблюдений за работой изделия (наработок на отказ или наработок до отказа). Исходные данные к выполнению задания
Исходными данными к выполнению варианта задания являются следующие эмпирические данные, полученные в результате наблюдений о надежности объекта (табл. 1). Таблица 1 Исходные данные
Первичная обработка данных Определение показателей надежности связано с решением двух главных задач математической статистики — оценки неизвестных параметров выборки и проверки статистических гипотез. Обработка результатов исследований надежности позволяет вычислить числовые характеристики эмпирического распределения (выборки), называемые статистическими оценками (эмпирическими или выборочными характеристиками), которые аналогичны числовым характеристикам случайных величин: математическое ожидание, дисперсия, начальные и центральные моменты различных порядков. При больших объемах выборок n вычисление характеристик затрудняется, поэтому полученные эмпирические данные представляют в виде статистического ряда. Для этого весь диапазон значений случайной величины разбивают на интервалы, число которых в зависимости от объема выборки должно быть не менее 5 - 6 и не более 10 - 12. Примерная величина интервала
где Рекомендуемое число интервалов k группирования случайной величины находится из выражения
Интервалы имеют при этом одинаковую длину. Число значений На основании данных об эмпирическом распределении формируем статистический ряд, используя приведенные формулы. Рассматриваемый ряд состоит из 56 значений случайной величины, минимальным из которых является значение 1,01, максимальным 1,65.
По формуле (1) находим примерную величину интервала
При
Определение частоты и плотности вероятности Для каждого интервала подсчитываем: Накопленная частота Таблица 2
Как видно из табл. 2, в последние четыре интервала попало менее пяти значений случайной величины, поэтому их следует объединить, тогда в объединенном интервале будет содержаться 7 значений (табл. 3). На основании данных табл. 3 могут быть найдены статистические оценки математического ожидания и дисперсии, а также другие характеристики случайной величины. Таблица 3
Поиск по сайту: |
 определяется по формуле:
определяется по формуле: , (1)
, (1) 
 - соответственно максимальное и минимальное значения исследуемой случайной величины; n - количество полученных реализаций случайной величины (объем выборки).
- соответственно максимальное и минимальное значения исследуемой случайной величины; n - количество полученных реализаций случайной величины (объем выборки). . (2)
. (2) случайной величины X в каждом интервале должно быть не менее 5.
случайной величины X в каждом интервале должно быть не менее 5.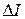 :
:
 ,т.е. k = 7.
,т.е. k = 7. - накопленную частоту;
- накопленную частоту; 
