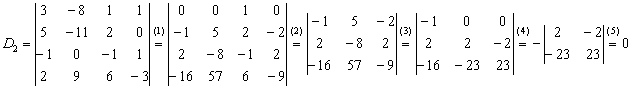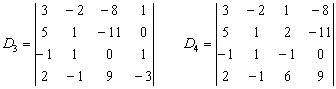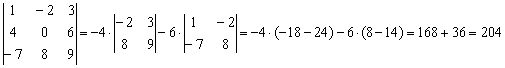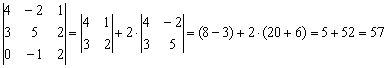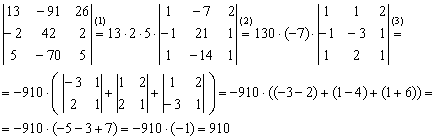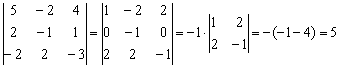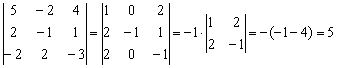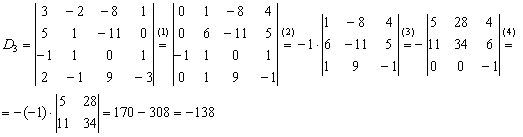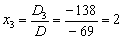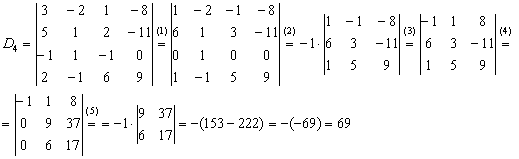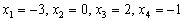|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится ⇐ ПредыдущаяСтр 4 из 4
Возьмём за лапки животное Результат запишем в первый столбец: И, наконец, в определителе Результат помещаем во второй столбец: При элементарном преобразовании меняется ТОТ столбец, к которому прибавляЮТ. Постарайтесь качественно переварить нижеследующий пример. Отправим в суп подросшее земноводное: Задача состоит в том, чтобы с помощью элементарных преобразований понизить порядок определителя до второго порядка. С чего начать? Сначала в определителе нужно выбрать число-«мишень». В качестве «мишени» почти всегда выступает единица либо –1. Смотрим на определитель и замечаем, что здесь даже выбор есть. Пусть числом-«мишенью» будет элемент Примечание: смысл двойных подстрочных индексов можно узнать в статье Правило Крамера. Матричный метод. В данном случае индексы элемента Идея состоит в том, чтобы получить два нуля в третьем столбце: Либо получить два нуля во второй строке: Во второй строке числа поменьше (не забываем золотое правило), поэтому выгоднее взять именно её. А третий столбец с числом-«мишенью» останется неизменным: Ко второму столбцу прибавляем третий столбец: Тут и умножать ничего не пришлось. Результат записываем во второй столбец: К первому столбцу прибавляем третий столбец, умноженный (мысленно) на –2: Как мы понизили порядок определителя? Получили два нуля во второй строке. Решим пример вторым способом, организуем нули в третьем столбце: Вторая строка с числом-«мишенью» останется неизменной: К первой строке прибавим вторую строку, умноженную (мысленно) на –4: Результат записываем в первую строку: К третьей строке прибавим вторую строку, умноженную (мысленно) на 3 (смотрим и считаем снизу вверх): Результат записываем в третью строку, определитель раскрываем по третьему столбцу: Заметьте, что нет никакой необходимости переставлять строки или столбцы. Элементарные преобразования прекрасно работают как слева направо, так и справа налево. Как сверху вниз, так и снизу вверх. Задание 4 Вычислить тот же определитель Это пример для самостоятельного решения. Полное решение и краткие комментарии в конце урока. Иногда в определителе отсутствует единица либо –1, например: Результат записываем в первую строку: ! Внимание: НЕ НУЖНО из первой строки вычитать вторую строку, это значительно увеличивает вероятность ошибки. Только складываем! Поэтому к первой строке прибавляем вторую строку, умноженную –1. Именно так! Единица получена, чего и требовалось достичь. Далее можно получить два нуля в первой строке либо в первом столбце. Желающие могут довести решение до конца (верный ответ: –176). Стоит отметить, что готовая «мишень» чаще всего присутствует в исходном определителе, а уж для определителя 4-го порядка и выше дополнительное преобразование крайне маловероятно. Порубим на гуляш несколько крупных жаб: Задача Решить систему линейных уравнений по формулам Крамера Ничего страшного, если вы ещё не успели ознакомиться с методом Крамера, в этом случае можно просто посмотреть, как понижается порядок у определителя «четыре на четыре». Да и само правило станет понятно, если чуть-чуть вникнуть в ход решения. Решение: сначала вычислим главный определитель системы: Есть возможность пойти стандартным путём, разложив данный определитель по строке либо столбцу. Вспоминая алгоритм первого урока, и, используя придуманную мной матрицу знаков Не вижу вашего энтузиазма =) Безусловно, можно посидеть минут десять и аккуратно-внимательно родить правильный ответ. Но беда в том, что в дальнейшем предстоит вычислить ещё 4 определителя четвёртого порядка. Поэтому единственный разумный выход – понизить порядок определителя. Единиц в определителе много, и наша задача выбрать лучший вариант. Вспоминаем золотое правило: в строке (столбце) нулей должно быть побольше, и числа – поменьше. По этой причине вполне подходит вторая строка либо четвёртый столбец. Четвёртый столбец выглядит привлекательнее, причём, там есть две единицы. В качестве «мишени» выбираем элемент Первая строка не изменится. И вторая тоже – там уже необходимый ноль: К третьей строке прибавим первую строку, умноженную на –1 (смотрим и считаем снизу вверх): ! Внимание ещё раз: Не нужно из третьей строки вычитать первую строку. Только складываем! Результат записываем в третью строку: К четвёртой строке прибавим первую строку, умноженную на 3 (смотрим и считаем снизу вверх): Результат записываем в четвёртую строку: (1) Раскрываем определитель по четвёртому столбцу. Не забываем, что к элементу (2) Порядок определителя понижен до 3-его. В принципе, его можно разложить по строке (столбцу), но лучше отработаем свойства определителя. Вносим минус во вторую строку. (3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 7. (4) Раскрываем определитель по второму столбцу, тем самым ещё понижая его порядок до двух. Заметьте, как сократилось решение! Главное, немного «набить руку» на элементарных преобразованиях, и такая возможность представится прямо сейчас. К тому же в вашем распоряжении есть калькулятор, который считает определители (в частности, его можно найти на странице Математические формулы и таблицы). С помощью калькулятора легко контролировать выполняемые действия. Получили определитель Итак, Вычислим определитель Появился ещё один ноль и очень вкусно выглядит третья строка. При этом в качестве «мишени» выгоднее выбрать элемент Тут даже умножать ничего не надо: Решаем дальше: (1) Раскрываем определитель по третьей строке. Порядок определителя понижен до трёх. (2) Вносим «минус» в первый столбец. (3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 5. (4) Раскрываем определитель по второму столбцу, понижая порядок определителя до двух. По формулам Крамера: Вычислим определитель Так получается, что в рассматриваемых определителях у нас есть нули, в произвольной же задаче их может и не быть. Поэтому для разнообразия оставим нули в покое и раскроем определитель не очень выгодным способом. Выберем элемент Поехали: (2) Раскрываем определитель по первой строке. Порядок определителя понижен до трёх. (3) Ко второму столбцу прибавим первый столбец, умноженный на 5. К третьему столбцу прибавим первый столбец, умноженный на –2. (4) Раскрываем определитель по первой строке. Порядок определителя понижен до двух. (5) Столбцы определителя пропорциональны, значит, он равен нулю. По формулам Крамера: Задание 5 Самостоятельно вычислить определители Концовка решения и ответ на дне страницы. Ваш путь решения может отличаться от моего пути решения, важно, чтобы совпали ответы. Выбор строки или столбца для преобразований нередко обусловлен не только числами, но и удобством решения с субъективной точки зрения. Кому-то удобнее решать по строкам, а кому-то по столбцам. У чайников особенно популярен выбор «мишени» в первой строке, поскольку процесс будет напоминать метод Гаусса. Замечательный получается у нас комплексный обед, и пришло время десерта: Это уже даже не жаба, это сам Годзилла. Возьмём заготовленный стакан апельсинового сока и посмотрим, как понижается порядок определителя. Алгоритм, думаю, понятен: с пятого порядка понижаем до четвёртого, с четвёртого – до третьего и с третьего – до второго:
(1) К первой, третьей, четвертой и пятой строкам прибавим вторую строку. (2) Раскрываем определитель по 3-ему столбцу. Порядок определителя понизился до 4-х. (3) Из 4-го столбца выносим 2. Первую строку умножаем на –1, и чтобы определитель не изменился, ставим перед ним «минус». Данное преобразование выполнено в целях упростить дальнейшие вычисления. (4) Ко второй и третьей строкам прибавим первую строку. К четвертой строке прибавим первую строку, умноженную на 3. (5) Раскрываем определитель по 4-му столбцу. Порядок понижен до трёх. (6) Раскрываем определитель по 2-му столбцу. Порядок понижен до двух. (7) Выносим «минус» из 1-го столбца. Всё вышло проще, чем казалось, у всех монстров есть слабые места! Неутомимые читатели могут попробовать решить определитель пятого порядка каким-нибудь другим способом, благо, единиц в нём тьма. Задание 1:Решение: Задание 2:Решение: определитель выгоднее вычислить по третьей строке: Задание 3:Решение: (1) Из первой строки вынесли 13, из второй строки вынесли 2, из третьей строки вынесли 5. Задание 4:Решение: Понизим порядок определителя, получив нули во второй строке: Понизим порядок определителя, получив нули во втором столбце: Задание 5:Решение: Ответ:
Поиск по сайту: |
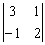 и, используя данное преобразование, получим ноль слева вверху. Для этого мысленно либо на черновике умножим второй столбец на –3:
и, используя данное преобразование, получим ноль слева вверху. Для этого мысленно либо на черновике умножим второй столбец на –3: 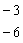 ик первому столбцу прибавим второй столбец, умноженный на –3:
ик первому столбцу прибавим второй столбец, умноженный на –3: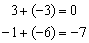
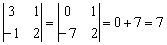



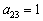 :
: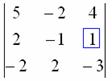
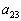 говорят нам о том, что он располагается во второй строке, третьем столбце.
говорят нам о том, что он располагается во второй строке, третьем столбце.

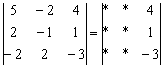


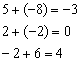
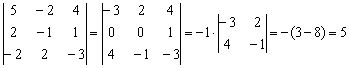
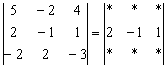


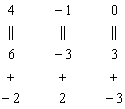
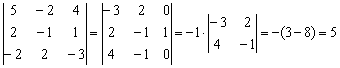
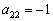 . Понизить его порядок двумя способами: получив нули во второй строке и получив нули во втором столбце.
. Понизить его порядок двумя способами: получив нули во второй строке и получив нули во втором столбце. . В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно чаще всего несколькими способами. Например: к первой строке прибавим вторую строку, умноженную –1:
. В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно чаще всего несколькими способами. Например: к первой строке прибавим вторую строку, умноженную –1:

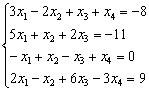

 , раскроем определитель, например, по «классической» первой строке:
, раскроем определитель, например, по «классической» первой строке: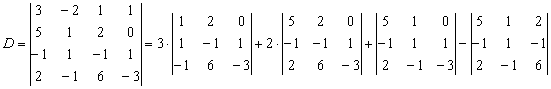
 :
:

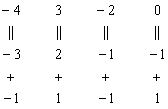
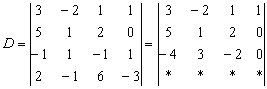
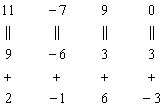
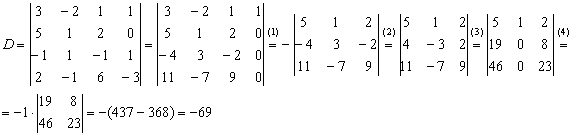
 на первом шаге – и сразу проверили, равен ли он исходному определителю.
на первом шаге – и сразу проверили, равен ли он исходному определителю. , значит, система имеет единственное решение.
, значит, система имеет единственное решение. .
.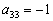 , получив нули в третьей строке:
, получив нули в третьей строке: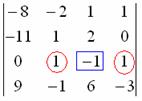
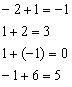 .
. 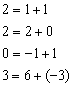 (смотрим и считаем справа налево)
(смотрим и считаем справа налево)
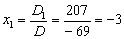
 .
. и получим нули в первой строке:
и получим нули в первой строке: