 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эффективные методы вычисления определителяСтр 1 из 4Следующая ⇒
Свойства определителя. Понижение порядка определителя На втором уроке мы узнаем основные свойства определителя, а также научимся приёмам их эффективного вычисления. Если вы слабо ориентируетесь в теме, пожалуйста, начните с одной из древнейших статей сайта – Как вычислить определитель? Она поможет не только чайникам, но даже тем, кто впервые услышал слово «определитель». Минуло два года с тех пор, когда на сайте было всего десять страничек, и вот, после моего долгого-долгого путешествия в мир матана, всё возвращается на круги своя. Представьте, что вам нужно вычислить определитель третьего порядка, разложив его по элементам строки (столбца). Хотя чего тут представлять – нужно же =) Над ним можно сидеть 5 минут, а можно 2-3 минуты. Или даже в районе одной минуты. Время, которое вы потратите, зависит не только от вашего опыта, но и от знаний свойств определителей. Не редкость, когда процесс решения вполне реально сократить до считанных секунд, а иногда и сразу увидеть результат! «Ерунда, чего экономить на спичках, и так всё решим», – скажут некоторые. Допустим. И не допустим оплошностей ;-) Но как быть с достаточно распространённым на практике определителем 4-го порядка? Воевать с этим перцем придётся уже 10-20 минут. И это будет даже не бой, а бойня, поскольку очень велика вероятность вычислительной ошибки, которая «завернёт» вас на второй круг решения. А если определитель пятого порядка? Спасёт только понижение порядка определителя. Да, такие примеры тоже встречаются в контрольных работах. Материалы данной страницы позволят значительно улучшить вашу технику решения определителей и упростят дальнейшее освоение высшей математики. Эффективные методы вычисления определителя В первую очередь коснёмся не свойств определителя, а как раз методов его рационального вычисления. Эти приёмы решения лежат на поверхности и понятны многим, но всё-таки остановимся на них подробнее. Предполагается, что читатель уже умеет достаточно уверенно раскрывать определитель третьего порядка. Как известно, данный определитель можно раскрыть 6-ю стандартными способами: по любой строке или любому столбцу. Казалось бы, без разницы, ведь ответ получится один и тот же. Но все ли способы одинаково легкИ? Нет. В большинстве случаев есть менее выгодные пути иболее выгодные пути решения. Рассмотрим определитель Разложим определитель по второму столбцу: На практике нулевые элементы игнорируются, и запись решения принимает более компактный вид: Задание 1 Раскройте данный определитель по второй строке, используя укороченную запись. Решение в конце урока. Если в строке (либо столбце) два нуля, то это вообще настоящий подарок. Рассмотрим определитель
Вот и всё решение! Особый случай, когда определитель имеет так называемый ступенчатый илитреугольный вид, например: Разложим его по первому столбцу: В практических заданиях удобно руководствоваться следующим правилом – ступенчатый определитель равен произведению чисел его главной диагонали: Аналогичный принцип справедлив и для ступенчатых определителей других порядков, например: Треугольные определители появляются в некоторых задачах линейной алгебры, и их решение чаще всего оформляют именно так. А если в строке (столбце) определителя находятся одни нули? Ответ, думаю, понятен. Мы ещё вернёмся к этому вопросу в свойствах определителя. Теперь представим, что долгожданные баранки не положены в новогодний подарок. Так давайте же распотрошим нехорошего Санта-Клауса!
Здесь нет нулей, но всё равно существует способ облегчить себе жизнь. Данный определитель оптимальнее разложить по третьему столбцу, поскольку там самые маленькие числа. При этом запись решения принимает весьма лаконичный вид: Резюмируя параграф, сформулируем золотое правило вычислений: Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где: 1) нулей побольше; Естественно, это справедливо и для определителей высших порядков. Небольшой пример для закрепления материала: Задание 2 Вычислить определитель, раскрыв его по строке либо столбцу, используя при этом наиболее рациональный способ
Это пример для самостоятельного решения, оптимальное решение и ответ – в конце урока. И ещё один важный совет: не комплексуйте! Не нужно «зацикливаться» на традиционном разложении по первой строке либо первому столбцу. Как короче – так и решайте! Свойства определителя Насчитывается порядка десяти свойств определителя (смотрите учебники, справочники), однако реальное прикладное значение имеют только некоторые из них. И сейчас я попытаюсь в подробной и доступной форме поделиться практическим опытом использования данных свойств. Рассмотрим старых знакомых первого урока: матрицу На всякий случай повторю элементарное различие между понятиями: матрица – это таблица элементов, аопределитель – это число.
Поиск по сайту: |
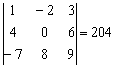 , который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!
, который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!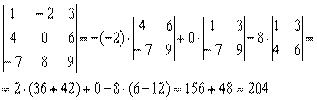
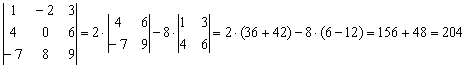
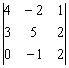
 . Здесь два нуля в третьей строке, по ней и раскрываем:
. Здесь два нуля в третьей строке, по ней и раскрываем: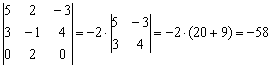
 – в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.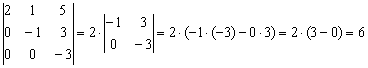
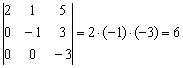
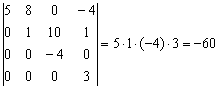

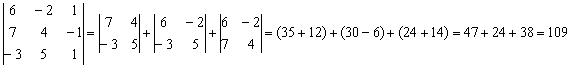
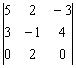
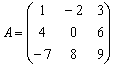 и её определитель
и её определитель 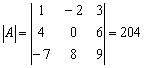 .
.