 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. 1. Измерить радиус круговой или длину стороны квадратной рамки.
1. Измерить радиус круговой или длину стороны квадратной рамки. 2. Собрать схему (рис.6). 3. Установить плоскость рамки в плоскости магнитного меридиана (стрелка компаса должна стоять параллельно виткам рамки и указывать на 0о). 4. Включить источник тока. Увеличивая ток в катушке, добиться отклонения стрелки магнита на 30о. Записать значение тока. 5. Изменить направление тока и повторить измерение тока при отклонении стрелки на 30о в противоположную сторону. 6. Проделать аналогичные действия, отклоняя стрелку компаса вправо и влево на 450 и 600. Пользуясь измеренными значениями, рассчитать величину H0 по одной из формул (14) или (15). Результаты измерений усреднить, вычислить (H0). 7. По классу точности амперметра kI найти значение абсолютной погрешности определения силы тока ΔI: 8. Рассчитать погрешности измерений. Результаты измерений и вычислений занести в таблицу.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Чем обусловлено существование магнитного поля тока? 2. Какие величины характеризуют силовое действие магнитного поля? 3. Как связаны между собой напряженность и индукция магнитного поля? 4. В каких единицах измеряется напряженность, индукция магнитного поля? 5. Как определить направление вектора индукции магнитного поля элемента проводника с током? круговой рамки? 6. Какие величины связывает закон Био-Савара, для чего он служит? 7. Какими основными параметрами характеризуется магнитное поле Земли? 8. В чем сущность метода определения горизонтальной составляющей магнитного поля Земли? 9. Используя закон Био-Савара, получите выражение для индукции магнитного поля круговой рамки с током. 10. Как устроен тангенс гальванометр и каково его назначение в этой работе?
ЛАБОРАТОРНАЯ РАБОТА № 1.4 ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА Цель работы: ознакомление с действием магнитной силы, освоение одного из методов определения удельного заряда частицы. Приборы и принадлежности: магнетрон, источник питания, амперметр, вольтметр, миллиамперметр. ОСНОВНЫЕ ПОЛОЖЕНИЯ Студент должен знать: силу, действующую со стороны магнитного поля на движущийся заряд; как устроен и работает ламповый диод; как движется электрон под действием электрического поля лампы в отсутствие и при наличии внешнего магнитного поля. На заряд q, движущийся в магнитном поле, действует сила, которую будем называть магнитной. Лоренц опытным путем установил, что эта сила определяется выражением: Модуль силы Лоренца (магнитной силы) Направлена магнитная сила перпендикулярно к плоскости, в которой лежат векторы
Рассмотрим характер движения заряженной частицы в однородном магнитном поле. Пусть заряженная частица с зарядом e движется в однородном магнитном поле со скоростью Это ускорение изменяет лишь направление скорости, величина же ее остается неизменной. Ускорение Подставив сюда выражение для an и решив уравнение относительно R получим: Итак, в случае, когда заряженная частица движется в однородном магнитном поле, перпендикулярном к плоскости, в которой происходит движение, траектория частицы является окружностью. Радиус этой окружности зависит от скорости частицы, магнитной индукции поля и
Попадание заряженной частицы в магнитное поле под произвольным углом a приводит к усложнению ее траектории движения. Траектория движения представляет собой спираль, ось которой совпадает с направлением
ОПИСАНИЕ УСТАНОВКИ Метод определения отношения e/m для электрона, который используется в данной работе, называют «методом магнетрона». Электрическая схема магнетрона изображена на рис.3. Электронная лампа находится внутри соленоида, питаемого током батареи Б1. Сила этого тока измеряется амперметром. Нить катода лампы питается от батареи Б3. Б2 – анодная батарея, создающая постоянную разность потенциалов между сеткой С и катодом К. Сетка соединена с анодом лампы А. Пусть между катодом и сеткой приложена разность потенциалов U. Кинетическая энергия электрона в момент прохождения через сетку равна работе сил электростатического поля, действующих в пространстве между катодом и сеткой: Между анодом и сеткой поле отсутствует. Поэтому от сетки к аноду электроны движутся с постоянной скоростью Замкнем цепь соленоида. При этом внутри соленоида возникнет магнитное поле с индукцией где I – сила тока, проходящего через соленоид; n – число витков на единице длины соленоида; m0=4p·10-7 Гн/м.
Подставив в равенство (7) значения из формул (5) и (6), получим: Таким образом, для вычисления
Поиск по сайту: |
 .
. ,где u – скорость движения частицы; B – индукция магнитного поля.
,где u – скорость движения частицы; B – индукция магнитного поля. , где a - угол между векторами
, где a - угол между векторами  .
. (правило левой руки). В случае отрицательного заряда направления векторов
(правило левой руки). В случае отрицательного заряда направления векторов  и
и  Магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, поэтому она работы над частицей не совершает - действуя на частицу постоянным магнитным полем, нельзя изменить ее энергию.
Магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, поэтому она работы над частицей не совершает - действуя на частицу постоянным магнитным полем, нельзя изменить ее энергию.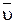 , перпендикулярной к вектору
, перпендикулярной к вектору  . Магнитная сила сообщает заряду нормальное (перпендикулярное к скорости) ускорение
. Магнитная сила сообщает заряду нормальное (перпендикулярное к скорости) ускорение  (1).
(1).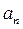 также будет постоянным. При таких условиях частица движется равномерно по окружности, радиус которой можно найти из соотношения:
также будет постоянным. При таких условиях частица движется равномерно по окружности, радиус которой можно найти из соотношения:  (2).
(2). ;
;  (3).
(3). отношения заряда частицы к ее массе. Отношение
отношения заряда частицы к ее массе. Отношение  называется удельным зарядом.
называется удельным зарядом.
 (4).
(4). (5).
(5). (6),
(6), Направление вектора
Направление вектора  , где R – расстояние от сетки до анода, то, согласно 2-го закона Ньютона:
, где R – расстояние от сетки до анода, то, согласно 2-го закона Ньютона:  (7).
(7).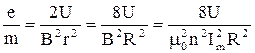 (8).
(8).