 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. ЛАБОРАТОРНАЯ РАБОТА № 1.1Стр 1 из 11Следующая ⇒
ЛАБОРАТОРНАЯ РАБОТА № 1.1 ОПРЕДЕЛЕНИЕ ЦЕНЫ ДЕЛЕНИЯ И ВНУТРЕННЕГО СОПРОТИВЛЕНИЯ ГАЛЬВАНОМЕТРА Цель работы: изучить законы электрического тока и их применение для подключения гальванометра в цепь постоянного тока. Приборы и принадлежности: лабораторная установка.
Основные указания Для выполнения лабораторной работы необходимо знать: закон Ома для участка цепи закон Ома для замкнутой цепи, содержащей источник тока с ЭДС ε , сопротивлением r и два правила Кирхгофа: 1) Алгебраическая сумма токов, сходящихся в узле, равна нулю: 2) Для любого замкнутого контура сумма падений напряжений равна сумме всех ЭДС в этом контуре: ΣIκ Rκ = Σεκ . Применим эти законы и правила к расчету шунта и добавочного сопротивления для гальванометра. Гальванометр-это прибор для измерения очень малых токов и малых напряжений. Электроизмерительные приборы, включенные в цепь последовательно, чтобы не вносить искажений в измеряемые величины, должны иметь минимальное сопротивление, тогда как включенные в цель параллельно – максимальное. При желании, один и тот же гальванометр можно использовать в качестве прибора для измерения большого тока и прибора для измерения большого напряжения. В первом случае к нему нужно параллельно присоединить шунт с малым сопротивлением, во втором - последовательно присоединить большое добавочное сопротивление. Рассчитаем гальванометр - амперметр (рис.1). По первому правилу Кирхгофа
Из равенства (2) следует: Сопоставляя выражения (3) и (4), имеем: Видно, что для увеличения пределов измерения гальванометра по току в Nраз, надо присоединить к нему параллельно шунт с сопротивлением в (N-1) раз меньшим сопротивления гальванометра.
Так как Из уравнения (5) вытекает условие выбора добавочного сопротивления: если нужно измерить напряжение : Отсюда видно, что для увеличения пределов измерения гальванометра по напряжению в Nраз к нему следует последовательно присоединить добавочное сопротивление в (N-1) раз больше сопротивления гальванометра.
Описание установки Отклонение стрелки в приборах магнитоэлектрической системы пропорционально проходящему току: где n - число делений, соответствующее отклонению стрелки; ki - коэффициент пропорциональности, называемый ценой деления по току. Он показывает, какой ток надо пропустить через прибор, чтобы стрелка отклонилась на одно деление. По закону Ома падение напряжения на приборе равно U = Irg (8), где Подставляя выражение (7) в (8), получим: U = kirgn (9). Величина
Согласно закону ома ток на участке АС
Подставляя выражение (11) в формулу (10), получим: откуда Сложив сопротивления R0 ,R1 и rg ,получим: Если взять R0 <<rg , то величиной R0 в знаменателе можно пренебречь по сравнению с R1 +rg. Тогда, при любом изменении R1, RAB = R0. Как следует из уравнения (12), ток в цепи все время будет постоянным: (так как U=const, R=const, R0=const), поэтому падение напряжения на участке АВ UАВ = IR0есть также величина постоянная. Подставляя в это равенство значение силы тока I из формулы (13), получим: С другой стороны: Из формулы (15) видно, что это есть уравнение прямой линии относительно аргумента 1/n. Для двух значений R1,и соответственно n,получим: Решая систему уравнений (16) относительно ki и rg, получим:
Формулы (14), (17), (18), (19) - приближенные и дают хороший результат при условии, что rg>>R.Они являются рабочими. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. 2. Выставить напряжение U по указанию преподавателя или такое, при котором стрелка гальванометра стоит на последнем делении. 3. Определить количество делений n, на которое отклонилась стрелка. 4. Подобрать с помощью магазина сопротивлений такое R1, при котором отклонение стрелки n уменьшается на 4-6 делений и выражается целым числом. 5. Повторить эту процедуру 4-5 раз таким образом, чтобы каждый раз происходило уменьшение n еще на 4-6 делений. Результаты измерений занести в таблицу 1. 6. Построить график зависимости R = f(1/n). Должна получиться прямая линия. 7. Выбрав на графике два значения R1и n,которые наилучшим образом ложатся на прямую (т.е. R1,1 ,n1 и R1,2 ,n2) , вычислить по рабочим формулам ki, rg и kU. 8. Вывести формулы для подсчета относительных погрешностей и произвести их расчет. 9. Результаты измерений и вычислений занести в таблицу 2:
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулируйте закон Ома для участка цепи, для полной цепи и правила Кирхгофа. 2. Назначение гальванометра. 3. Что показывает цена деления электроизмерительного прибора? 4. Как можно увеличить пределы измерения электроизмерительных приборов? 5. Как подключают шунт к гальванометру, чтобы сделать его амперметром? 6. Как подключают добавочное сопротивление к гальванометру, чтобы сделать его вольтметром? 7. Как рассчитать шунт? Как рассчитать добавочное сопротивление? 8. Как определить абсолютную погрешность электроизмерительного прибора?
Поиск по сайту: |
 ;
;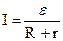 ,
, .
.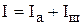 (1), а падение напряжения на участке АВ
(1), а падение напряжения на участке АВ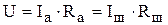 (2), где Rа -спротивление амперметра; Rш - сопртивление шунта.
(2), где Rа -спротивление амперметра; Rш - сопртивление шунта.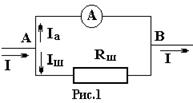 Пусть необходимо увеличить пределы измерения амперметра в Nраз, т.е. сделать возможным измерение тока
Пусть необходимо увеличить пределы измерения амперметра в Nраз, т.е. сделать возможным измерение тока  (3).
(3). , откуда
, откуда 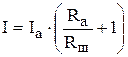 (4).
(4). , откуда
, откуда 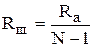 .
.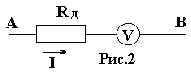 Расчитаем гальванометр - вольтметр (рис.2). По закону Ома UАВ = I(Rд + Rv).
Расчитаем гальванометр - вольтметр (рис.2). По закону Ома UАВ = I(Rд + Rv). , то
, то 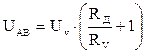 (5).
(5).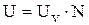 , то необходимо присоединить такое добавочное сопротивление Rд, чтобы
, то необходимо присоединить такое добавочное сопротивление Rд, чтобы 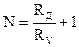 , откуда
, откуда 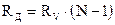 (6).
(6).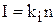 , (7),
, (7),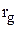 - внутреннее сопротивление гальванометра.
- внутреннее сопротивление гальванометра. называется ценой деления по напряжению.
называется ценой деления по напряжению.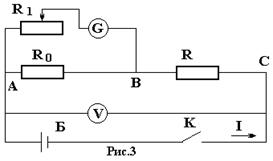 Для определения
Для определения 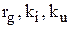 используется схема, приведенная на рис.3. В схеме гальванометр Gработает как амперметр (в этом случае его шунтом является R0)и как вольтметр (в этом случае его добавочным сопротивлением является R). Назначение магазина сопротивлений R1 - изменять ток через гальванометр.
используется схема, приведенная на рис.3. В схеме гальванометр Gработает как амперметр (в этом случае его шунтом является R0)и как вольтметр (в этом случае его добавочным сопротивлением является R). Назначение магазина сопротивлений R1 - изменять ток через гальванометр. (10), где
(10), где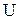 - напряжение на зажимах источника; RAC - сопротивление участка АС: R = RAC + R (11).
- напряжение на зажимах источника; RAC - сопротивление участка АС: R = RAC + R (11).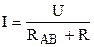 (12),
(12),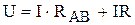 .
.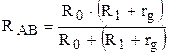 .
.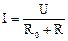 , (13)
, (13)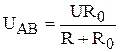 (14).
(14).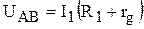 , где
, где 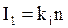 , поэтому
, поэтому 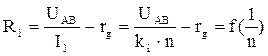 (15).
(15).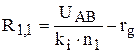 ;
; 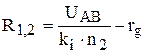 ; (16).
; (16). (17);
(17);  (18);
(18); 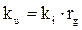 (19).
(19). Установить R1 = 0. Включить установку.
Установить R1 = 0. Включить установку.