 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЗАЛЕЖНІСТЬ УСПІШНОСТІ СТУДЕНТІВ ВІД СТАТІ ⇐ ПредыдущаяСтр 2 из 2
Щільність зв’язку у даному випадку можна розрахувати за допомогою коефіцієнта асоціації:
Тобто між статтю та успішністю студентів зв’язок надто незначний, практично він відсутній. Такий висновок, мабуть, є справедливим, оскільки істотними факторами успішності є не стать, а відвідування лекційних і практичних занять, кількість годин самостійної роботи і т. п. Використання таблиць взаємозалежності дуже поширене при вивченні взаємозв’язку ознак різної природи: в економіці, соціології, біології, медицині. У порівнянні з КРА їх вибір легше аргументувати, легше дотримуватися необхідних умов застосування, а отримані результати інтерпретувати. Ми вже згадували про проблему вибору факторів в КРА, крім того, на практиці не завжди забезпечується виконання відповідних постулатів (взаємозв’язок факторів, нормальність розподілу, відповідність шкал та ін.). Прагнення подолати подібні перешкоди іноді приводить деяких дослідників до віртуозних математичних трюків, аби тільки “притягнути за вуха” наукові методи. Щоб глибоко зрозуміти й оволодіти досягненнями світової статистичної науки, особливо останніх десятиліть, потрібна відповідна підготовка. Ми вважаємо, що спеціалісту з економіки та управління при розв’язуванні прикладних задач за допомогою пакетів статистичних програм перш за все необхідно чітко уявляти, який статистичний інструмент у яких випадках застосовувати, вміти інтерпретувати отримані результати. Саме тому ми настійно рекомендуємо при розв’язуванні конкретної задачі, поки не буде набуто певного досвіду, користуватися прикладами з авторитетних літературних джерел. Це дасть змогу: а) визначити, який метод застосовується в задачі, подібній до Вашої; б) обчисливши контрольний приклад наявними у Вас засобами (статистичними програмами), порівняти значення результатів, їх інтерпретацію та термінологію. У цьому плані із наведеного списку літератури насамперед рекомендуємо [2, 11, 93, 95]. Звичайно, параметричні та непараметричні методи не є взаємозамінюваними. Проте в деяких випадках для зручності замість перших можна застосовувати другі, замінюючи метричні шкали, наприклад, порядковими. Але треба пам’ятати, що менша глибина аналізу, яка буде досягнута при цьому, може бути виправдана лише більшою його аргументованістю та надійністю. Нагадаємо, що за допомогою непараметричних методів можна лише визначити щільність зв’язку та його істотність, КРА дає змогу до того ж вивчити і його форму. Широко відомі міри взаємозв’язку, які не базуються на статистиці c2. Для випадків, коли ТВ побудована для ознак, одна з яких або обидві виміряні за допомогою порядкової шкали, наприклад “колір очей—колір волосся”, найчастіше використовуються так звані методи рангової кореляції: міри Кендалла; Стьюарта та Спiрмена. Якщо ознаки в ТВ тільки дискретні (“стать”, “спеціальність”, але не “вік”), рекомендуються міри Гудмена—Крускала. I нарешті, існує група методів спеціально для ТВ розміром 2 ´ 2 [2, 95]. Популярний приклад: “Палять — не палять; хворіють — не хворіють”. Очевидна умовність такого поділу. Що означає “хворіють”? Як часто? Якими саме захворюваннями? А що означає “не палять”? Зовсім чи не зовсім? Взагалі, однозначні відповіді не завжди коректні. Дійсно, є суто альтернативні ознаки, наприклад “стать” (принаймні, так заведено вважати). Але якщо є змога і дозволяє обсяг сукупності, треба намагатись “розтягнути” шкалу вимірювання. Наприклад, якщо Ви формулюєте питання анкети для соціологічного обстеження персоналу лікарні, то для запитання “Чи задоволені Ви умовамипраці?” слід підказувати такі варіанти відповіді: “Не задоволений”, “Скоріше незадоволений, ніж задоволений”, “Важко відповісти”, “Скоріше задоволений, ніж незадоволений”, “Задоволений”. Якщо Ви запропонуєте тільки два варіанти відповіді і тим самим змусите людину відповісти тільки “задоволений” або “незадоволений”, то Ви не вловите відтінків у настрої людей. Але слід мати на увазі, що іноді корисно зробити і навпаки. Так, згідно з теорією слід уникати застосування ТВ у тих випадках, коли значення окремих клітинок менше 5. Проте є рекомендації, як знайти вихід з цього положення. В літературі та роздруковках статистичних пакетів вони пов’язані з іменами таких авторів, як Й’єйтс (Yates), Кохрен (Сochran), Мантель (Mantel). Але їх застосування потребує певної обережності. У таких випадках іноді краще об’єднати рядки чи стовпчики ТВ. Зрозуміло, що це можна зробити, наприклад, щодо ознаки “задоволеність умовами праці” або “колір волосся”, а не ознаки “спеціальність”. Бажаючим докладніше ознайомитися з методами вивчення взаємозв’язку, пов’язаними з ТВ, ми із задоволенням рекомендуємо [2, 95]. Вважається, що глибокий статистичний аналіз включає не тільки перевірку гіпотези про незалежність, але і порівняння самих критеріїв для більш повного розуміння результатів. Визначення щільності зв’язку за методом кореляційного та дисперсійного аналізу пов’язане з деякими труднощами й потребує громіздких розрахунків. Для орієнтовного оцінювання щільності зв’язку користуються наближеними характеристиками, які не потребують трудомістких розрахунків. До них слід віднести: коефіцієнт кореляції знаків Фехнера, коефіцієнти кореляції рангів Спірмена та Кенделла. Коефіцієнт кореляції знаків Фехнера ґрунтується на зіставленні знаків відхилень від середньої та розрахунку кількості збіжностей і розбіжностей знаків. Він визначається за формулою
де: u — число пар з однаковими знаками відхилень x та y від А от ще один метод оцінювання зв’язку на підставі розрахунку коефіцієнта кореляції рангів. Його головна характерна властивість полягає в тому, що він обчислюється не за первинними даними, а за рангами, які присвоюються всім значенням ознак, що вивчаються, розміщених в порядку зростання. Якщо значення збігаються, то ранг визначається діленням суми рангів на кількість значень. Коефіцієнт кореляції рангів Спірмена визначається за формулою
де: d2 — квадрат різниці рангів для кожної одиниці, d = x – y. Коефіцієнт кореляції рангів Спірмена також коливається в межах від “ –1” до “ +1”. Чим ближче до “1”, тим щільніший зв’язок. Знак “+” чи “–” вказує на напрям зв’язку. Якщо ранги за обома ознаками збігаються, то зв’язок повний, прямий. Якщо r = 0, то зв’язок між ознаками відсутній. Ранговий коефіцієнт кореляції точніший за коефіцієнт кореляції знаків, оскільки він враховує не лише знаки відхилень, а й місце величини ознаки в даному ряді. Крім описаних вище коефіцієнтів на практиці для визначення рейтингу та оцінювання щільності зв’язку використовують коефіцієнт кореляції рангів Кенделла:
де si — сума балів. Сутність цього методу полягає в підрахунку числа балів для кожної одиниці сукупності. Для цього ранг першої одиниці сукупності за ознакою y в упорядкованому за x ряді порівнюємо з рештою одиниць сукупності, розташованою нижче за списком. Якщо він менший, присвоюємо йому бал “+1”, якщо більше — “–1”. 2.5.2. План семінарських занять 1. Поняття “клінічна статистика”, основні завдання її. 2. Поняття “рандомізація”. 3. Принципи порівняння рядів розподілу. 4. Основні особливості застосування статистичних методів при клінічних і лабораторних дослідженнях.
1. Які статистичні методи використовуються в різних видах клінічних і лабораторних досліджень? Наведіть приклади. 2. Що таке рандомізація? Які її засоби Ви знаєте? 3. У чому полягає принцип порівняння рядів розподілу? 4. Що таке статистична гіпотеза? Назвіть приклади її формулювання у випадках клінічних і лабораторних досліджень. 5. На які три групи поділяють критерії статистики? 6. Які статистичні критерії застосовують при порівнянні рядів розподілу за якісною ознакою? за кількісною ознакою? 7. Назвіть умови застосування t-критерію Стьюдента. 8. Назвіть умови застосування критерію χ2 Пірсона. 9. Які критерії називають непараметричними і чому? 10. Що таке “ефект плацебо”? 11. Що вивчає клінічна статистика? 12. Що таке взаємопов’язані вибірки та засоби їх порівняння? 13. Наведіть приклад, коли така характеристика ряду розподілу, як мода, є більш інформативною, ніж середнє значення. Мається на увазі, що рівень ознаки, яка вивчається, вимірюється за допомогою метричної шкали. 14. Як інтерпретується числове значення рівня істотності? 15. Наведіть приклади односторонньої перевірки нульової гіпотези. 16. Як можна порівняти несиметричні розподіли двох сукупностей за кількісною ознакою? 17. Назвіть приклади комбінованого використання методів рандомізації та стратифікації. 18. Які статистичні оцінки називають вінзорізованими? 19. Які статистичні оцінки називають робастниками? 20. Які статистичні сукупності називають однорідними? Що може бути критерієм однорідності? 21. Які Ви знаєте види (модифікації) t-критерію Стьюдента? В яких випадках їх застосовують?
[1] Ефект Готорна (зазвичай позитивний, або корисний) — вплив дослідження на особу, що є його об’єктом. Полягає в тому, що усвідомлення своєї ролі в дослідженні позначається на поведінці особи. Назва походить від назви міста Готорн (штат Іллінойс), на електростанції якого було проведене відповідне дослідження. Від себе додамо, що ефект Готорна є по суті одним з проявлень феномену артефакту.
Поиск по сайту: |
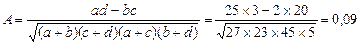 .
.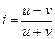 ,
,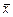 та
та 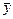 ; v — число пар з різними знаками відхилень x та y від
; v — число пар з різними знаками відхилень x та y від 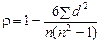 ,
,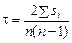 ,
, 2.5.3. Навчальні завдання
2.5.3. Навчальні завдання
