 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Наприклад, для неквадратних таблиць коефіцієнт Чупрова має виглядСтр 1 из 2Следующая ⇒
Методичні поради Клінічна статистика вивчає значущість, достовірність результатів клінічних і лабораторних досліджень. Вони, як правило, пов’язані з оцінкою впливу окремих препаратів на організм, порівнянням окремих методів лікування, визначенням впливу різних факторів на здоров’я людини, оцінкою ефективності певних методів лікування та ін. При цьому широко використовують основні загальновідомі методи статистики: аналізу рядів розподілу, вивчення статистичного зв’язку, перевірки статистичних гіпотез, багатовимірного статистичного аналізу. Більшість цих методів вивчається студентами різних фахових спрямувань: медичного, технічного, економічного. Проте існує певна специфіка їх використання в конкретній предметній області. Це також стосується й інтерпретації отриманих результатів. У цьому розділі навчально-методичного посібника акцент робиться саме на деяких з цих особливостей. Перш за все слід згадати про таку концепцію, як рандомізація, з якою пов’язані методи планування експерименту в умовах неоднорідності, проведення масових спостережень, ретроспективних досліджень та ін. [54]. Статистичні висновки щодо клінічних і лабораторних досліджень багато в чому залежать від того, як провадився відбір об’єктів. Наприклад, порівнюємо дію вітаміну Хв вітчизняного виробництва і вітаміну Хз закордонного виробництва, які мають однакові хімічні формули, на організм людини. Для цього оберемо відповідно дві групи людей А і В і після експерименту порівняємо результати, припустимо, за допомогою всім відомого t-критерію, який показав нам статистично значущу відмінність. Здавалось би, ми маємо, крім імен виробників, одне з яких може бути знаним в усьому світі (як кажуть, brand), ще і статистичні докази переваги одного препарату над так званим аналогом. Це дійсно так, якщо експериментальні одиниці у двох групах ідентичні (наприклад, коли кожна особа з групи А має у групі В якщо не брата-близнюка, то двійника з практично такими самими характеристиками всього організму). Кожен з нас розуміє, наскільки це практично можливо. В соціальних, економічних, біологічних дослідженнях ми маємо справу з неоднорідними, несхожими одиницями. Хоч би як правильно ми підібрали склад порівнюваних груп, достатньої однорідності не досягнемо. Людина, на відміну від електричної лампочки або кульки від шарикопідшипника, характеризується безліччю атрибутів. Проблема полягає в тому, які з них взяти до уваги під час проведення експерименту. На практиці відбір експериментальних одиниць може бути пов’язаний з суб’єктивними, а то й упередженими діями дослідника, що призводить до систематичного зміщення результатів. Рандомізація покликана забезпечити коректність застосування статистичних методів, оскільки є процедурою, що вносить елемент випадковості в експеримент. Рандомізація може проводитися різними засобами. Детальніше з ними можна ознайомитися, звернувшись, зокрема, до публікацій [54, 95]. Коротко викладемо їх суть. Так, наприклад, при перевірці певного лікарського препарату одній групі людей можна давати саме його, іншій — нейтральний (плацебо); можна давати обом групам два різних препарати, але ні лікар, ні пацієнт не знають, який саме з цих двох; можна використовувати таблиці випадкових чисел та ін. Часто методи рандомізації комбінують з методами стратифікації, тобто поділу пацієнтів на певні групи (статеві, вікові, професійні). Після проведення групування в кожній з таких груп провадять рандомізований відбір. Проведення економічного аналізу в галузі охорони здоров’я потребує елементарних знань з епідеміології і, як підкреслюється, особливо з випробувально-інтервеційної складової цієї дисципліни [22, 68]. Тут автори перш за все мають на увазі відомі нам методи порівняння статистичних сукупностей. Наприклад, один з найпростіших — метод “до і після”, за яким вимірюється здоров’я до втручання і після нього. Ми, звичайно, пам’ятаємо про принципи перевірки статистичних гіпотез, про взаємопов’язані та незалежні вибірки та ін. Проте проблема полягає в тому, як при цьому уникнути упередженості або ненавмисних помилок, пов’язаних із впливом на кінцевий результат таких факторів, як природна здатність організму до самозцілення, ефект плацебо, зміни, що сталися за проміжок часу між двома випробуваннями, ефект Готорна[1] тощо. Той, хто вивчав загальну та соціально-економічну статистику за напрямами економічного університету, з цими деталями не обізнаний. Вже сам процес відбору людей в дослідну та контрольну групи може мати в собі деяку упередженість, що в кінці призведе Проте в літературі ми знаходимо застереження, що рандомізація досліджень може видатися неетичною, коли є підстави вважати, що спосіб лікування, який випробується, кращий за альтернативний [22]. І все ж дослідник повинен розуміти, що рандомізовані експерименти мають надійніші результати. В названій роботі згадується про дослідження Кокрейна (Cochrane, 1972), який виявив низку методів лікування, що вважалися дієвими, але при перевірці методом випадкового відбору виявилися неефективними. Це викликало значний резонанс у світі науки (зацікавлені можуть отримати про нього уявлення, детальніше познайомившись з рекомендованою літературою). Особливе місце серед кривих розподілу посідає нормальна крива, яка відображає нормальний розподіл, або розподіл Гауса. Оцінка суттєвості показників асиметрії та ексцесу дає можливість зробити висновок про те, чи можливо віднести даний емпіричний розподіл до типу нормальних кривих вже на попередньому етапі дослідження. Він є результатом впливу необмеженої кількості незалежних один від одного факторів, що в природі зустрічається дуже часто. Поняття нормального розподілу покладено в основу багатьох методів статистики. Особливості кривої нормального розподілу такі: Крива симетрична відносно максимальної ординати. Максимальна ордината відповідає значенню x = Me = Mo, і її величина дорівнює 2. Крива асимптотично наближається до осі абсцис. 3. Крива має дві точки перегину, які знаходяться на відстані ± s від середнього значення. 4. При сталому значенні середньої з ростом s крива стає більш положистою. При зміні середнього значення і сталому значенні s крива не змінює своєї форми і лише зсувається вправо чи вліво по осі абсцис. 5. В інтервалі Нормальний розподіл має місце лише в тому разі, коли на величину ознаки впливає велика кількість випадкових факторів. Вплив цих факторів незалежний, і жоден з них не має переваги над іншими. Наприклад, розподіл великої кількості осіб однієї статі та вікової групи за ознаками “зріст”, “маса” або “артеріальний тиск” буде нормальним у тому разі, коли вони є практично здоровими. Розподіл гіпертоніків за останньою ознакою не буде нормальним. Для перевірки істотності, тобто “невипадковості” відмінності емпіричного розподілу від нормального, застосовують критерії згоди. Одним із найпоширеніших критеріїв згоди є критерій “хі-квадрат”, c2, запропонований К. Пірсоном:
де fi та fi′ — відповідно частоти емпіричного та теоретичного розподілу в зазначеному інтервалі. Чим більшою буде різниця між емпіричними та теоретичними частотами, тим більшою буде величина c2. Для відповіді на запитання про нормальність розподілу фактичне, обчислене нами значення критерію порівнюється із табличним (критичним) значенням при відповідній кількості ступенів вільності і рівні значущості, або істотності (він обирається на рівні 0,05 чи 0,01). Якщо c2ф > c2табл, тобто c2 попадає у критичну область, то це означає, що розбіжність між емпіричними і теоретичними частотами суттєва і її не можна пояснити випадковими коливаннями вибіркових даних. В такому разі нульова гіпотеза про нормальність розподілу відкидається. Якщо c2ф < c2табл, розбіжність між частотами вважається випадковою. Для розрахунку числа ступенів вільності використовується різниця між кількістю груп (k) та кількістю обмежень (l). Для перевірки гіпотези про нормальність l = 3. При розрахунку критерію Пірсона необхідною є відповідність декільком умовам: 1) чисельність спостережень повинна бути не меншою за 50; 2) частоти у кожному інтервалі — не меншими від 5. Існує ще один критерій перевірки відповідності нормальному розподілу — це критерій Колмогорова—Смирнова. Він заснований на розрахунку максимальної різниці (d) між відносними частотами в емпіричному і теоретичному розподілах за абсолютною величиною, находженні числа Якщо dф > Якщо dф < У процесі статистичного аналізу часто виникає необхідність порівняння рядів розподілу. Якщо ми маємо емпіричний ряд розподілу і підбираємо теоретичну криву, яка б найповніше відображала закономірність розподілу, то цей процес називається моделюванням. При цьому виникає питання, якою мірою вибрана нами теоретична крива узгоджується з емпіричною, подібна до неї. В іншому випадку необхідно порівняти дві емпіричні криві. Тут йдеться про те, наскільки вони схожі або, точніше, чи суттєво вони різняться. Інакше кажучи, чи суттєво різняться ті сукупності, розподіли яких відображені цими кривими. У практиці статистичних досліджень в галузях економіки, соціології, біології та ін. така необхідність зустрічається дуже часто (приклади 2.5.1—2.5.5). Приклад 2.5.1. Маємо дані про масу тварин у контрольній та дослідній групах, останні отримували певну кормову добавку:
Чи сприяє запропонована кормова добавка збільшенню маси тварин? Приклад 2.5.2. Маємо дані про місячні заробітки працівників, що виконують однакову роботу, на двох малих підприємствах, грн.:
Чи однаково заробляють працівники цих підприємств? Приклад 2.5.3. При анкетуванні працівників підприємства на запитання “Чи задоволені Ви умовами праці?” відповіді чоловіків і жінок розділилися так:
Чи однакове ставлення чоловіків і жінок до умов праці на їхньому підприємстві? (c2 = 1,04). Приклад 2.5.4. Маємо дані про врожайність культури на дослідній та контрольній ділянках за ряд років, ц/га:
Чи впливає попередній обробіток посівного матеріалу на врожайність культури? (t = 7,32). Приклад 2.5.5. При визначенні pH розчину в 10 пробах було отримано значення 7,48 ± 0,21. Чи можна вважати реакцію даного розчину лужною, якщо такими вважаються реакції зі значеннями pH > 7,0? (t = 2,28). Прикладів можна навести безліч, але мовою статистики суть питання формулюється так: чи є дві задані сукупності (тобто ті, що порівнюються) вибірками із тієї самої генеральної сукупності або з двох різних генеральних сукупностей? Практично завжди між двома сукупностями, точніше розподілами їх за певною ознакою, існує певна відмінність. Наприклад, розподіл за ознакою “зріст” студентів, які в даний момент знаходяться на п’ятому поверсі університету, буде відрізнятися від розподілу тих, хто перебуває на другому поверсі, але питання в тому, випадкова ця відмінність чи ні, тобто достовірна, суттєва, істотна. Таким чином перевіряється гіпотеза про відсутність реальної відмінності, яку називаютьнульовою гіпотезою і позначають Н0. Для її перевірки використовують різні методи (оцінки) — статистичні критерії. Рівень істотності характеризує, якою мірою дослідник ризикує зробити помилку, відхиляючи Н0. Важливо пам’ятати про такі обставини: 1. Слова “істотна”, яким ми характеризуємо відмінність між рядами розподілу, характеризує не її величину, а її “невипадковість”. 2. Відсутність достатніх підстав для відхилення Н0 не є доказом відсутності відмінності. 3. Залежно від обставин один і той самий критерій слід обчислювати за різними формулами. 4. Рівень істотності повинен обирати сам дослідник, беручи Очевидно, що роль критерію в статистичному дослідженні, можливі наслідки прийнятих рішень вимагають коректного його застосування. Принципове значення при виборі критерію в кожному конкретному випадку має характер сукупностей, що порівнюються, — вид ознаки, форма розподілу, обсяги вибірок та ін. Беручи до уваги важливу роль цих методів в статистичному аналізі та багато пов’язаних з ними нюансів, рекомендуємо в практичній роботі користуватися відповідною літературою [2, 11, 90, 93, 95]. Деякі критерії можуть бути використані у випадках розподілів, близьких до нормального. При цьому відмінність між розподілами може оцінюватися шляхом порівняння їх середніх. Для цього може бути використано t-критерій Стьюдента (приклад 2.5.1, [93]). Приклад 2.5.2 має нагадувати, до якого абсурду можна дійти, оперуючи середніми рівнями (заробітку, радіації, кількості шуб на одну жіночу душу), помилково чи свідомо не звертаючи при цьому увагу на форму розподілу. При абсолютно однакових “середніх” насправді маємо абсолютно протилежні принципи оплати праці. Коли ж порівнюються розподіли якісної ознаки (приклад 2.5.3), то може бути використано критерій “хі-квадрат” Пірсона. При цьому необхідно, щоб обсяги порівнюваних вибірок були не менше 20—30 одиниць, а частоти в окремих клітинках не менше 4—5 [93]. Існують критерії, застосування яких не потребує обчислення параметрів розподілу (середнього, дисперсії та ін.) і які отримали назву непараметричних. Їх можна розділити на три групи [93, 96]: · критерії, що виявляють відмінність характеристик центру; · критерії, що дають змогу виявити будь-яку відмінність, але не дають відповідь, у чому саме вона полягає; · критерії для попарно узгоджених сукупностей. В. Ю. Урбах наводить по два приклади обчислення критеріїв, що представляють кожну групу, та відповідні пояснення [93]. Це відповідно: критерій Уайта і критерій Х (Ван дер Вардена); серійний критерій та критерій Колмогорова—Смирнова; критерій знаків і критерій Вілкоксона. t-критерій Стьюдента використовують для перевірки гіпотези про середні двох нормально розподілених генеральних сукупностей. Частою помилкою є ігнорування припущень про дисперсії розподілів. Якщо ж взяти до уваги дані про ці параметри, то формули для обчислення t-критерію будуть різними. При цьому, як відомо, виділяють 4 випадки [75]. Зупинимося на випадках незалежних і залежних (взаємопов’язаних) вибірок. Випадок незалежних вибірок маємо в прикладі 2.5.1. Критерій обчислено за формулою
де:
Число ступенів вільності f = n1 + n2 – 2 = 32 + 23 – 2 = 53. Величина, що стоїть в знаменнику формули (2.5.1) і має назву середньої помилки різниці, обчислюється як mрізн = У таких випадках сукупності називають залежними, або попарно зв’язаними, і тоді [93]: mрізн =
де: хі, уі — попарно зв’язані варіанти. Цей випадок ілюструє приклад 2.5.4. Число ступенів вільності при цьому: f = n – 1 = 7 – 1 = 6. Розглядаючи різні методи вивчення статистичного зв’язку, важливо зрозуміти специфіку, умови їх застосування. В кореляційно-регресійному аналізі (КРА) факторні та результативні ознаки належать до метричної шкали; метод аналітичного групування та дисперсійний аналіз можуть бути реалізовані, коли факторна ознака якісна. Нарешті, у випадку, коли і факторна і результативна ознаки якісні, тобто віднесені до номінальної або порядкової шкали, використовуються так звані непараметричні методи, тобто такі, які не потребують обчислення параметрів розподілу. В чому полягає їх принцип? Для порівняння рядів розподілу якісної ознаки може бути застосований критерій. Але тут ми переходимо до гіпотези про незалежність. Критерій може бути використаний для доказу наявності істотного зв’язку. Коли ознаки якісні, вести мову про форму зв’язку, мабуть, немає сенсу, що ж до напряму, то його іноді можна визначити візуально по самій таблиці взаємозалежності (ТВ). Для визначення щільності зв’язку використовують коефіцієнти взаємозалежності. Наприклад, для неквадратних таблиць коефіцієнт Чупрова має вигляд
де: k1, k2 — кількість рядків і стовпчиків таблиці; n — число елементів сукупності.
Поиск по сайту: |
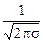 .
. ± s (t = 1) знаходиться 68,3% усіх значень. В інтервалі
± s (t = 1) знаходиться 68,3% усіх значень. В інтервалі  ,
,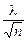 та порівнянні його із розрахунковим при заданому рівні істотності K(l) = 0,09505.
та порівнянні його із розрахунковим при заданому рівні істотності K(l) = 0,09505.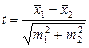 , (2.5.1)
, (2.5.1)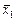 — середнє значення;
— середнє значення; ,
, 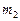 — стандартна помилка середнього (standard error of mean);
— стандартна помилка середнього (standard error of mean);  , де n — обсяг сукупності.
, де n — обсяг сукупності. тільки в тому разі, коли варіанти однієї сукупності не залежать від варіантів другої. Але часто, особливо в практиці біологічних дослідів, буває інакше. Наприклад, при вивченні врожайності на двох розміщених поруч ділянках, рівня холестерину в певній групі осіб до і після лікування і т. д. Можна сказати, що в першому випадку зв’язок реалізується через однакові кліматичні умови, в другому — через один і той же організм.
тільки в тому разі, коли варіанти однієї сукупності не залежать від варіантів другої. Але часто, особливо в практиці біологічних дослідів, буває інакше. Наприклад, при вивченні врожайності на двох розміщених поруч ділянках, рівня холестерину в певній групі осіб до і після лікування і т. д. Можна сказати, що в першому випадку зв’язок реалізується через однакові кліматичні умови, в другому — через один і той же організм. ; (2.5.2)
; (2.5.2) ;
;  ,
,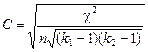 ,
,