|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методические указания к лабораторной работе №6 «Расчёт режима охлаждения изолированной жилы» ⇐ ПредыдущаяСтр 6 из 6
Цель лабораторной работы - изучение процесса охлаждения изолированной жилы. Задачей лабораторной работы является исследование влияния параметров технологического режима охлаждения изолированной жилы на процесс охлаждения с применением метода математического моделирования и численных методов. Цель данной лабораторной работы заключается в определении температурного поля в сечениях проводника и изоляции с целью выбора рационального режима охлаждения т. е. правильного выбора скорости изолирования V0, длины охлаждающей ванны и температуры воды в секциях охлаждающей ванны. Для определения температурного поля в сечении проводника и изоляции существуют несколько моделей, рассмотрим некоторые из них.
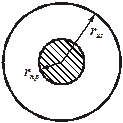
Модель №1 Геометрия изолированной жилы представлена на рис.1.
Рис.1. Геометрия изолированной жилы
Допущения данной модели: – процесс стационарный; – теплофизические параметры постоянны; – диффузией тепла в направлении оси z можно пренебречь; – температура жилы не изменяется. Уравнение энергии будет иметь вид:
Граничные условия:
где Тпр – температура жилы провода; Тср – температура среды (воды) в охлаждающей ванне. Начальные условия:
где Твых – температура изоляции на выходе из кабельной головки. Для решения данной задачи воспользуемся методом конечных разностей. Выберем равномерную сетку по z и r:
Аппроксимируем производные и получим:
С учётом выражений (2) выражение (1), граничные и начальные условия будут иметь вид:
Преобразуем выражения (3):
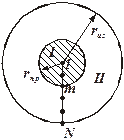
Алгоритм решения данной задачи: – с учётом начальных условий рассчитываем температуру Тi,1; – по выражению (4) рассчитываем поле температур для шага по длине j+1; – по выражению (5) рассчитываем температуры в точка на границе изоляции; – переходим к следующему шагу по длине z и повторяем расчёт сначала. Модель №2 Данная модель охлаждения изолированной жилы отличается от предыдущей тем, что температура провода изменяется по длине охлаждающей ванны, а все остальные допущения остаются в силе. Схема разбиения области конечным числом узлов представлена на рис.2. Уравнения энергии для изоляции и для жилы соответственно будут иметь вид:
Рис.2. Схема разбиения
Граничные условия:
Начальные условия:
Также как и в предыдущем случае для решения системы дифференциальных уравнений (4) используем метод конечных разностей. Разностные уравнения (использована явная разностная схема)имеют вид:
Алгоритм решения данной задачи: – с учётом начальных условий рассчитываем температурное поле по выражениям (7) и (8) во внутренних точках областей I и II; – по выражениям (9), рассчитывается температура в граничных точках; – переходим к следующему шагу по длине z и повторяем расчёт сначала. В случае решения данной задачи по неявной разностной схеме для каждой из областей на каждом шаге по длине решается система алгебраических уравнений, пересчитываются значения температур на границах и переходят к следующему шагу по длине. Модель №3 Данная модель охлаждения изолированной жилы отличается от предыдущей тем, что отбрасывается допущение о постоянстве теплофизических характеристик материала, а все остальные допущения остаются в силе.
Рис.3. Зависимость теплофизических характеристик от температуры
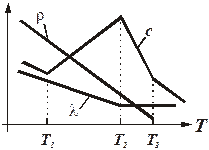
Теплофизические характеристики для текущей точки можно определить (ниже приведён пример для теплоемкости с):
При решении задачи методом конечных разностей можно воспользоваться постановкой задачи для модели 2. Алгоритм решения данной задачи: – с учётом начальных условий рассчитываем температуру Тi,1; – по выражениям (5) и (6) рассчитываем температурное поле во внутренних точках областей I и II; – по выражениям (7), (8) и (9) рассчитывается температура в точках на границе изоляции и между изоляцией и жилой а также в точке, лежащей в центре жилы; – пересчитываем значения теплофизических характеристик для каждой точки сечения; – пересчитываем поле температур в соответствии с выражениями (5), (6), (7), (8) и (9) для этого же сечения и пересчитываем теплофизических характеристики, повторяем расчёт до тех пор пока разность между предыдущими значениями и значениями полученными в текущем расчёте не будет меньше некоторой величины, взятой за погрешность; – переходим к следующему шагу по длине z и повторяем расчёт сначала. Задание В соответствии со своим вариантом задания выполнить следующие расчеты. 1) Для заданного номинального технологического режима и заданных теплофизических характеристик материалов: – разработать алгоритм и расчетную программу; – рассчитать температурное поле в сечении изолированной жилы на выходе из каждой секции охлаждения; 2) Исследовать влияние на распределение температуры по сечению изолировыанной жилы следующих факторов: – теплофизических характеристик материалов; – линейной скорости изолирования жилы; – температур по секциям охлаждения; – толщины изоляции жилы; 3) Провести анализ полученных закономерностей. 4) Построить графики полученных зависимостей. 5) Оформить отчет.
Варианты заданий Для всех вариантов заданий:
Lвоз = 0.6м,
Технологические и теплофизические характеристки
6.3 Контрольные вопросы Какие допущения принимаются при расчёте температурного поля в сечении изолированной жилы для каждой модели? В чем отличия моделей расчёта температурного поля? Сформулировать основные положения метода конечных разностей. Какие виды сеток существуют? В чём суть аппроксимации производных?
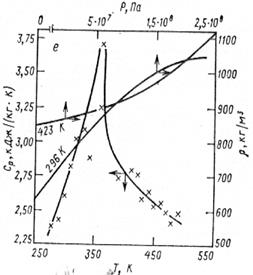
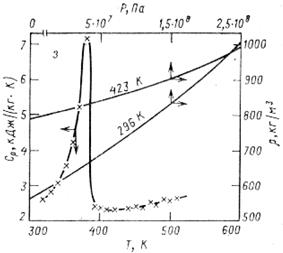
ПРИЛОЖЕНИЕ Теплофизические характеристики полимерных материалов приведены на рис.1.
а б Рис. 1. Зависимость теплоёмкости и плотности полимеров от температуры и давления: а – полиэтилен высокой плотности; б – полиэтилен низкой плотности алатон ТМ 1540.
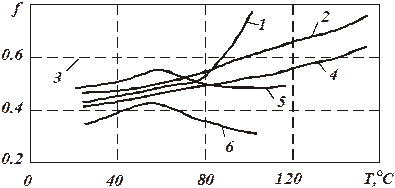
Реологические характеристики полимерных материалов приведены на рис.2.
Рис. 2. Зависимость коэффициента трения от температуры для полимеров: 1 – ПВХ; 2 – полиамид 6.6 (сорт А); 3 – полиамид 6.6; 4-полиамид 6.6 (сорт В); 5 – полипропилен; 6 – полиэтилен.
Поиск по сайту: |
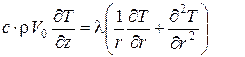 (1)
(1)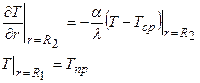


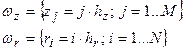
 (2)
(2)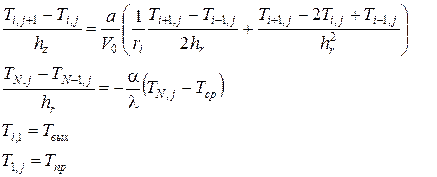 (3)
(3)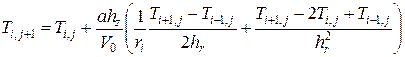 , (4)
, (4) . (5)
. (5) (6)
(6)


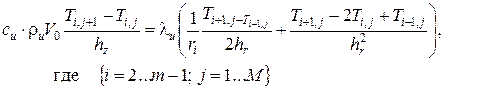 (7)
(7)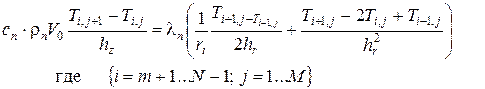 (8)
(8)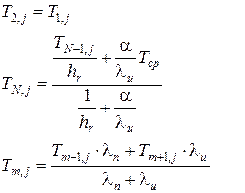 (9)
(9)
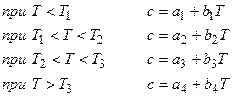
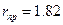 мм,
мм, 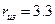 мм,
мм,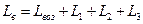
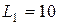 м,
м, 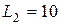 м,
м,  м
м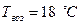
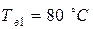
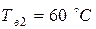
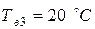
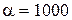 Дж/(м2 ∙с∙ ○ С)
Дж/(м2 ∙с∙ ○ С) 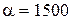 Дж/(м2 ∙с∙ ○ С)
Дж/(м2 ∙с∙ ○ С) 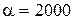 Дж/(м2 ∙с∙ ○ С)
Дж/(м2 ∙с∙ ○ С)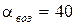 Дж/(м2 ∙с∙ ○ С)
Дж/(м2 ∙с∙ ○ С)