|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методические указания к лабораторной работе №3 «Расчёт зоны плавления»
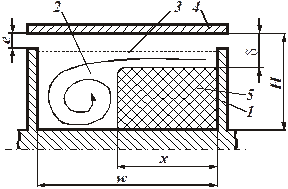
Цель лабораторной работы - изучение процессов тепломассопереноса полимера в зоне плавления червячного пресса. Задачей лабораторной работы является исследование влияния геометрических, технологических и физических факторов на изучаемый процесс с использованием метода математического моделирования Краткие теоретические сведения Экструзия - это технологический процесс, сущность которого состоит в придании материалу нужной формы путем продавливания материала через профилирующий инструмент (матрицу). Процесс экструзии включает в себя четыре элементарных стадии, разделенные по зонам: загрузки, задержки плавления, плавления и дозирования. В зоне плавления материал переходит из твердого состояния в жидкое под воздействием тепла, подводимого от стенок корпуса, и тепла, выделяющегося в результате вязкого трения. Многочисленные исследования показывают, что процессы, происходящие в зоне плавления, для всех пластифицирующих экструдеров примерно одинаковы. Полимер в твердом состоянии, называемый пробкой гранул, двигается по винтовому каналу червяка и попадает в участок корпуса, где температура внутренней поверхности корпуса выше температуры плавления материала. Контактирующая со стенкой поверхность полимера начинает плавиться, и на внутренней поверхности корпуса экструдера образуется тонкая пленка расплава. В тот момент, когда толщина этой пленки d (см.рис.6) оказывается больше, чем величина радиального зазора e между гребнем нарезки червяка и стенкой корпуса, толкающая стенка канала червяка начинает соскребать слой расплава с внутренней стенки корпуса и собирать его в области, непосредственно примыкающей к передней грани толкающей стенки. По мере движения пробки ширина области, заполненной расплавом (W‑X), постепенно увеличивается, а ширина твердой пробки X, соответственно, уменьшается. Этот механизм плавления представлен на рис. 1. Процесс плавления заканчивается в тот момент, когда пробка исчезает.
Рис.1. Схематическое представление механизма плавления полимера: 1 - червяк ; 2 - бассейн расплава ; 3- пленка расплава; 4 - корпус экструдера; 5 - твердая пробка полимера; е - зазор между гребнем червяка и корпусом экструдера; d - толщина слоя расплава; w - ширина канала; H - высота канала; x- ширина твердой фазы. Очевидным следствием такого механизма плавления является зависимость длины зоны плавления от основных параметров технологического режима: производительности и заданного распределения температур. Естественно, что интенсивность процесса плавления должна быть достаточно высока для того, чтобы процесс плавления успел закончиться и канал червяка оказался заполненным расплавом прежде, чем материал подойдет к формующей головке. Поэтому основным назначением математической модели процесса плавления в экструдере является предсказание количества переплавленного полимера в любом сечении канала экструдера; длины экструдера, необходимой для полного плавления полимера и зависимость этой величины от геометрии экструдера, условий переработки и свойств материала. Для описания процессов тепломассопереноса в зоне плавления будем использовать принцип обращенного движения. Кроме того, т. к. высота канала много меньше, чем внутренний диаметр шнека, то кривизной канала можно пренебречь. В этом случае, развернув канал, как ленту серпантина, можно рассматривать процесс в длинном прямоугольном канале, дно которого и боковые стенки, образованные поверхностью спиральной нарезки червяка, неподвижны, а верхняя стенка, образованная внутренней поверхностью корпуса, движется с постоянной скоростью Vk, равной окружной скорости вращения червяка и направленной под углом j к продольной оси канала z. Этот угол соответствует углу подъема винтовой линии шнека (рис. 2).
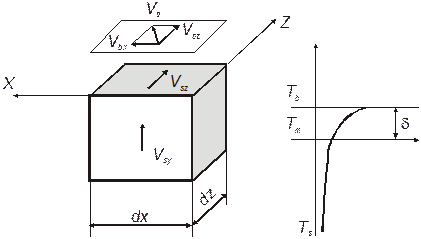
Рис.2. Геометрическая модель канала. Для математического описания процессов движения и плавления в канале пластицирующего экструдера возможно использовать различные подходы, основанные на тех или иных упрощающих предположениях. Наиболее простой математической моделью процесса плавления является модель З.Тадмора, позволяющая в одномерной постановке определить зависимость длины зоны плавления от различных технологических, геометрических характеристик и свойств перерабатываемого материала. Допущения модели Тадмора: 1) кривизной канала пренебрегаем; 2) процесс стационарный; 3) расплав является ньютоновской жидкостью; 4) в целом задача одномерная; 5) характеристики материала постоянны; 6) пробка гранул имеет прямоугольную форму; 7) плавление происходит только у внутренней поверхности корпуса; 8) температура пробки гранул изменяется только по высоте канала; Представление процессов движения и теплообмена полимеров основывается на законах сохранения массы, количества движения и энергии. Главной задачей исследования является нахождение длины зоны плавления, которая определяется длиной канала, где ширина твердой фазы обращается в нуль. Обозначим ширину пробки гранул через X, получим зависимость X=X(z), т. е. изменение ширины пробки по длине канала. Выделим из пробки гранул элементарный объем. На рис. 3 представлен элементарный фрагмент пробки и распределение температуры в поперечном сечении канала
Рис. 3. Элементарный объём пробки гранул и температурный профиль пробки гранул
Где Vb – окружная скорость; Vbz – компонента окружной скорости в направлении оси z; Vbx – компонента окружной скорости в направлении оси x; Vsz – скорость пробки вдоль оси z; Vsy – скорость пробки вдоль оси y; Tb – температура корпуса; Ts – температура загружаемого материала, n – частота вращения шнека. Пробка гранул движется с локальной скоростью Vsz, направленной вдоль канала червяка. Скорость твердой пробки относительно поверхности (относительная скорость Vj) цилиндра находится как:
Введение относительной скорости Vj позволяет упростить задачу (в частности, это касается граничных условий). Гидродинамика расплава, с учетом указанных ранее допущений, описывается следующими уравнениями движения и граничными условиями:
Интегрируя уравнение (4) с учетом (5), получим изменение скорости расплава в пленке в зависимости от координаты y по высоте:
Рассмотрим уравнение энергии для жидкой фазы в пленке толщиной d:
Граничные условия:
Отметим, что все теплофизические характеристики для расплава будем обозначать индексом m (от слова melt – расплав) , а для твердой фазы – s (stone – камень). Проинтегрируем (7) с учетом (6) и (8):
Уравнения (6) и (9) описывают процессы тепломассообмена в пленке расплава. Для твердой фазы уравнения энергии имеют следующий вид:
Решение уравнения (10) с учетом (11) позволяет определить изменение температуры пробки по высоте:
где Отсюда видно, что распределение температуры в пробке не зависит от координаты z, следовательно, не изменяется по длине, сохраняя один и тот же вид зависимости. Используя уравнения (12) и (9), определим величины потоков тепла на границе раздела твердой и жидкой фаз.
где l – теплота фазового перехода, Дж/кг. Уравнение (13) связывает толщину слоя расплава d со скоростью Vsy. Для определения последних составим уравнение баланса масс в жидкой фазе. Пренебрегая малыми величинами, будем иметь:
где w – скорость плавления материала на единичной длине канала, кг/м/с. Откуда:
Подставляя уравнение (14) в уравнение (13) и выражая величину d, получим:
Для скорости плавления имеем выражение:
Приближаясь к решению задачи, т. е. к определению зависимости X=X(z), запишем уравнение баланса фаз, теперь для твердой фазы на участке dz и, переходя к пределу, получим уравнение:
Где выражение для w(X), полученное на основании вышеизложенных выкладок, определяется уравнением (16). Проинтегрируем уравнение (17) с учетом условия X(0)=w, для канала постоянной глубины будем иметь:
Из выражения (18), положив X=0, определяем длину зоны плавления:
Для канала переменной глубины, высота которого изменяется по закону : H=Hl-A×z , где H(0)=Hl, A- угол конусности червяка, решение выглядит так:
Длина зоны плавления в этом случае определится:
Теплофизические и реологические характеристики некоторых полимеров смотри в приложении. Задание В соответствии со своим вариантом задания выполнить следующие расчеты. 1) Для заданного номинального технологического режима: – разработать алгоритм и расчетную программу; – рассчитать компоненты скоростей и относительную скорость; – определить длину зоны плавления, определить Ф и Y; определить длину зоны плавления для канала постоянной глубины, для канала переменной глубины; – рассчитать ширину твердой пробки в зависимости от длины зоны плавления или для канала постоянной или переменной глубины соответственно; – определить распределение скорости плавления по длине; – рассчитать распределение температуры по высоте канала в пяти различных сечениях в зоне плавления для жидкой и твердой фаз соответственно. 2) Исследовать влияние на процесс плавления полимера следующих факторов: – температуры корпуса; – начальной температуры материала; – частоты вращения шнека; – расхода материала; – физико-механических свойств материала; – угла конусности винтовой нарезки червяка. 3) Провести анализ полученных закономерностей процессов тепломассопереноса полимера в зоне плавления экструдера. 4) Построить графики полученных зависимостей. 5) Оформить отчет.
Исходные данные
Свойства материалов
λ=130000 Дж/кг
Геометрические и технологические характеристики экструдеров
На рис.4-рис.6 приведены характерные зависимости теплофизических характеристик полимеров от температуры.
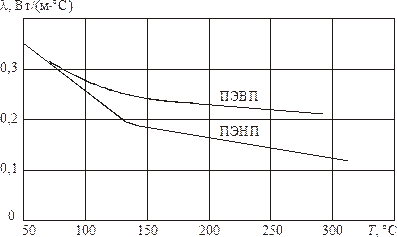
Рис. 4. Зависимость теплопроводности полимеров от температуры
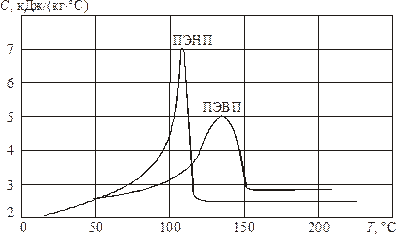
Рис. 5. Зависимость удельной теплоемкости полимеров от температуры
Рис. 6. Зависимость плотности полимеров от температуры
3.3 Контрольные вопросы Что такое экструзия? Какие допущения для расчета по модели Тадмора принимаются? Для чего вводят скорость Vj и каков ее смысл? Каков механизм плавления полимера в червячном прессе? В чем суть принципа обращенного движения?
Поиск по сайту: |

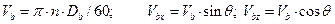 (1)
(1)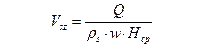 (2)
(2)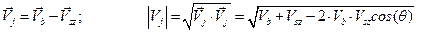 (3)
(3) (4)
(4) (5)
(5)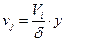 (6)
(6)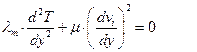 (7)
(7)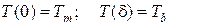 (8)
(8) (9)
(9)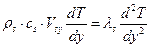 , (10)
, (10) . (11)
. (11)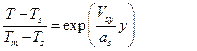 (12)
(12)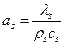
 (13)
(13)
 (14)
(14)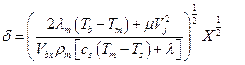 (15)
(15)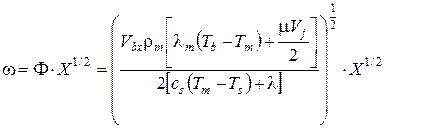 (16)
(16)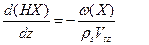 (17)
(17)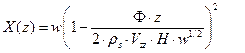 (18)
(18)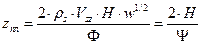 (19)
(19)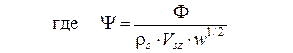
 (20)
(20) (21)
(21)