 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связь параметров газа с его микроструктурой. Распределение Максвелла
Процесс — это переход системы из одного состояния в другое через некоторую последовательность промежуточных состояний. Важной схематизацией, часто используемой в молекулярной физике, является понятие о равновесном процессе. Равновесным называют состояние, если характеризующие его параметры при отсутствии внешних воздействий постоянны неограниченное время, иначе — состояние неравновесное. Равновесное состояние изображается точкой в координатной плоскости, если по осям отложить значения каких-либо двух параметров системы. Неравновесное состояние так изобразить нельзя, так как параметры имеют неопределенные значения. Процесс перехода системы из одного равновесного состояния в другое всегда связан с нарушением равновесия системы. Но если это происходит медленно, то за любой малый промежуток времени состояние системы можно охарактеризовать определенными значениями параметров. И такой процесс можно считать состоящим из ряда равновесных процессов. Равновесный процесс состоит из непрерывной последовательности равновесных состояний, и чем медленнее протекает процесс, тем он больше похож на равновесный. Только равновесный процесс можно изобразить непрерывной линией на графике.
Рассматривая газ как совокупность мельчайших упругих шариков — атомов, которые хаотично двигаются в пустоте, А.Крениг из вероятностных соображений принял, что атомы газа движутся по трем взаимно перпендикулярным направлениям с одинаковой скоростью. Элементарный расчет дал уравнение, связывающее давление р и объем V газа с его массой т и скоростью атомов ниг в 1856 г. верно указал на связь pV с кинетической энергией частиц, получил из кинетической модели закон Авогадро и объяснил охлаждение газа при адиабатическом (хотя при оценке давления он взял коэффициент 1/6 вместо 1/3). Работа Кренига подтолкнула Клаузиуса к опубликованию своих результатов (1857). Рассматривая удар молекул о стенку по законам упругих столкновений, Клаузиус вывел:
где К — энергия поступательного движения всех частиц газа. Поскольку давление и объем идеального газа связаны уравнением Клапейрона, он получил: Больцмана. Кинетическая теория объяснила многие явления — теплопроводность, диффузию, растворение и др., позволила рассчитать сначала относительные и абсолютные значения средних скоростей молекул разных газов, найти средний свободный пробег молекулы — среднее значение длины прямолинейного пути, проходимого молекулой между последовательными соударениями. Его дал Дж. Максвелл в 1866 г. Отсюда нетрудно посчитать и с р е д н е е число соударен и й частицы за определенное время. При обычных условиях оно велико — около 5 млрд соударений за 1 с. Подведение теплоты увеличивает кинетическую энергию движения частиц, растут давление и температура. Как только они достигают высоких значений, возрастает вероятность столкновений между частицами, и сходство газов исчезает. Поступающая в газ энергия должна как-то распределиться между атомами. Но одна часть атомов движется быстрее, другая — медленнее, а их средняя кинетическая энергия пропорциональна температуре газа Т. Если к сосудам, содержащим равное число молекул двух разных газов, подвести равное количество теплоты, то их температура повысится на одну и ту же величину, т.е. удельные теплоемкости с, приходящиеся на одну молекулу, одинаковы. Распределение молекул по скоростям определяет распределение энергий, или энергетический спектр газа, от которого зависят многие свойства газов. В состоянии равновесия все направления скоростей равновероятны, иначе тепловое движение частиц не было бы беспорядочным, но равными по величине они быть не могут. Если такое и случится, то столкновения быстро изменят эту ситуацию. Максвелл рассуждал следующим образом: ни одно направление движения и ни одно значение скорости не являются выделенным, и предоставленный самому себе газ приходит в стационарное состояние с определенным распределением скоростей (рис. 4.5). Поскольку по всем трем осям проекции скоростей должны быть независимы и равновероятны, можно записать причем все вероятности распределения вый вид. Кроме того, с одинаковой вероятностью будут встречаться скорости вдоль каждой оси и против нее, т. е. вероятность должна зависеть от квадрата скоростей
Таким образом, нужно найти функцию от суммы величин, которая распадается на произведение таких же функций от каждого слагаемого в отдельности. Этим свойством обладает только показательная функция. Например, для основания степени числа Среднее значение кинетической энергии имеет размерность квадрата скорости:
Можно показать, что никакая другая функция распределения, кроме рестности нуля, т.е. в газе больше всего молекул с нулевыми значениями компонент скорости. Это связано с равной вероятностью направлений скоростей, так что средняя проекция скорости хаотического движения на любое направление равна нулю. Гауссовы распределения встречаются в разных системах (даже в социальных). Площадь под кривой соответствует общему числу молекул газа. Максвелл рассматривал свою модель газа как математическую аналогию реальности. «Вместо того, чтобы говорить, что все частицы тверды, упруги и шарообразны, можно сказать, что частицы являются центрами сил, действие которых ощутимо лишь на некотором малом расстоянии, где они проявляются внезапно и в виде очень интенсивной силы отталкивания». Далее он проводит сопоставление с величинами, характеризующими тепловое движение, заменяя среднюю скорость распределением скоростей (1859). Проведя ряд опытов, Максвелл заключил, что сила отталкивания должна быть обратно пропорциональна пятой степени расстояния между молекулами. В 1866 г. он вывел свой закон распределения по скоростям уже с этой поправкой. Распределением Максвелла называется распределение молекул по проекции скорости, определяемое функцией
Абсолютное значение скорости не может быть отрицательным, и функция распределения по абсолютному значению скорости начинается с ее нулевого значения:
Основное отличие от предыдущего распределения заключается в существовании множителя — квадрата скорости. Поскольку возрастает квадрат скорости, получающееся распределение асимметрично. Максимум функции F(v) имеет место при наиболее вероятной скорости
Распределению Максвелла удовлетворяют закон сохранения энергии и принцип детального равновесия в отдельных соударениях, когда при хаотическом движении в газе скомпенсированы два противоположно направленных процесса с равными скоростями. Этот принцип справедлив не только для газов, но и для любых систем в состоянии полного хаоса. 4.9. Распределение частиц газа во внешнем поле и в атмосферах планет Распределение Больцмана— это распределение газа по занимаемому объему, если газ находится во внешнем поле; оно отлично от равномерного. Для газа в поле силы тяготения имеет место барометрическая формула Формулу В соответствии с этой формулой, концентрация тяжелого газа в атмосфере должна убывать быстрее, чем легкого, и слой атмосферы на высоте более 60 км должен состоять уже из самых легких газов — водорода и гелия. Но из-за сильного перемешивания атмосфера однородна по составу на высоте до 90 км, меняясь лишь с высоты 95 км. Причина отклонения — диссоциация молекул под действием жесткого ультрафиолетового излучения Солнца. Считалось, что потенциальная энергия равна mgh, что верно для При удалении от Земли на бесконечно большое расстояние п(r) сохраняет конечное значение, что, странно. Земная атмосфера не может простираться до бесконечности, а этот множитель показывает, во сколько раз плотность атмосферы на бесконечности должна быть меньше, чем на поверхности Земли. Парадокс в том, что, если наступит статистическое равновесие, улетучится атмосфера Земли. Но множитель мал, и такого не случится. Для оценки величины показателя степени умножим и разделим его на число Авогадро N. В знаменателе заменим N = RT, в числителе учтем, что Nmравно молекулярному весу. Подставляя значения Для Луны это число порядка 10-25 и тоже мало, но не так, как для данных Земли. Если бы атмосфера у поверхности Луны была такой же, как у поверхности Земли, т.е. равна 2,7 • 1019 мол/м3, то на бесконечности остался бы 1 атом/м3. Приближаясь к состоянию статистического равновесия, атмосфера Луны улетучилась. В самом деле, из-за малой массы Луны вторая космическая скорость в 12 раз меньше, чем на Земле. У Марса, который тоже меньше Земли, весьма разреженная атмосфера, а у Юпитера и Сатурна, напротив, атмосферы очень плотные. При точном расчете нужно было бы рассмотреть процессы в нижних и верхних слоях атмосферы, но оценки можно сделать только при знании скоростей убегания молекул на высоте и у поверхности планеты, которые связаны со значениями ускорения свободного падения на разных высотах. Оценка времени рассеяния атмосферы, зависящего от изменений температуры, такова: при изменении T на 15 % оно меняется на два порядка. Это объясняет наличие атмосферы на Титане (шестом спутнике Сатурна) и отсутствие ее на Луне, хотя скорости убегания на этих спутниках почти одинаковы — 2,6 и 2,4 км/с соответственно. На Титане температура 70—120 К, т.е. намного ниже, чем на Луне. При такой низкой температуре только легкие газы типа гелия и водорода имеют тепловые скорости, позволяющие им убежать из атмосферы. Обнаруженная на Титане атмосфера состоит из метана и, возможно, аммиака. На Меркурии скорость убегания порядка 3,8 км/с, но близость его к Солнцу позволяет даже тяжелым молекулам иметь достаточную скорость для убегания из атмосферы, поэтому для существования атмосферы на Меркурии самые плохие условия в Солнечной системе. Рассеяние атмосферы, кроме того, сильно возрастает из-за диссоциации многоатомных молекул под действием солнечного излучения. Число Авогадро, введенное в показатель степени в распределении Больцмана, впервые определил Ж. Перрен по зависимости плотности газа от высоты. Он взял коллоидный раствор частиц гуммигута в воде, в котором при равновесии концентрация больше у основания сосуда. При боковом освещении эти частички напоминают пылинки в солнечном луче. Перрен сумел построить функцию В равновесном состоянии распределение частиц должно быть наиболее вероятным, и это осуществляется посредством многих столкновений. Если возникнут какие-то иные распределения, то при создании в системе беспорядка они исчезнут, и установится наиболее вероятное распределение. Если вывести распределение Больцмана из принципа детального равновесия, то получится та же формула, где Е — полная энергия молекулы. Это распределение названо распределением Максвелла— Больцмана, поскольку оба распределения обусловлены столкновениями молекул. Кинетическая энергия частиц, позволяющая им подниматься в силовом поле, вызвана только столкновениями. Распределение Максвелла—Больцмана соответствует наиболее вероятному распределению числа молекул в состоянии статистического равновесия. Для реальных газов этот закон применим пока можно пренебречь взаимодействием молекул на расстоянии, т. е. для достаточно разреженных газов. Ричардсон опытным путем проверил Максвеллово распределение по скоростям (1908), а Дж. Франк и Г. Герц измерили длину свободного пробега ионов водорода (1912). В то же время еще с конца 90-х гг., атомистика подвергалась непрерывным критическим атакам со стороны ряда естествоиспытателей и философствующих физиков (Оствальд, Мах, Дюгем, Гельм и др.). В своем неприятии атомистики критики исходили из следующего положения: поскольку законы термодинамики есть обобщение огромного опыта человечества, они абсолютны, поэтому обратимость во времени, связанная с тенденцией возрастания энтропии, не может объясняться механическим движением мифических микрочастиц, так как законы механики обратимы. Приведенный выше вывод распределения Максвелла по скоростям относится к одноатомным газам. Для двух- или трехатомных газов следовало бы в энергию ввести члены, характеризующие вращение или переносное движение атомов в молекуле относительно друг друга. На каждый вид вращения приходится энергия к Т/2, так что средняя энергия вращения двухатомной молекулы 2(кТ/2) = кТ, трехатомной — 3(кТ/2) = (3/2)кТ, но более трех вращений не может быть, поэтому для многоатомной молекулы энергия вращения также (3/2)кТ. Средняя энергия колебаний считается равной на каждое колебание, т.е. для молекулы водорода средняя энергия равна (3/2)kТ+ kТ+ kТ= (7/2)kТ. Здесь первое слагаемое обязано переносному движению, второе — вращательному, третье — колебательному. Из опыта следует, что она равна не (7/2)кТ, а (5/2)кТ. Это связано с тем, что оценки по классической механике в этом случае не дают верного результата — для повышения температуры на 1 °С требуется теплота, равная с. Квантовые законы меняют вид функций распределения, но они должны использоваться при низких температурах.
Поиск по сайту: |

 Кре-
Кре-
 здесь k — постоянная
здесь k — постоянная
 должны иметь одинако-
должны иметь одинако- Повернем теперь координатные оси так, чтобы новая ось
Повернем теперь координатные оси так, чтобы новая ось  совпала с направлением вектора скорости, т. е. проекции скорости в новой системе будут
совпала с направлением вектора скорости, т. е. проекции скорости в новой системе будут  От поворота осей значение
От поворота осей значение  функции
функции 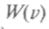 измениться не должно, поэтому
измениться не должно, поэтому  =
=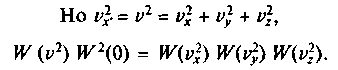
 (Можно взять и любое другое число.) Но квадраты проекций скорости на оси — величины размерные и потому не могут стоять в показателе степени без коэффициента, обеспечивающего его безразмерность.
(Можно взять и любое другое число.) Но квадраты проекций скорости на оси — величины размерные и потому не могут стоять в показателе степени без коэффициента, обеспечивающего его безразмерность. Поэтому величина
Поэтому величина  имеет ту же размерность, а обратная ей
имеет ту же размерность, а обратная ей  — размерность обратного квадрата скорости. Если взять за основу величину е = 2,718..., то среднее значение кинетической энергии не изменится и согласуется с прежним определением. Тогда искомая функция
— размерность обратного квадрата скорости. Если взять за основу величину е = 2,718..., то среднее значение кинетической энергии не изменится и согласуется с прежним определением. Тогда искомая функция  окажется пропорциональной
окажется пропорциональной 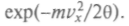 Очевидно, что нужно подобрать еще коэффициент пропорциональности, исходя из условия, что W = 1. Запишем этот коэффициент в готовом виде и получим искомое максвеллово распределение по скоростям:
Очевидно, что нужно подобрать еще коэффициент пропорциональности, исходя из условия, что W = 1. Запишем этот коэффициент в готовом виде и получим искомое максвеллово распределение по скоростям:
 не совместима с законом сохранения энергии при отдельных соударениях частиц. Графически
не совместима с законом сохранения энергии при отдельных соударениях частиц. Графически  представляется гауссовой кривой. Максимум этой кривой лежит в ок-
представляется гауссовой кривой. Максимум этой кривой лежит в ок- =
= Распределение по компонентам скорости является частным случаем нормального закона распределения Гаусса, которому подчиняются случайные ошибки при измерениях.
Распределение по компонентам скорости является частным случаем нормального закона распределения Гаусса, которому подчиняются случайные ошибки при измерениях.
 при возрастании скорости убывает быстрее, чем
при возрастании скорости убывает быстрее, чем Среднее арифметическое значение скорости находится по формуле:
Среднее арифметическое значение скорости находится по формуле: 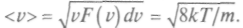 Среднее значение квадрата скорости равно
Среднее значение квадрата скорости равно  а квадратный корень из него называют средней квадратичной скоростью:
а квадратный корень из него называют средней квадратичной скоростью:
 которая может быть записана и для концентрации на определенных высотах в виде:
которая может быть записана и для концентрации на определенных высотах в виде: для концентраций, записанную через
для концентраций, записанную через  где Е — потенциальная энергия в любом поле (не обязательно в гравитационном), называют формулой Больцмана. Плотность газа убывает с высотой, но температура остается постоянной. Множитель
где Е — потенциальная энергия в любом поле (не обязательно в гравитационном), называют формулой Больцмана. Плотность газа убывает с высотой, но температура остается постоянной. Множитель  определяет вероятность того, что молекула находится на высоте h над поверхностью Земли, и задает зависимость плотности атмосферы от высоты. Отношение плотностей на высотах h и 0 равно отношению функций
определяет вероятность того, что молекула находится на высоте h над поверхностью Земли, и задает зависимость плотности атмосферы от высоты. Отношение плотностей на высотах h и 0 равно отношению функций 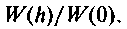 Последняя
Последняя  из них равна единице, так как ехр(0) = 1. Поэтому и
из них равна единице, так как ехр(0) = 1. Поэтому и Так как сила тяжести убывает как
Так как сила тяжести убывает как  от центра, потенциальная энергия должна убывать как первая степень расстояния. С ростом r плотность п(r) падает, т. е. и показатель степени становится меньше, тогда можно записать:
от центра, потенциальная энергия должна убывать как первая степень расстояния. С ростом r плотность п(r) падает, т. е. и показатель степени становится меньше, тогда можно записать: 
 и считая Т = 300 °С, получим:
и считая Т = 300 °С, получим: 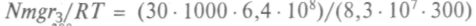 = 700 и ехр(-700) = 10-300, т.е. на бесконечности атмосфера фактически ничтожно мала.
= 700 и ехр(-700) = 10-300, т.е. на бесконечности атмосфера фактически ничтожно мала. натуральный логарифм которой равен: mgh/kT= = Nmg/RT. Зная массу коллоидных частиц из других измерений, он вычислил N. Так впервые была доказана реальность существования молекул, а статистическая физика позволила из свойств совокупности многих молекул найти свойства и характеристики отдельных частиц. Возникла возможность избежать неудобств, связанных с решением уравнений движения отдельных частиц.
натуральный логарифм которой равен: mgh/kT= = Nmg/RT. Зная массу коллоидных частиц из других измерений, он вычислил N. Так впервые была доказана реальность существования молекул, а статистическая физика позволила из свойств совокупности многих молекул найти свойства и характеристики отдельных частиц. Возникла возможность избежать неудобств, связанных с решением уравнений движения отдельных частиц.