 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Выражения (16–17) справедливы для дискретных и непрерывных случайных величин. ⇐ ПредыдущаяСтр 4 из 4
Пример 1. Дана случайная величина X:
Пользуясь неравенством Маркова, оценить вероятность того, что случайная величина X примет значение, меньшее 11? Решение.Исходя из условия будем рассуждать так: (Х<11)=Р(X=2)+Р(Х=4)+ +Р(Х=6)+Р(Х=8)+Р(Х=10)=0,1+0,2+0,25+0,15+0,15=0,85. Используя неравенство Маркова (17), получаем Р(Х<11)≥1–М(Х)/11=1–(2·0,1+4·0,2+6·0,25+8·0,15+10·0,15+12·0,15)/11=1–(0,2+0,8+1,5+1,2+1,8)/11=1–7/11=1–0,636=0,364. Р(Х<11)≥0,364. Пример 2. Сумма всех вкладов в некоторой сберегательной кассе составляет 20000000 руб., а вероятность того, то случайно взятый вклад меньше 100000 равна 0,8. Каково число вкладчиков сберегательной кассы? Решение.Пусть X – величина случайно взятого вклада, а n – число всех вкладчиков. Тогда из условия задачи следует, что М(Х)=20000000/n; Р(X<100000)=0,8, и по неравенству Маркова Р(X<100000)≥1–М(Х)/100000. Т.е. 0,8≥1–20000000/(n·100000); 20000000/(n·100000)≥0,2; 200≥n·0,2; n≤1000. Неравенство Чебышева. Вероятность того, что отклонение X от ее математического ожидания по абсолютной величине будет меньше данного положительного числа ε, ограничена снизу величиной 1–D(X)/ε2, т.е. Р(|X–M(X)|<ε)≥1–D(X)/ε2. (18) Из (18) переходом к противоположному событию можно получить: Р(|X–M(X)|≥ε)≤D(X)/ε2. (19) Пример 3. Вероятность наступления некоторого события р=0,3 в каждом из n=900 независимых испытаний. Используя неравенство Чебышева, оценить вероятность того, что событие повторится число раз, заключенное в пределах от m1=240 до m2=300. Решение.Здесь по условиям задачи имеет место биномиальный эксперимент. Следовательно: М(X)=а=пр=900∙0,3=270; ε=|240–270|=|300–270|=30; D(X)=npq=900∙0,3∙0,7=189; Р(|X–270|≤30)≥1–D(X)/ε2=1–189/302=1–0,21=0,79, т.е. Р(|X–270|≤30≥0,79. Теорема устанавливает связь в между средней арифметической Теорема Чебышева. При неограниченном увеличении числа n независимых испытаний «средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию», т.е. для любого положительного ε Р(| Смысл выражения « Р(| Подставляя в это неравенство значения M( Р(| Если в (21) взять сколь угодно малое ε>0и n®¥, то получим что и доказывает теорему Чебышева. Из рассмотренной теоремы вытекает важный практический вывод. Он состоит в том, что неизвестное нам значение математического ожидания случайной величины мы вправе заменить средним арифметическим значением, полученным по достаточно большому числу опытов. При этом, чем больше опытов для вычисления, тем с большей вероятностью (надежностью) можно ожидать, что связанная с этой заменой ошибка ( Кроме того, можно решать другие практические задачи. Например, по значениям вероятности (надежности) Р=Р(| Пример 4. Дисперсия случайной величины X равна 4. Сколько требуется произвести независимых опытов, чтобы с вероятностью не менее 0,9 можно было ожидать, что среднее арифметическое значение этой случайной величины будет отличаться от математического ожидания менее чем на 0,5? Решение.По условию задачи ε=0,5; Р(| 1–D(X)/(n∙ε2)=0.9 определяем п =D(X)/(0,1∙ε2)=4/(0,1∙0,25)=160. Если использовать утверждение, что в любом случае средняя арифметическая распределена примерно нормально, то получаем: Р(| Пример 5. Дисперсия случайной величины D(X)=5. Произведено 100 независимых опытов, по которым вычислено Решение.По условию n=100, Р(| Р(| Из соотношения 1–D(X)/(n∙ε2)=0,8 определяем ε: ε2=D(X)/(0,2∙n)=5/(0,2∙100)=0,25; ε=0,5. Пусть произведено п независимых испытаний, в каждом из которых вероятность появления некоторого события А постоянна и равна Р. Теорема Бернулли. При неограниченном возрастании числа независимых испытаний п относительная частота m/n появления события А сходится по вероятности к вероятности p события А, т.е.
где ε – сколь угодно малое положительное число. Для конечного n при условии, что P(|m/n–p|<ε)≥1–pq/(n∙ε2). (22) Каким бы малым ни было число ε при n→∞ величина дроби pq/(n∙ε2)→0, а P(|m/n–p|<ε)→1. Из теоремы Бернулли следует, что при достаточно большом числе испытаний относительная частота т/п появления события практически утрачивает свой случайный характер, приближаясь к постоянной величине p – вероятности данного события. В этом и состоит принцип практической уверенности. Пример 6. С целью установления доли брака продукции было проверено по схеме возвратной выборки 1000 единиц. Какова вероятность того, что установленная этой выборкой доля брака по абсолютной величине будет отличаться от доли брака по всей партии не более, чем на 0,01, если известно, что в среднем на каждые 10000 изделий приходится 500 бракованных? Решение.По условию задачи число независимых испытаний n=1000. p=500/1000=0,05; q=1–p=0,95; ε=0,01. P(|m/n–p|<0,01? Применяя формулу (22), получим P(|m/n–p|<0,01)≥1–pq/(n∙ε2)=1–0,05∙0,95/(1000∙0,0001)=0,527. Итак, с вероятностью не менее 0,527 можно ожидать, что выборочная доля брака (относительная частота появления брака) будет отличаться от доли брака во всей продукции (от вероятности брака) не более чем на 0,01. Пример 7.При штамповке деталей вероятность брака составляет 0,05. Сколько нужно проверить деталей, чтобы с вероятностью не менее 0,95 можно было ожидать, что относительная частота бракованных изделий будет отличаться от вероятности брака менее, чем на 0,01? Решение.По условию задачи р=0,05; q=0,95; ε=0,01. P(|m/n–p|<0,01)≥0,95; n=? Из равенства 1–pq/(n∙ε2)=0,95 находим: Контрольные вопросы 1. Какая величина называется непрерывной случайной величиной? Приведите примеры. 2. Сформулируйте определение интегральной функции распределения. 3. Перечислите свойства интегральной функции. 4. Запишите формулу вычисления вероятности попадания случайной величины в заданный интервал через интегральную функцию. 5. Дайте определение дифференциальной функции. 6. Как с помощью дифференциальной функции найти интегральную функцию? 7. Перечислите свойства дифференциальной функции . 8. Как найти вероятность попадания случайной величины в заданный интервал при помощи дифференциальной функции? 9. Назовите конкретные законы распределения непрерывных случайных величин.
Поиск по сайту: |
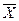 наблюдаемых значений случайной величины X и М(X)=а.
наблюдаемых значений случайной величины X и М(X)=а.  –а|<ε)=1. (20)
–а|<ε)=1. (20)
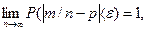
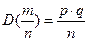 , неравенство Чебышева для случайной величины m/n будет иметь вид:
, неравенство Чебышева для случайной величины m/n будет иметь вид: