 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приклади розв'язку задач ⇐ ПредыдущаяСтр 2 из 2
 Задача 1(приклад постановки прямої задачі). Задача 1(приклад постановки прямої задачі).
В електричному колі, наведеному на рис.8 , електрорушійна сила джерела Е=50В, а опори резисторів дорівнюють R1 =10 Ом, R2=20 Ом, R3 =20Ом. Визначити значення струмів І1, І2, І3. Розв’язання 1) Для розв’язку задачі використовуємо еквівалентне перетворення:
2) Визначаємо еквівалентний опір схеми: 3) Застосовуємо закон Ома для замкненого кола для визначення струму на нерозгалуженій ділянці кола: 4) Знаходимо напругу на ділянці аb: 5) За законом Ома визначаємо струм через резистор з опором R2: 6) За першим законом Кірхгофа знаходимо струм через резистор R3:. 7) Правильність розв’язку задачі перевіряємо за допомогою балансу потужності:
Одержуємо, що енергія джерела ЕРС дорівнює енергії, яка виділяється на резисторах. Це є доказом правильності розв’язку задачі. Задача 2(приклад зворотної задачі). Для електричного кола (рис.8) задані значення опорів R1 =10 Ом, R2=5 Ом, R3 =10 Ом і струму І3 = 2А. Визначити струми І1 , І2 та ЕРС джерела. Розв’язання 1) Визначаємо напругу на ділянці аb: 2) Для розрахунку струму через резистор R2 скористаємося законом Ома для ділянки кола: 3) Для знаходження струму І1 застосуємо перший закон Кірхгофа: 4) Визначаємо падіння напруги на резисторі R1: 5) Знаходимо ЕРС джерела за другим законом Кірхгофа: 6) Для перевірки правильності розв’язку задачі складаємо баланс потужності:
Рівність лівої та правої частин рівняння балансу є доказом правильності розв’язання задачі.

Задача 3.Для електричного кола, зображеного на рис.3, з такими параметрами: E1=120B, E2=20B, E3= 80B, R1 = R2=2 Ом, R3 =40 Ом, R3 =50 Ом, визначити всі струми за допомогою методу Кірхгофа. Розв’язання Спочатку проводимо структурний аналіз: визначаємо кількість вузлів і незалежних контурів. Потім довільно обираємо напрямки струмів в гілках і напрямки обходу контурів (за годинниковою чи проти годинникової стрілки). 1) Кількість вузлів n=2, тому складаємо одне рівняння за першим законом Кірхгофа для вузла 2:
2) Так як кількість незалежних контурів l=3, то складаємо три рівняння за другим законом Кірхгофа:
В результаті маємо систему чотирьох рівнянь, в якій кількість невідомих дорівнює кількості рівнянь. 3) Враховуючи початкові дані, розв’язуємо систему відносно струмів:
Розв’язання цієї системи рівнянь дає значення струмів:
Від’ємне значення струму показує, що дійсний напрямок струму протилежний.
Задача 4. Визначте, згідно нижче вказаної схеми, Розв'язання.
цього розіб'ємо дану схему на каскади. Отри- маємо
2.Далі розглянемо каскад ди 3.Звідси визначимо загальний опір кола 1. Нам відомо силу струму на п’ятому резисторі, а так як четвертий та п’ятий резистори з’єднано послідовно, то і сила струму на них буде рівною 2. Визначимо значення напруги на каскаді 3. Каскади 4. Визначимо силу струму каскаду 5. Так як 6. Для визначення
Поиск по сайту: |
 .
. .
.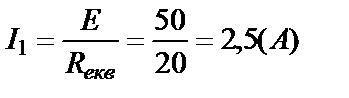 .
.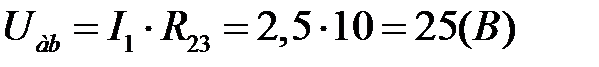 .
.



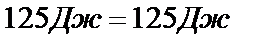
 .
. .
. .
. .
.
 10
10 .
. .
.
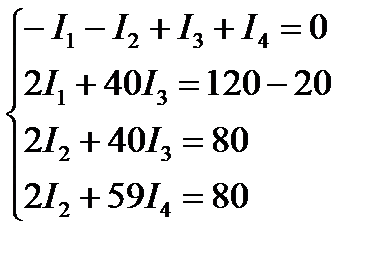



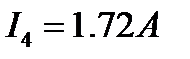 .
. ,
,  ,
,  , якщо
, якщо  ,
,  ,
,  ,
, 


 1. Визначимо загальний опір даної схеми. Для
1. Визначимо загальний опір даної схеми. Для , бо дані каскади з'єдна-
, бо дані каскади з'єдна-
 но послідовно.
но послідовно. в якому каска-
в якому каска- та
та  з'єднано паралельно, тому:
з'єднано паралельно, тому:  . Так як у каскадах
. Так як у каскадах 
 ,
, 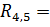
 ; тому звідси
; тому звідси 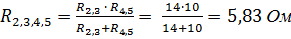 .
.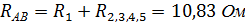 .
. , тобто
, тобто 
 .
. =
= 

 , звідси
, звідси 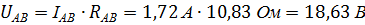
 розглянемо, що нам відомо на каскаді
розглянемо, що нам відомо на каскаді  , тому скориставшись законом Ома для ділянки кола, визначимо
, тому скориставшись законом Ома для ділянки кола, визначимо 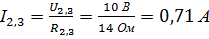 . Проте нам відомо, що резистори в даному каскаді з’єднано послідовно, а це означає, що струм каскаду та кожного із резисторів однаковий, тому
. Проте нам відомо, що резистори в даному каскаді з’єднано послідовно, а це означає, що струм каскаду та кожного із резисторів однаковий, тому 