 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Исследование зависимости скорости звука от плотности исследуемой жидкости ⇐ ПредыдущаяСтр 3 из 3
В жидкостях звук распространяется в виде объемных волн разряжения-сжатия (продольные волны), причем процесс этот обычно адиабатический, т.е. изменение температуры в УЗ волне не успевает выравниваться. Скорость распространения УЗ волн в жидкостях выражается следующим уравнением:
где: Следовательно, измеряя тем или иным способом скорость распространения УЗ волны в данной среде и считая коэффициент адиабатической сжимаемости постоянным, можно легко определить плотность среды. Однако коэффициент адиабатической сжимаемости достаточно сложно вычислить. Уменьшение амплитуды и интенсивности УЗ волны по мере ее распространения в заданном направлении, т.е. затухание звука, обуславливается, расхождением фронта волны с удалением от источника, рассеянием и поглощением звука, которое характеризуется коэффициентом поглощения a. Интенсивность УЗ при прохождении расстояния L убывает по экспоненциальному закону и описывается формулой, которая имеет следующий вид:
I = I 0 ·exp(-2·α·L),
где: I 0 – начальная интенсивность, Вт/м2. В жидкостях скорость звука, как правило, уменьшается с ростом температуры. Исключением из этого правила является вода, в которой скорость звука при увеличении температуры растет. Имеется аналогия и в измерении плотности газообразных и твердых веществ. Плотность уменьшается с ростом температуры (вследствие температурного расширения и увеличивается с ростом давления). Исключение составляет вода – ее плотность имеет максимум при 4°С и уменьшается как с повышением, так и понижением температуры. Время прохождения импульса определяется по следующим формулам:
∆t = T = 1/F Г , (3.3)
где: F Г =40 МГц – частота генератора.
t = N·∆t (3.4)
Общее время, которое понадобится УЗ импульсу для прохождения через сосуд, выражается следующей формулой:
t общ = 2·( t ж+ t тр+ t пр),
где: t ж – время, затрачиваемое на прохождение УЗ импульса через жидкость; t тр – время, затрачиваемое на прохождение УЗ импульса через стенку сосуда; t пр – время, затрачиваемое на прохождение УЗ импульса через протектор.
Скорость распространения ультразвука в исследуемой среде будет определяться из выражения:
где L – расстояние между стенками сосуда.
В лабораторной работе проводится определение плотности растворов состоящих из: · воды и этилового спирта; · воды и сахара; · воды и поваренной соли.
Поиск по сайту: |
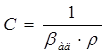 ,
, – коэффициент адиабатической сжимаемости жидкости.
– коэффициент адиабатической сжимаемости жидкости. ,
,