 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эквивалентные схемы замещения диэлектрика с потерямиСтр 1 из 3Следующая ⇒
Чтобыизучить диэлектрические потери какого –либо материала, необходимо измерить ряд параметров конденсатора с этим материалом в цепи переменного напряжения. Конденсатор с исследуемым диэлектриком, имеющий емоксть С, рассеиваемую мощность Р и угол сдвига фаз между током и напряжением Паралелльная схема замещения диэлектрика с потерями и векторная диаграмма тококв в ней представлены на рисунке 4.2, из которого видно, что активная составляющая тока
где Z – полное сопротивление, Из треугольников токов (рисунок 4.2, б) следует, что
Последовательная эквивалентная схема замещениядиэлектрика с потерями и соответствующие ей векторная диаграмма напряжений и треугольник сопротивлений, представленные на рисунке 4.3, показывают, что активная составляющая напряжения Uaсовпадает по фазе с током I, а реактивная составляющая U, отсстает от тока на угол 90о.
Если треугольник напряжений (см. рисунок 4.3, б) разделить на постоянную величину тока I, получим треугольник сопротивлений (рис. 4.3, в), из которого имеем:
Величину рассеиваемой мощности P при постоянномнарпяжении можно определить с помощью закона Джоуля-Ленца:
При переменном напряжении эта величина в общем виде равна
Для параллельной схемы замещения, используя ранее рассмотренные выражения и соответствующую векторную диаграмму, получим:
где Для последовательной схемы замещения, используя треугольник напряжений (рис. 4.3, в) получим:
Поиск по сайту: |
заменим эквивалентной схемой, в которой к идеальному конденсатору активное сопротивление подключено либо параллельно – паралелньная эквивалентная схема замещения, либо последовательно – последовательная эквивалентная схема замещения. Эти эквивалентные схемы замещения диэлектрика с потерями должны быть выбраны так, чтобы рассеиваемая в них активная мощность была равна мощности Р, выделяющейся в конденсаторе с исследуемым диэлектриком, а ток опережал бы напряжение на угол 
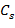и R, 
и r.
совпадает по фазе с напряжением U, а реактивная составляющая тока 
опережает напряжение на угол, равный 90о. Значения соответствующих токов равны
, 
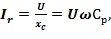
; xc–реактивное (емкостное) сопротивление конденсатора с диэлектриком, 
( 
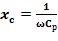– угловая частота).
.
.
.
,
.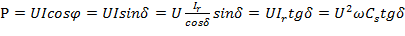