 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предпосылки создания теории электролитической диссоциации. Изотонический коэффициентСтр 1 из 3Следующая ⇒
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Химия»
«УТВЕРЖДАЮ» Заведующий кафедрой «Химия» Профессор, д.т.н. Ю.Перелыгин «____»______________ 2013 г.
ТЕКСТ ЛЕКЦИИ № 6
по дисциплине «Химия» по специальности 200100 «Приборостроение»
Тема № 4. Растворы. Дисперсные системы Занятие №3. Растворы электролитов
Текст лекции обсужден на заседании ПМК №__ кафедры «Химия» «___»____________ 2013 г., протокол №_____
Г. Пенза
Содержание Введение 1. Предпосылки создания теории электролитической диссоциации. Изотонический коэффициент. 2. Механизм электролитической диссоциации. 3. Степень электролитической диссоциации. 4. Слабые электролиты. Закон разбавления Оствальда. 5. Сильные электролиты. Активность электролитов. 6. Кислоты, основания и соли с точки зрения теории электролитической диссоциации. 7. Реакции ионного обмена. Литература: 1. 1. Коровин Н. В. Общая химия. Учебник. – М.: Высшая школа, 1998. – с. 210 - 224. Учебно – материальное обеспечение: 1. Мультимедийный проектор. 2. Установка для испытания электропроводности растворов; растворы электролитов и неэлектролитов.
Цель занятия: Знать: 1.Теория электролитической диссоциации. Особенности применения законов идеальных растворов к растворам электролитов. Изотонический коэффициент. 2. Степень диссоциации. Уравнение связи между изотоническим коэф-фициентом и степенью диссоциации. Сильные и слабые электролиты. Константа диссоциации. Уравнение связи между константой диссоциации и степенью диссоциации – закон разбавления Оствальда. 3. Ступенчатая диссоциация многоосновных кислот и многокислотных гидроксидов в растворе. Диссоциация амфотерных электролитов. 4. Смещение равновесия реакций обмена для электролитов. Примеры реакций. Ознакомиться:с буферными растворами.
Организационно-методические указания: 1.Проверить наличие обучаемых и их готовность к занятиям, устранить недостатки. 2.Объявить тему и цель занятия, учебные вопросы, литературу. 3.Обосновать необходимость изучения данной темы на примерах применения электролитов в приборостроении. 4.Рассмотреть учебные вопросы с применением кадров презентации и установки для испытания электропроводности растворов. 5.По каждому учебному вопросу и в конце занятия подвести итоги. 6.В конце занятия выдать задание на самоподготовку. ВВЕДЕНИЕ На предыдущей лекции мы познакомились с общими (коллигативными) свойствами растворов, изучили основные закономерности, описывающие поведение этих растворов. Справедливость этих закономерностей подтверждается результатами многих экспериментов. Однако, имеются вещества, растворы которых сильно отклоняются от всех рассмотренных законов. К подобным веществам относятся соли, кислоты и щелочи. Изучению этих веществ, получивших название электролитов, и посвящена настоящая лекция.
Предпосылки создания теории электролитической диссоциации. Изотонический коэффициент. Еще в конце XIX века было установлено, что для солей, кислот и щелочей реальное или наблюдаемое осмотическое давление, понижение давления пара, изменение температур кипения и замерзания всегда больше, чем это отвечает концентрации раствора. Так, например, для 0,2 н. раствора хлорида калия реальное понижение температуры замерзания в 1,81, то есть почти в два раза больше, чем вычисленное по формуле Рауля. (см. табл.1). Табл. 1. Значение коэффициента i для 0,2 н. растворов некоторых солей
Когда для указанного раствора KCLизмерили повышение температуры кипения , эта величина также оказалась больше вычисленной по формуле в такое же число раз. Во столько же число раз и осмотическое давление этого раствора оказалось больше теоретической величины. Как Вы уже знаете, величина осмотического давления для разбавленных растворов подчиняется закону Вант-Гоффа: Оказалось, что для растворов солей наблюдаемые понижения давления пара, изменение температур кипения и замерзания, осмотическое давление всегда больше вычисленных по формулам в i раз:
Δtкип = i Δtзам = i i – изотонический коэффициент или коэффициент Вант-Гоффа
Практически i определяют, сравнивая реально наблюдаемые и вычисленные по формулам значения Δtзам : i = Вернемся к нашей таблице. В ней приведены значения изотонических коэффициентов, найденные Вант-Гоффом для двудецинормальных растворов некоторых солей. Из таблицы мы видим, что изотонический коэффициент i больше единицы и для разных солей имеет различные значения: для Итак, соли, кислоты, основания, растворяясь в воде, дают «увеличенные» по сравнению с теоретическими значения рассмотренных величин. Как это объяснить? Мы видим, что во все наши формулы входит произведение постоянных величин и обязательно входит концентрация раствора. А концентрация раствора, будь то молярная концентрация (как в формуле Так как и зависят от концентрации растворов, шведский химик Аррениус в 1887 году предположил, что молекулы солей, оснований и кислот при растворении распадаются на ионы, и общее число частиц в растворе увеличивается. Следующий вопрос, который возникает при этом: на какие частицы распадаются соли, основания и кислоты? Когда Аррениус искал ответ на этот вопрос, уже было известно, что водные растворы солей, оснований и кислот обладают еще одной особенностью: они проводят электрический ток. При этом сухие соли, основания и кислоты тока не проводят, чистая вода сама по себе также обладает очень плохой проводимостью. Как вы уже знаете из школьного курса, вещества, растворы или расплавы которых проводят электрический ток, называются электролитами. Электролиты – проводники II рода, электрический ток в них переносится ионами. Эти сведения были известны еще до Аррениуса, но считалось, что электролиты распадаются на ионы только под действием электрического тока. Аррениус же впервые обратил внимание на тесную связь между способностью растворов солей кислот и оснований проводить электрический ток и отклонениями свойств этих растворов от законов Рауля и Вант-Гоффа. Им была выдвинута гипотеза о том, что молекулы электролитов распадаются на ионы уже при растворении, еще до пропускания электрического тока. Эти предположения в дальнейшем были развиты в стройную теорию, получившую название теории электролитической диссоциации (ТЭД). Электролитическая диссоциация – это процесс распада электролита на ионы под действием полярных молекул растворителя. Первое положение ТЭД При растворении в воде электролиты распадаются на положительно заряженные ионы – катионы и отрицательно заряженные ионы – анионы. Например, диссоциацию KCl и MgCl2 можно выразить уравнениями: KCl = 1 частица 2 иона MgCl2 = 1 частица 3 иона
Вот теперь мы можем объяснить отклонения от законов Рауля и Вант-Гоффа. В качестве примера мы рассматривали понижение температуры замерзания для хлорида калия. Это понижение было в 1,81 раза больше рассчитанного по формуле Δtзам = K Точно также в разбавленном растворе хлорида магния понижение температуры замерзания оказывается в 2,79 раз больше, чем вычисленное по формуле Δtзам = K Рассмотренные примеры позволяют выяснить физический смысл изотонического коэффициента. Изотонический коэффициент i – это отношение всех частиц, находящихся в растворе, к числу частиц, введенных в раствор. Однако, теория Аррениуса не сразу получила широкое признание. Особое недоумение вызывало у современников Аррениуса его предположение о диссоциации в растворе некоторых солей, например, хлорида натрия. Если хлорид натрия распадается в воде на натрий и хлор – говорили они – значит, раствор поваренной соли должен пахнуть хлором, а образовавшийся хлорид натрия должен бурно реагировать с водой. Почему этого не происходит? Ответом на этот вопрос служит второе положение теории электролитической диссоциации. Второе положение ТЭД Ионы по своим свойствам отличаются от атомов и молекул. Однако, теория Аррениуса не учитывала всей сложности явлений в растворах. В частности, она рассматривала ионы как свободные, независимые от молекул растворителя частицы. Теории Аррениуса противостояла химическая или гидратная теория растворов Менделеева. Как вы помните, в основе этой теории лежит представление о взаимодействии растворенного вещества с растворителем. В преодолении кажущегося противоречия обеих теорий большая заслуга принадлежит русскому ученому И.А. Каблукову. Он впервые высказал предположение о гидратации ионов. Развитие этой идеи привело к дальнейшему объединению теории Аррениуса и Менделеева.
Поиск по сайту: |
 . Чтобы распространить этот закон на растворы с «ненормальным» осмотическим давлением, Вант-Гофф ввел в уравнение поправочный коэффициент, показывающий, во сколько раз осмотическое давление данного раствора больше нормального. Этот коэффициент был назван изотоническим и обозначался буквой i. Коэффициент i определялся для каждого раствора экспериментальным путем – например, по понижению давления пара, или по понижению температуры замерзания, или по повышению температуры кипения.
. Чтобы распространить этот закон на растворы с «ненормальным» осмотическим давлением, Вант-Гофф ввел в уравнение поправочный коэффициент, показывающий, во сколько раз осмотическое давление данного раствора больше нормального. Этот коэффициент был назван изотоническим и обозначался буквой i. Коэффициент i определялся для каждого раствора экспериментальным путем – например, по понижению давления пара, или по понижению температуры замерзания, или по повышению температуры кипения. .
. E
E 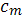 ,
, .
. i
i  для
для 
 ), или моляльность (как в формуле Δtзам = i
), или моляльность (как в формуле Δtзам = i  i
i  2;
2;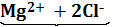 i
i  . Но теперь мы видим, что из одной условной молекулы
. Но теперь мы видим, что из одной условной молекулы  образуется вдвое большее число частиц, то есть концентрация частиц повышается вдвое. Поэтому и понижение температуры замерзания в растворе
образуется вдвое большее число частиц, то есть концентрация частиц повышается вдвое. Поэтому и понижение температуры замерзания в растворе  , так как число частиц в растворе
, так как число частиц в растворе  в три раза больше, чем если бы хлорид магния находился в растворе в виде условных молекул.
в три раза больше, чем если бы хлорид магния находился в растворе в виде условных молекул.