|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫСтр 1 из 3Следующая ⇒
Федеральное агентство по образованию и науке Российской Федерации Российский государственный университет Нефти и газа им. И.М. Губкина
В.В. ФЕДОРИШИН, Ю.В. РЕПИНА, Н.В. СИНИЦЫНА Исследование резонансных явлений (резонанса напряжений и резонанса токов)
Лабораторная работа №2 по курсу: “Электротехника и основы электроники”
Москва 2013 Федеральное агентство по образованию и науке Российской Федерации Российский государственный университет Нефти и газа им. И.М. Губкина Кафедра теоретической электротехники и электрификации Нефтяной и газовой промышленности
В.В. ФЕДОРИШИН, Ю.В. РЕПИНА, Н.В. СИНИЦЫНА Исследование резонансных явлений (резонанса напряжений и резонанса токов) Повышение коэффициента мощности
Лабораторная работа №2 по курсу: “Электротехника и основы электроники”
Под редакцией проф. Ершова М.С.
Москва 2013
УДК 621.3.01
В.В. Федоришин, Ю.В.Репина, Н.В. Синицына. Исследование резонансных явлений (резонанса напряжений и резонанса токов). Повышение коэффициента мощности. Лабораторная работа №2. -М.: РГУ нефти и газа им. И.М. Губкина, 2013г., 32 с.
В работе изложены краткие сведения по теории резонансных явлений и изучаются способы экспериментального определения резонансов напряжений и токов, а также дается методика обработки и анализа полученных результатов. Кроме того, в лабораторной работе рассматриваются способы повышения коэффициента мощности узлов электрической нагрузки. Лабораторная работа предназначена для студентов факультетов ГГНиГ, РНиГМ, ПСиЭСТТ, ИМ, ХТиЭ, АиВТ, изучающих курс: “Электротехника и основы электроники”.
Рецензенты профессор, д.т.н. Егоров А.В.
профессор, д.т.н. Портнягин Н.Н.
ã Российский Государственный университет нефти и газа им. И.М. Губкина, 2013 г. ЦЕЛЬ РАБОТЫ Цель данной лабораторной работы - изучение резонансных явлений (резонанса напряжений и резонанса токов) и их практическое применение в промышленности, исследование способов повышения коэффициента мощности установок. В процессе выполнения лабораторной работы студенты должны усвоить особенности определения и расчета основных величин в цепях переменного синусоидального тока (сопротивлений, токов, напряжений, мощностей, коэффициента мощности, фазового сдвига), научиться строить резонансные кривые и векторные диаграммы напряжений и токов.
ОСНОВЫ ТЕОРИИ Режим работы электрической цепи, включающей в себя катушки индуктивности и конденсаторы, для которой эквивалентное (входное) реактивное сопротивление или эквивалентная (входная) реактивная проводимость равна нулю, называется резонансным режимом. XЭ=0, BЭ=0. Электрическая цепь в резонансном режиме ведет себя как чисто активное сопротивление по отношению к внешней цепи, то есть напряжение и ток на входе цепи находятся в фазе (совпадает по фазе). Различают два вида резонанса - резонанс напряжений и резонанс токов.
2.1. Резонанс напряжений Резонанс, возникающий в цепи (рис. 1), где катушка индуктивности и конденсатор включены последовательно, называется резонансом напряжений. Полное комплексное эквивалентное сопротивление такой цепи: ZЭ = RЭ + jXЭ = RК + jXК - jXС = RК + j(XК - XС) = RК+ j(w×L - 1/w×C). (1)
Рис. 1. Электрическая схема для исследования резонанса напряжений Приравнивая нулю мнимую часть(ZЭ = 0), определим условие резонанса напряжений: XЭ = XК – XС = wР×L - 1/wР×С = 0,т.е. XК = XС или wР×L = 1/wР×С,(2) где wР - резонансная частота. Из выражения (2) следует, что резонанса напряжений можно добиться меняя частоту напряжения источника питания, либо величину индуктивности или емкости. Первый случай называется частотным резонансом, два других - параметрическими. Проведя анализ выражения (2), запишем значения параметров, при которых наступит резонанс напряжений: Индуктивное (или емкостное) сопротивление в момент частотного резонанса называется характеристическим сопротивлением, обозначается буквой r и определяется из выражений (2) и (3).
Сила тока, протекающего в цепи в момент резонанса, будет максимальной, и равной: Падения напряжений на катушке и конденсаторе практически будут равны между собой: ZК×IР @ XС×IР, UК @ UС. (6) Напряжения на конденсаторе и катушке при определенных значениях емкости достигают своих максимальных значений UC MAX и UК MAX, которые определяются по формулам: Теоретические исследования данных формул показывают,что напряжение на конденсаторе достигает UС MAX при С¢< СР и UС MAX> UК MAX. Если считать катушку индуктивности идеальной (т.е. RК=0), то напряжения на катушке и конденсаторе будут равны между собой: XК×IР =XС ×IР, UК = UС ,где UК = UХк = XК× IР. (7) Идеальный резонанс напряжений эквивалентен короткому замыканию входных зажимов цепи (т.к. IP=U/RК=U/0=¥). Отношения напряжения на катушке индуктивности (или конденсаторе) к входному напряжению в режиме резонанса называют добротностью контура:
Добротность (q) показывает во сколько раз напряжение на катушке индуктивности (или конденсаторе) выше входного напряжения и зависит от параметров катушки и конденсатора. Запишем второй закон Кирхгофа для данной цепи (рис. 1) в комплексной форме: Представим выражение (9) на комплексной плоскости для трех случаев: до резонанса (UК<UС);в момент резонанса (UК @UС); после резонанса (UК>UС),то есть построим векторные диаграммы напряжений (рис. 2).
Рис.2. Векторные диаграммы напряжений. Как следует из векторной диаграммы напряжений (рис.2) в режиме резонанса напряжений, вектор входного тока IPсовпадает по фазе с вектором входного напряжения U, т.е. фазовый сдвиг между этими векторами:
В режиме резонанса эквивалентная реактивная мощность всей цепи равна:
а эквивалентная полная мощность цепи становится чисто активной мощностью:
2.2. Резонансные кривые резонанса напряжений В данной работе исследуется параметрический резонанс за счет изменения емкости в цепи. При исследовании параметрического резонанса напряжений строятся резонансные кривые I(C), UК(C), UС(C), jЭ(C), cosjЭ(C) - (рис. 3), согласно следующим формулам:
Рис. 3. Резонансные кривые тока I, напряжения на реальной катушке индуктивности UК, напряжения на конденсаторе UС, фазового сдвига jЭ, коэффициента мощности cos jЭ от емкости конденсатора С при исследовании резонанса напряжений.
В электроэнергетических установках (устройствах) в большинстве случаев резонанс напряжений - явление нежелательное, связанное с возможным возникновением перенапряжения, т.е. напряжением, в несколько раз превышающим рабочее (номинальное) напряжение установки (например, на обмотках трансформаторов, двигателей и т.д.). Но в радиотехнике, телефонии, телеметрии, автоматики и т.п. - явление резонанса напряжений широко используется (например, для настройки цепи на определенную частоту, в резонансных фильтрах и т.д.).
2.3. Резонанс токов Резонанс возникающей в цепи (рис. 4), где катушка индуктивности и конденсатор включены параллельно, называется резонансом токов.
Рис. 4. Электрическая схема для исследования резонанса токов.
Полная комплексная эквивалентная проводимость такой цепи:
Приравнивая мнимую часть выражения (13) к нулю, определяем условие резонанса токов:
т.е. где wР- резонансная частота. Сила тока на входе резонансного контура в момент резонанса будет минимальной и равной:
Токи, протекающие в параллельных ветвях практически равны между собой: IК @ IС,т.к. YК×U @BС×U,где Если считать катушку индуктивности идеальной (RК = 0), тогда токи в катушке и конденсаторе будут равны между собой: I¢К=I¢С, т.к. Y¢К ×U=BС ×Uи B¢К ×U=BС ×U,где
Идеальный резонанс токов эквивалентен разрыву (холостому ходу) в цепи (т.к. IP=G¢К×U=0×U=0). Запишем первый закон Кирхгофа для исследуемой цепи в комплексной форме: I = IК +IC = YК×U + YC×U = (GК –jBК)×U + jBC×U= = GК×U –jBК×U + jBC×U = IRк + IХк + IC , (18) где IRк = GК×U - активная составляющая тока катушки; IХк = –jBК×U - реактивная составляющая тока катушки, а IRк + IХк = IК Представим первый закон Кирхгофа (18) на комплексной плоскости для трех случаев: до резонанса (IК >IС);в момент резонанса (IК @ IС); после резонанса (IК >IС),т.е. построим векторные диаграммы токов (рис. 5). Как следует из векторной диаграммы токов (рис. 5), в режиме резонанса токов, вектор входного напряженияUсовпадает по фазе с вектором входного тока IP = I, т.е. фазовый сдвиг между этими векторами: jЭ = yU - yI = 0° В режиме резонанса эквивалентная реактивная мощность всей цепи равна:QЭ = QК – QС = BК× U2 - BС×U2 = 0, (19) а эквивалентная полная мощность цепи
Рис. 5. Векторные диаграммы токов.
2.4. Резонансные кривые резонанса токов
При исследовании параметрического резонанса токов строятся резонансные кривые IС(С), IК(С), I(С), jЭ(С), cosjЭ(С) (рис.6).
Рис. 6. Резонансные кривые тока конденсатора IС, тока реальной катушки индуктивности IК, входного тока I, фазового сдвига jЭ, коэффициента мощности cos jЭ от емкости конденсатора С при исследовании резонанса токов.
Резонансные кривые (рис.6) построены согласно следующим выражениям: IС(C) = BС ×U = w×C×U,
Отметим, что резонанс токов, в отличие от резонанса напряжений (вызывающего перенапряжение в электрических установках) безопасен для электроэнергетических установок и в частности может быть использован для компенсации реактивной мощности в них. Большие токи в цепях при резонансе токов возникают лишь в том случае, если созданы большие реактивные проводимости ветвей, т.е. установлены большие батареи конденсаторов или мощные реактивные катушки.
2.5. ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ Коэффициент мощности (cos j) – один из основных энергетических показателей электротехнических установок. Повышение cos j приводит к снижению потерь при транспортировке электрической энергии от источника к приемникам, а также к увеличению коэффициента полезного действия (КПД) установок. Как известно, коэффициент мощности можно определить из треугольника мощностей по формуле:
где j - сдвиг фаз между векторами напряжения U и тока I; S - полная мощность цепи; Р – активная мощность цепи; QL – индуктивная мощность, QС – емкостная мощность; Q=QL-QC=U×I×sinj=U×IX - реактивная мощность цепи, а IX=I×sinj - реактивная составляющая реального тока I (этот ток просто называют реактивным током). Как следует из формулы (21) для повышения cos j необходимо снижать реактивную мощность Q, однако в двигателях переменного тока (асинхронных двигателях) для получения вращающего момента используется взаимодействие вращающего поля статора и проводников с током ротора; следовательно, таким машинам необходим переменный намагничивающий реактивный ток IX (т.е. реактивная мощность Q=U×IX) для создания вращающегося магнитного поля, а это ухудшает коэффициент мощности cos j промышленных установок предприятий. Низкое значение коэффициента мощности вызывает неполное использование мощности генераторов, линий электропередач и трансформаторов. Они бесполезно загружаются реактивным током IX. Наличие реактивного тока IX обуславливает увеличение потерь DРЛИН в проводах при передаче электрической энергии. Эти потери:
складываются из потерь при передаче активного тока IR ибесполезных потерь при передаче реактивного тока IX. Последние вызываются перемещениями энергии из магнитных полей двигателей на электрические станции и генераторы и обратными перемещениями. Использования резонанса токов дает возможность разгрузить источник энергии и передающие устройства от этих бесполезных колебаний электрической энергии, а следовательно, и от реактивного тока IX, замкнув колебания электрической энергии в резонансном контуре, образуемом конденсаторами с емкостью С и катушкой с индуктивностью L. Практически эта разгрузка осуществляется включением параллельно двигателям с эквивалентными параметрами (RПР, ХПР) батареи конденсаторов с емкостью С (см. рис. 7).
Рис.7. Схема и векторная диаграмма компенсации сдвига фаз. Реактивная (емкостная) мощность QC последних для полной компенсации сдвига фаз j должна быть равна реактивной (индуктивной) мощности двигателей QL = U×Iпр×sin j . В большинстве случаев осуществляется неполная компенсация сдвига фаз, так как наличие небольшого реактивного тока IX при cos j³ 0,95 значений не имеют потому что Обычно задано то значение cos j, которое должна иметь электротехническая установка после компенсации; если исходные значения тока приемника IПР и его cos jПР известны (как правило эти значения указываются в паспортных данных электротехнических установок), то необходимое значение емкости С батареи конденсаторов определяется на основании следующего. Для того чтобы уменьшить сдвиг фаз jПР до значения j необходимо как показывает векторная диаграмма (см. рис. 7), уменьшить результирующий реактивный ток установки на величину IXпр-IX; здесь Активный ток IR связан с реактивным IX простым соотношением
Активный ток при компенсации остается без изменения IRпр= IR=const (см. рис.7) Выполняя соответствующие подстановки, можно выразить искомую разность реактивных токов следующим образом:
Этой разности должен быть численно равен емкостной ток IС необходимый для компенсации:
Так как согласно закону Ома емкостной ток связан с емкостью соотношением: следовательно, необходимая для компенсации емкость:
Улучшение коэффициента мощности (cos j) посредством включения конденсаторов (батареи конденсаторов) именуется искусственным улучшением коэффициента мощности в отличие от естественного улучшения, получаемом при полном использовании мощности двигателей и установки двигателей не потребляющих реактивный ток (синхронных двигателей). Пример. Согласно паспортным данным РПР = 500 кВт, UПР = 10 кВ, При данных параметрах электротехнической установки ток, потребляемый из сети Для получения той же активной мощности приемника РПР (для совершения той же полезной работы) при повышении коэффициента мощности до cos j = 1, ток потребляемый из сети будет равен
Следовательно, при повышении коэффициента мощности электротехнической установки до cos j = 1, ток, потребляемый из сети, уменьшается в 1,25 раза, что естественно приводит к уменьшению потерь в линиях электропередач, (см. формулу 22) и повышению КПД электротехнических установок, а также существенно разгружает работу источников и линий электропередач.
ДОМАШНЕЕ ЗАДАНИЕ 3.1. Проработать литературу по данному разделу. 3.2.Подготовить бланк отчета, в котором дать перечень пунктов лабораторного задания. К каждому пункту начертить электрическую схему для проведения исследований и таблицу для записи экспериментальных и расчетных данных. 3.3.Записать математические выражения (формулы) для проведения расчетов полученных экспериментальных данных. 3.4.Ответить на контрольные вопросы.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ. 4.1.Экспериментальным путем определить параметры реальной катушки индуктивности (RК,XК). 4.2.Экспериментальным путем исследовать резонанс напряжений. 4.3. Экспериментальным путем исследовать резонанс токов. Изучить особенности работы электрической цепи в резонансных режимах. ЛАБОРАТОРНОЕ ЗАДАНИЕ. 5.1. Определить параметры реальной катушки индуктивности (RК=R18,XК). Для этого необходимо собрать схему, изображенную на рис. 9, где представлена исследуемая катушка индуктивности с параметрами XК и RК= R18. Монтажная схема рис. 8 должна соответствовать принципиальной схеме исследования рис.9. После проверки электрической схемы преподавателем включить исследуемую цепь под напряжение. Цепь питается от регулируемого источника переменного синусоидального напряжения, расположенного в блоке 10, напряжение питания устанавливается с помощью переключателя тумблера SA70 и Латра SA71 и SA72. Перед включением питания необходимо убедиться, что ручка регулятора источника питания лабораторного трансформатора (ЛАТРа) находится в крайнем правом положении и тумблер переключения пределов регулирования напряжения ЛАТРа SA70 –в положении «100←0». Подачу питания произвести в следующей последовательности: · Установить автоматический выключатель (QF1,QF2,QF3), расположенный слева внизу стенда, в верхнее положение. · При помощи Задатчикавыбрать профиль отображения приборов L2 (см. лабораторную работу №1). · Для подключения питания к исследуемой схеме в блоке 3 установить в верхнее положение тумблер SA3 в блоке 3, подключив тем самым питание от ЛАТРа к блоку 3. Установить входное напряжение UВХ=110 В (по вольтметру pV11). Для этого изменять напряжение на выходе ЛАТРа TV2 переключателями: SA70 – с шагом 10 В и SA72 - с шагом 1÷2В в блоке 10. Измерить ток I в цепи, напряжение на входе UВХ и активную мощность P цепи. Результаты измерений занести в таблицу 1. Таблица 1.
После окончания эксперимента выключить тумблер SA3 в блоке 3 (перевести в нижнее положение), ручки регуляторов напряжения SA71 и SA72 перевести в начальное положение «0».
Рис.8. Схема экспериментального исследования параметров катушки индуктивности и резонансных режимов.
Рис.9.Принципиальная схема экспериментального определения параметров катушки индуктивности.
Поиск по сайту: |
 - резонансная частота,
- резонансная частота,  - резонансная индуктивность,
- резонансная индуктивность,  - резонансная емкость, где w - частота источника питания.(3)
- резонансная емкость, где w - частота источника питания.(3)  (4)
(4) (5)
(5)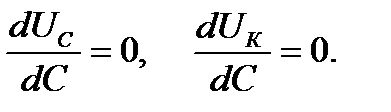
 либо
либо (8)
(8) (9)
(9) где:
где:  - начальная фаза входного напряжения;
- начальная фаза входного напряжения;  - начальная фаза входного тока.(10)
- начальная фаза входного тока.(10) (11)
(11)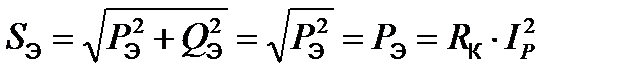 . (12)
. (12) ,
,  ,
, ,
,
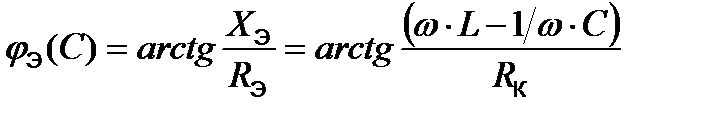 ,
, .
.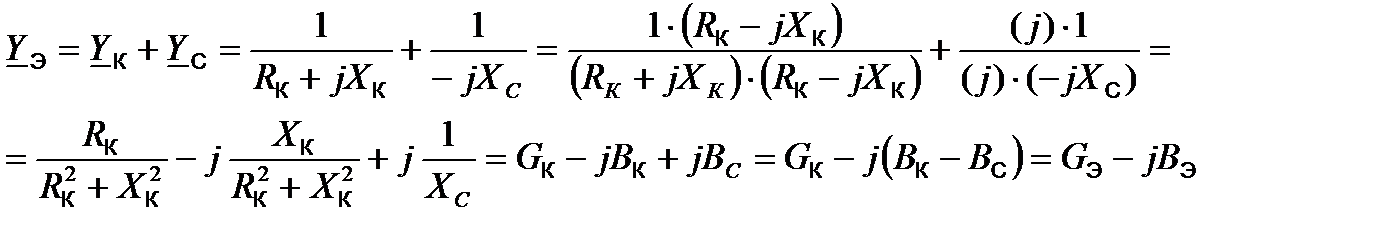 где
где  - соответственно активная и реактивные проводимости катушки и конденсатора. (13)
- соответственно активная и реактивные проводимости катушки и конденсатора. (13)
 или
или  (14)
(14) (15)
(15) (16)
(16) (17)
(17) - чисто активная.(20)
- чисто активная.(20)

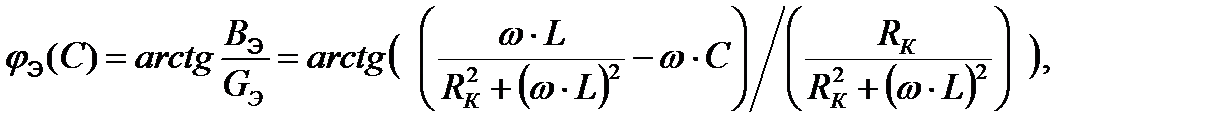
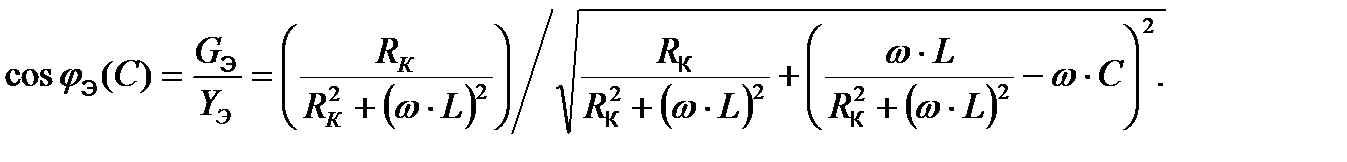
 (21)
(21) , (22)
, (22) , а полная компенсация требует дополнительной установки значительной емкости (дополнительной батареи конденсаторов), что часто экономически не оправдывается.
, а полная компенсация требует дополнительной установки значительной емкости (дополнительной батареи конденсаторов), что часто экономически не оправдывается. (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27)