 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аналіз моделей на чутливістьСтр 1 из 2Следующая ⇒
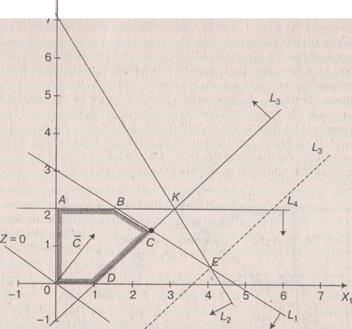
Аналіз моделей на чутливість - це процес, який реалізується після отримання оптимального рішення. В рамках такого аналізу виявляється чутливість оптимального рішення до визначених змін вихідної моделі. У задачі про асортимент продукції може виникнути питання про те, як вплине на оптимальне рішення збільшення і зменшення попиту на продукцію або запасів вихідної сировини. Можливо, також буде потрібно аналіз впливу ринкових цін на оптимальне рішення. При такому аналізі завжди розглядається комплекс лінійних оптимізаційних моделей. Це додає моделі певну динамічність, дозволяючи досліднику проаналізувати вплив можливих змін вихідних умов на отримане раніше оптимальне рішення. Динамічні характеристики моделей фактично відображають аналогічні характеристики, властиві реальним процесам. Відсутність методів, що дозволяють виявляти вплив можливих змін параметрів моделі на оптимальне рішення, може привести до того, що отримане (статичне) рішення застаріє ще до своєї реалізації. Для проведення аналізу моделі на чутливість з успіхом можуть бути використані графічні методи . Розглянемо основні завдання аналізу на чутливістьна прикладі 7.10 Задача 1 . Аналіз змін запасів ресурсів. Після знаходження оптимального рішення потрібно з'ясувати, як відіб'ється на оптимальному рішенні зміна запасів ресурсів. Для цього необхідно відповісти на два питання: 1. На скільки можна збільшити запас деякого ресурсу для поліпшення отриманого оптимального значення цільової функції Z? 2. На скільки можна знизити запас деякого ресурсу при зберіганні отриманого оптимального значення цільової функції Z? Перш ніж відповісти на поставлені питання, класифікуємо обмеження лінійної моделі як зв’язані (активні) та незв’язані (неактивні) обмеження. Пряма, що представляє зв'язані обмеження, повинна проходити через оптимальну точку, в іншому випадку, відповідне обмеження буде незв’язаним. На рис. 7.5 зв'язаним обмеженнями є обмеження (1) і (3), представлені прямими L1 і L2 відповідно, тобто ті, які визначають запаси вихідних ресурсів. Обмеження (1) визначає запаси сировини А. Обмеження (3) визначає співвідношення попиту на продукцію, що випускається. Якщо деяке обмеження є зв'язаним, то відповідний ресурс відносять до розряду дефіцитних ресурсів, так як він використовується повністю. Ресурс, з яким асоційовано незв’язані обмеження, слід віднести до розряду недефіцитних ресурсів (тобто наявних у деякому надлишку). У нашому прикладі незв’язаними обмеженнями є (2) і (4). Відповідно, ресурс − сировина В − недефіцитний, тобто існує надлишок даного ресурсу, а попит на продукцію П2 не буде задоволено повністю (у таблиці - ресурси 2 і 4). При аналізі моделі на чутливість до правих частин обмежень визначаються: 1) гранично допустиме збільшення запасу дефіцитного ресурсу, що дозволяє поліпшити знайдене оптимальне рішення, і 2) гранично допустиме зниження запасу недефіцитних ресурсу, не змінює знайдене раніше оптимальне значення цільової функції. У нашому прикладі сировина А і співвідношення попиту на продукцію, що випускається П1і П2 є дефіцитними ресурсами (у таблиці - ресурси 1,3). Розглянемо спочатку ресурс - сировина А. На рис. 7.7 при збільшенні запасу цього ресурсу пряма L1 переміщується вгору, паралельно самій собі, до точки К, в якій перетинаються лінії обмежень L2, L3 і L4. У точці К обмеження (2), (3) і (4) стають зв'язаними; оптимальному рішенню при цьому відповідає точка К, а простором (допустимих) рішень стає багатокутник АКДО. У точці К обмеження (1) (для ресурсу А) стає надлишковим, оскільки будь-який подальший ріст запасу відповідного ресурсу не впливає ні на простір рішень, ні на оптимальне рішення. Таким чином, обсяг ресурсу А не варто збільшувати понад тієї межі, коли відповідне йому обмеження (1) стає надлишковим, тобто пряма (1) проходить через нову оптимальну точку К. Цей граничний рівень визначається наступним чином. Встановлюються координати точки К, в якій перетинаються прямі L2, L3 і L4, тобто знаходимо рішення системи рівнянь
Рис. 7.7. Геометрична інтерпретація рішення задачі лінійного програмування (зміна ресурсу А) В результаті отримаємо х1 = 3 і х2 = 2. Потім, шляхом підстановки координат точки К в ліву частину обмеження (1), визначається максимально допустимий запас ресурсу А. 2х1+ 3х2 = 2*3 + 3 *2 = 12. . Рис. 7.8 ілюструє ситуацію, коли розглядається питання про зміну співвідношення попиту на продукцію П1 і П2
Рис. 7.8. Геометрична інтерпретація рішення задачі лінійного програмування (зміна попиту на продукцію) Нової оптимальної точкою стає точка Е, де перетинаються прямі L1і L2 . Координати цієї точки знаходяться шляхом рішення системи рівнянь (1) і (2) наступним чином:
В результаті виходить х1=4,2; х2=0,2, причому добовий попит на продукцію П1 не повинен перевищувати попит на продукцію П2 на величину х1+х2= 4,2 - 0,2 = 4 од. Подальше збільшення розриву в попиті на продукцію П1 і П2 не впливатиме на оптимальне рішення. Розглянемо питання про зменшення правої частини незв’язаних обмежень. Обмеження (4) Розглянемо обмеження (2)
Результати проведеного аналізу можна звести в наступну таблицю:
Задача 2. Визначення найбільш вигідного ресурсу. У задачі 1 аналізу на чутливість ми досліджували впливав на оптимум збільшення обсягу дефіцитних ресурсів. При обмеженнях, пов'язаних з додатковим залученням ресурсів, природно поставити питання: якому з ресурсів слід віддати перевагу при вкладенні додаткових коштів? Для цього вводиться характеристика цінності кожної додаткової одиниці дефіцитного ресурсу, що виражається через відповідне збільшення оптимального значення цільової функції. Таку характеристику для розглянутого прикладу можна отримати не посередньо з таблиці, в якій наведено результати вирішення завдання 1 на чутливість. Позначимо цінність додаткової одиниці ресурсу і через уі. Величина уі визначається із співвідношення уі = Результати розрахунку цінності одиниці кожного з ресурсів представлені в наступній таблиці:
Отримані результати свідчать про те, що додатково тільні вкладення в першу чергу слід направити на збільшення ресурсу А і лише потім − на формування співвідношення попиту на продукцію П1 і продукцію П2. Що стосується недефіцитних ресурсів, то, як і слід було очікувати, їх обсяг збільшувати не слід. Завдання 3. Визначення меж зміни коефіцієнтів цільової функції. Зміна коефіцієнтів цільової функції впливає на нахил прямої, яка представляє цю функцію в даній системі координат. Варіація коефіцієнтів цільової функції може привести до зміни сукупності зв'язаних обмежень і, відповідно, статусу того чи іншого ресурсу (тобто зробити недефіцитний ресурс дефіцитним, і навпаки). При аналізі моделі на чутливість до змін коефіцієнта цільової функції необхідно дослідити наступні питання: 1. Який діапазон зміни того чи іншого коефіцієнта цільової функції, при якому не відбувається зміни оптимального рішення? 2. На скільки варто змінити той чи інший коефіцієнт цільової функції, щоб зробити певний недефіцитних ресурс дефіцитним, і, навпаки, дефіцитний ресурс зробити недефіцитним? Відповімо на ці запитання на нашому прикладі. Розглядаючи перше питання, позначимо через с1, і с2 доходи підприємства від продажу одиниці продукції П 1 і П2 відповідно. Тоді цільову функцію можна представити в наступному вигляді: Z=c1x1+c2x2. На рис. 7.5 видно, що при збільшенні с1 або зменшенні с2 пряма, що представляє цільову функцію Z, обертається (навколо точки С) за годинниковою стрілкою. Якщо ж с1 зменшується або с2 збільшується то пряма обертається в протилежному напрямку – проти годинникової стрілки. Таким чином, точка С буде залишатися оптимальною точкою доти, поки нахил прямої не вийде за межі, обумовлені нахилами прямих для обмежень (1)і (3). Коли нахил прямої Z стане рівним нахилу прямої L1,отримуємо дві альтернативні оптимальні кутові точки - С і В. Аналогічно, якщо нахил прямої Z стане рівним нахилу прямої для обмеження (3), будемо мати альтернативні оптимальні кутові точки С і D . Наявність альтернативних оптимумів свідчить про те, що одне і те ж оптимальне значення Z може досягатися при різних значеннях змінних х1 і х2. Як тільки нахил прямої вийде за межі вказаного вище інтервалу с1, одержимо деяке нове оптимальне рішення. Розглянемо на нашому прикладі, яким чином можна знайти допустимий інтервал зміни с1, при якому точка С залишається оптимальною. Початкове значення коефіцієнта с2 = 4 залишимо незміненими. На рис. 7.5 видно, що значення с1, можна зменшувати до тих пір, поки пряма Z не співпаде з прямою L1 (відрізок ВС). Це крайнє мінімальне значення коефіцієнта с1, можна визначити з рівності кутів нахилів прямої Z і прямої L1. Так як тангенс кута нахилу для прямої Z рівний Інтервал зміни с1, в якому точка С як і раніше залишається єдиною оптимальною точкою, визначається нерівністю Можна помітити, що, як тільки коефіцієнт с1 виявляється менше
Поиск по сайту: |


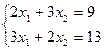
 фіксує граничний рівень попиту на продукцію П2. З рис. 7.5 випливає, що, не змінюючи оптимального рішення, пряму L4 (АВ) можна опускати вниз до перетину з оптимальною точкою С. Оскільки точка С має координати х1=2,4; х2=1,4, зменшення попиту на продукцію П2 до величини х2=1,4 ніяк не вплине на оптимальність раніше отриманого рішення.
фіксує граничний рівень попиту на продукцію П2. З рис. 7.5 випливає, що, не змінюючи оптимального рішення, пряму L4 (АВ) можна опускати вниз до перетину з оптимальною точкою С. Оскільки точка С має координати х1=2,4; х2=1,4, зменшення попиту на продукцію П2 до величини х2=1,4 ніяк не вплине на оптимальність раніше отриманого рішення. , яке являє собою обмеження на недефіцитний ресурс - сировину В. І в цьому випадку праву частину - запаси сировини В - можна зменшувати до тих пір, поки пряма L2 не досягне точки С. При цьому права частина обмеження (2) стане рівною 3х1+2х2=3*2,4+2*1,4=10,0, що дозволяє записати це обмеження у вигляді:
, яке являє собою обмеження на недефіцитний ресурс - сировину В. І в цьому випадку праву частину - запаси сировини В - можна зменшувати до тих пір, поки пряма L2 не досягне точки С. При цьому права частина обмеження (2) стане рівною 3х1+2х2=3*2,4+2*1,4=10,0, що дозволяє записати це обмеження у вигляді:  . Цей результат показує, що раніше отримане оптимальне рішення не зміниться, якщо добовий запас ресурсу В зменшити на 3 од.
. Цей результат показує, що раніше отримане оптимальне рішення не зміниться, якщо добовий запас ресурсу В зменшити на 3 од. .
.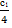 , а для прямої (1) дорівнює 2/3, то мінімальне значення с1, визначимо з рівності
, а для прямої (1) дорівнює 2/3, то мінімальне значення с1, визначимо з рівності  =
=  , звідси min с1=
, звідси min с1=  . На рис. 7,5 видно, щ значення с1 можна збільшувати необмежено, так як пряма Z при с2=4 і с1
. На рис. 7,5 видно, щ значення с1 можна збільшувати необмежено, так як пряма Z при с2=4 і с1  +∞ не співпадають з прямою L3 (DC) і точка С при всіх значеннях коефіцієнта с1
+∞ не співпадають з прямою L3 (DC) і точка С при всіх значеннях коефіцієнта с1 
 . При с1=
. При с1=  , ресурс 3 стає недефіцитним, а ресурс 4 – дефіцитний. Для підприємства це означає наступне: якщо дохід від продажу одиниці продукції П1, стане менше
, ресурс 3 стає недефіцитним, а ресурс 4 – дефіцитний. Для підприємства це означає наступне: якщо дохід від продажу одиниці продукції П1, стане менше  д. е., то найбільш вигідна виробнича програма підприємства повинна передбачати випуск максимально допустимої кількості продукції П2 (повністю задовольняти попит на продукцію П2). При цьому співвідношення попиту на продукцію П1, і П2 не буде лімітувати обсяги виробництва, що обумовить не дефіцитність ресурсу (3). Збільшення коефіцієнта с1, понад
д. е., то найбільш вигідна виробнича програма підприємства повинна передбачати випуск максимально допустимої кількості продукції П2 (повністю задовольняти попит на продукцію П2). При цьому співвідношення попиту на продукцію П1, і П2 не буде лімітувати обсяги виробництва, що обумовить не дефіцитність ресурсу (3). Збільшення коефіцієнта с1, понад