 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ряды распределения: определение, элементы, виды. Построение рядов распределения
Ряд распределения(РР)- результат первичной группировки собранных статистических данных, под которым понимают группировку наблюдений за значениями одного и того же показателя в один и тот же момент времени по разным единицам совокупности. РР всегда состоит из 2 частей: значений вариант и соответствующих им частот (частостей). Варианта-значение, которое может принимать признак в рр. Частота-кол-во ед.наблюдения, обладающих значением данной варианты. Частости-это частоты, выраженные либо в долях единиц, либо в % к объему совокупности). Виды: атрибутивные(по качественному признаку) и вариационные (по количественному признаку). Вариационные бывают дискретные (значение принака выраж.конкретным числом), и интервальными (знач.показателя задаются в виде интервалов). Построение дискрет.вариац.ряда: записать в порядке возрастания значения которые принимает признак(варианты) и подсчитать сколько раз встречается каждый вариант(частоту).Результаты оформить в табл. Интервальный ряд с рвными интервалами: 1)число интервалов 2)Определение велечины интервалов 3)Определение границ интервалов 4) подсчитать частоты. Виды статистических таблиц. В зависимости от характера разработки подлежащего различают простые (характеризуют динамику каких либо показателей), групповые и комбинационные статистические таблицы.Груп. и комбинац. Таблицы характеризуют структуру социально-экономических явлений,показывают их взаимосвязь. Групповая содержит группировку по одному атрибутивному или количественному признаку. Комбинац.табл- комбинация двух и более прищнаков, которые легли в основу группировки. 9.Абсолютные величины. Характеризуют абсолютные размеры соц.-экономич. Явлений,их признаков в натуральных единицах измерения, в денежных или трудовых(чел-дни и тд). Различают индивидуальные, групповые и общие. Относительные величины, их виды. (примеры) Мера количественного соотношения статистических показателей.Отображают относит.размеры соц-экономич явлений. Различают несколько видов: ОВПЗ, ОВВП, ОВД,ОВС,ОВПС, и т.д
11.Виды средних величин. Уметь приводить примеры. Виды средних величин Средние величины делятся на два больших класса: степенные средние и структурные средние Степенные средние: Виды средних величин
Структурные средние: § Мода
§ Медиана
§ Квартили
12.Свойства средней арифметической. Способы ее исчисления. свойство средней арифметической. 1. ¯A= A Среднее от постоянной равно ей самой 2. ¯(А±X)= X±A Увеличение или уменьшение одно и того же величину приводит к изменению средней на ту же величину. 3. ¯АX= A¯X Умножение/деление каждого варианта в А раз изменяет среднюю во столько же раз. (∑X(Af))/(∑Af)= (А∑X f)/(A∑F) 4. Изменение каждого из весов в одно и тоже количество раз не изменяет величины среднего показателя. 5. Алгебраическая сумма отклонений всех вариантов от средней арифметической равно 0 Сумма(Хi-Xcpед)fi=0 6. Среднее от суммы или разности нескольких величин равна сумме средних значений этих величин. 7. Сумма квадратов отклонений от средней арифметической меньше, чем от любой другой величины. Способы ее исчисления Средняя арифметическая простая величина определяется по формуле X= (∑Xi)/N=(∑X)/N. Средняя арифметическая взвешенная величина определяется по формуле X= (∑(Xi Fi))/(∑Fi)=(∑XF)/(∑Fi) , Fi – частота повторение признака Xi у различных единиц совокупности. 13.Структурные средние, методика их исчисления в дискретных и интервальных рядах распределения. 1.Мода Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного рядаявляется варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
§ § § § § §
Медиана Медиана —это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот Ме= (n(число признаков в совокупности)+ 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда). При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
2.
квартили
14Абсолютные показатели вариации. Их значение в статистическом анализе. Абсолютные показатели § размах вариации: § среднее линейное отклонение: § среднеквадратическое отклонение: § § дисперсия: Значение: 15.Относительные показатели вариации. Их значение в статистическом анализе.
Поиск по сайту: |










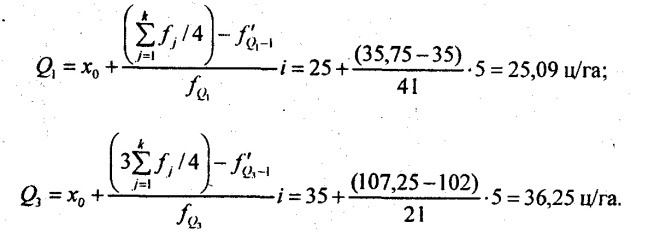 дециль
дециль 
 — значение моды
— значение моды — нижняя граница модального интервала
— нижняя граница модального интервала — величина интервала
— величина интервала — частота модального интервала
— частота модального интервала — частота интервала, предшествующего модальному
— частота интервала, предшествующего модальному — частота интервала, следующего за модальным
— частота интервала, следующего за модальным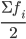 , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле: — искомая медиана
— искомая медиана — сумма частот или число членов ряда
— сумма частот или число членов ряда - сумма накопленных частот интервалов, предшествующих медианному
- сумма накопленных частот интервалов, предшествующих медианному ;
;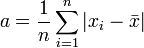 ; (то же самое + вес f)
; (то же самое + вес f) ;(то же самое + вес f)
;(то же самое + вес f) ;(то же самое + вес f)
;(то же самое + вес f)