 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление площади криволинейного сектора ⇐ ПредыдущаяСтр 3 из 3
Доказательство: Пусть мы работаем в полярных координатах и имеем дело с кривой r=r (q ) , a £ q £ b Фигуру , ограниченную : А) графиком кривой r=r (q ) Б) прямыми q = a и q = b назовём криволинейным сектором .
Разобьём отрезок [a , b ] на части точками q1, q 2 , …q n-1 , так ,что a = q 0 <q 1<q 2<…<q n-1<q n-b и обозначим l = max D q I Пусть mi = int r (q ) ? Mi = sup r(0) и q Î [ q I, q I+1] q = [ q I, q I+1]
Так как Если при l ® 0 существует lim s и lim S и они равны друг другу , то их общее значение называется площадью криволинейного сектора . P= lim s = lim S Но так как s и S есть снова суммы Дарбу , то
что и определяет площадь криволинейного сектора .
Длина дуги 1. Длина дуги в прямоугольной системе координат
Пусть кривая L задана уравнением у = у(х),причем у(х) — непрерывно дифференцируемая функция на [а, Ь]. Разобьем ее на п частей точками с абсциссами проведем хорды через эти точки (рис. 18.9, а). Получим вписанную ломаную, причем длина его звена равна где а длина всей ломаной, вписанной в кривую L, равна
2. Длина дуги при параметрическом задании L
3. Длина дуги в полярных координатах
Теорема Ролля. Пусть функция Доказательство. Так как функция Теорема Ролля имеет простой геометрический смысл: если крайние ординаты кривой
Теорема Лагранжа. Если функция Формулу (8.7) называют формулой Лагранжа или формулой конечных приращений. Доказательство. Рассмотрим на сегменте
Проверим, что для функции
Из формулы (8.8) очевидно, что
Из равенства (8.9) вытекает формула Лагранжа (8.7). Подчеркнем, что в формуле (8.7) вовсе не обязательно считать, что Замечание. Мы получили теорему Лагранжа как следствие теоремы Ролля. Заметим вместе с тем, что сама теорема Ролля является частным случаем теоремы Лагранжа (при Записывая формулу Лагранжа для сегмента где
где
21. Достаточное условие существования экстремумов
Поиск по сайту: |




 есть площадь кругового сектора радиуса r и углом D q , то s и S есть площадь всех круговых секторов , вписанных и описанных вокруг нашего криволинейного сектора .
есть площадь кругового сектора радиуса r и углом D q , то s и S есть площадь всех круговых секторов , вписанных и описанных вокруг нашего криволинейного сектора .


 По теореме Лагранжа
По теореме Лагранжа 
 .Из определения длины дуги имеем
.Из определения длины дуги имеем  . Так как правая часть есть интегральная сумма для функции
. Так как правая часть есть интегральная сумма для функции  то
то 




 непрерывна на сегменте
непрерывна на сегменте  и дифференцируема во всех внутренних точках этого сегмента. Пусть, кроме того,
и дифференцируема во всех внутренних точках этого сегмента. Пусть, кроме того,  . Тогда внутри сегмента
. Тогда внутри сегмента  такая, что значение производной в этой точке
такая, что значение производной в этой точке  равно нулю. Кратко можно сказать, что между двумя равными значениями дифференцируемой функции обязательно лежит нуль производной этой функции.
равно нулю. Кратко можно сказать, что между двумя равными значениями дифференцируемой функции обязательно лежит нуль производной этой функции. равна нулю в любой точке сегмента
равна нулю в любой точке сегмента  , можно утверждать, что хотя бы одно из двух значений М или m достигается функцией в некоторой внутренней точке
, можно утверждать, что хотя бы одно из двух значений М или m достигается функцией в некоторой внутренней точке  имеет в этой точке
имеет в этой точке 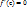 »
» 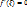 .
.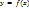 равны, то, согласно теореме Ролля, на кривой
равны, то, согласно теореме Ролля, на кривой 
 найдется точка
найдется точка  (8.7)
(8.7) (8.8)
(8.8) выполнены все условия теоремы Ролля. В самом деле,
выполнены все условия теоремы Ролля. В самом деле, 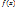 и линейной функции) и во всех внутренних точках сегмента
и линейной функции) и во всех внутренних точках сегмента 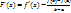
 .Согласно теореме Ролля внутри сегмента
.Согласно теореме Ролля внутри сегмента  (8.9)
(8.9) .
. , будем иметь
, будем иметь  (8.10)
(8.10) . Можно утверждать, что найдется такое (зависящее от
. Можно утверждать, что найдется такое (зависящее от  ) число
) число  из интервала
из интервала  , что
, что 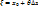 . Таким образом, формуле (8.10) можно придать вид
. Таким образом, формуле (8.10) можно придать вид (8.11)
(8.11) аргумента. Этот вид формулы Лагранжа оправдывает термин «формула конечных приращений».
аргумента. Этот вид формулы Лагранжа оправдывает термин «формула конечных приращений».