 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формула Эйлера и показательная форма комплексного числа ⇐ ПредыдущаяСтр 2 из 2
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой: ejφ = cos φ + j∙sin φ, которая называется формулой Эйлера. Пусть комплексное число z в тригонометрической форме имеет вид z =|z|(cos φ + j∙sin φ). На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим z =|z| ejφ. Эта запись называется показательной формой комплексного числа, |x| - модуль числа; φ – аргумент числа. Примеры: 1) записать число z = -1 + j в показательной форме:
2) записать число z = -1 в показательной форме:
z = ejπ - показательная форма числа. Сложение и вычитание комплексных чисел Суммой двух комплексных чисел z1 = x1 + jy1 и z2 = x2 + jy2 называется число: z1 + z2 = (x1 + x2)+ j(y1 + y2). Операция сложения обладает следующими очевидными свойствами: z1 + z2 = z2 + z1, (z1 + z2)+ z3 = z1 + (z2 + z3). Аналогично определяется вычитание: z1 - z2 = (x1 - x2) + j(y1 - y2). Сложение и вычитание комплексных чисел удобно выполнять, когда они записаны в алгебраической форме. Умножение и деление комплексных чисел Произведением двух комплексных чисел z1 = x1 + jy1 и z2 = x2 + jy2 называется число z1z2 = (x1x2 – у1у2) + j(х1y2 + х2y1). Это определение следует из правила раскрытия скобок, учитывая, что j2 = -1. Пример: (2 - 3j)(-5 + 4j) = -10 + 8j + 15j – 12j2 = -10 + 23j + 12 = 2 + 23j. Операция умножения обладает следующими свойствами: z1z2 = z2z1, (z1z2)z3 = z1(z2z3), z1(z2 + z3) = z1z2 + z1z3. Умножение комплексных чисел удобнее производить, когда они записаны в тригонометрической или показательной форме. Так, если есть два числа z1 = |z1|(cos φ1 + j∙sin φ1) иz2 = |z2|(cos φ2 + j∙sin φ2),то z1 z2= |z1||z2|(cos (φ1 + φ2)+ j∙sin( φ1 + φ2)). Аналогично Т.е. при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило действует и при возведении комплексного числа в степень
Эта формула называется формулой Муавра. Пример: вычислить Для начала запишем число
По формуле Муавра:
Частное от деления двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 определяется по формуле
При делении комплексных чисел, записанных в алгебраической форме, необходимо домножать числитель и знаменательна сопряженное знаменателю, чтобы избавиться от мнимой части в знаменателе, например:
Как и умножение, деление комплексных чисел удобнее производить, когда числа записаны в тригонометрической или показательной форме
Поиск по сайту: |
 ,
, 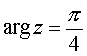 ,
, - показательная форма числа;
- показательная форма числа;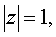
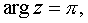
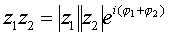

 .
. в тригонометрической форме, для этого вычислим его модуль и аргумент:
в тригонометрической форме, для этого вычислим его модуль и аргумент:


 .
.


