 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Переходные процессы в цепи с ёмкостью ⇐ ПредыдущаяСтр 4 из 4
Предположим, что t=0⇒ qC=0, UC=0. Замыкаем ключ i=(ε-UC)/R, UC=qC/C. iR=ε-(qC/C)⇒(di/dt)R=-(1/C)i. (dq/dt=1). di/i=-(1/RC)dt . i=I0 I0=ε/R. τ=RC. UC=ε-iR= ε(1- Процесс разрядки конденсатора: t=0след.UC= ε. iR=-UC=-qC/C. R(di/dt)=-i/C. i=I0 e^(-t/τ). I0=-ε/R. τ=RC. UC=iR=ε e^(-t/τ). График1 –интегрирование по отношению напряжения относительно конденсатора. Мгновенно изменить напряжение емкости не возможно. График2 – дифференциальный по отношению к силе тока относительно конденсатора.
Переходные процессы в цепи с индуктивностью. t=0⇒i=0. После замыкания ключа i=(ε+εс)/R= (ε-L(di/dt))/R. iR= ε- L(di/dt). iR+UL= L(di/dt). UL= ε- iR. (d UL/dt)=-R(di/dt). UL= U0 e^(-t/τ). U0= ε, τ=L/R. i=I0(1-e^(-t/τ)) где I0= ε/R ,τ=L/R. t=0⇒i=I0. i= ε/R=-L di/dt. i=I0 e^(-t/τ). UL=-iR=- εe^(-t/τ). 2 закона коммутации :мгновенно изменить силу тока в цепи с индуктивностью не может. Мгновенно изменить силу тока в цепи с индуктивностью невозможно. R,L,C,ε – не зависят от силы тока и поэтому цепь нелинейная.
Свободные незатухающие электромагнитные колебания. Т-это наименьший промежуток времени между двумя одинаковыми расстояниями. Т=[с], ν=1/T, ν=[Гц]. ω=2πν –циклическая частота ω=рад/с. Вынужденные колебания возникают под действием силы. U(C)=U(0) исходное состояние то i=0
Если применить потери энергии, то токи колебания затухающие: C I=
Свободные затухающие электромагнитные колебания.
1) D<0след.β<2, 2)D>0, β> β>0 нет колебания..
Вынужденные гармонические колебания. u= 1)схема u= 2)схема u= 3)схема i=
Волновое движение. Волновой процесс —распространение колебаний в сплошной среде. Сплошная среда — непрерывно распределенная в пространстве и обладающая упругими свойствами. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояния колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества. Герц получал электромагнитные волны, возбуждая в вибраторе с помощью источника высокого напряжения серию импульсов быстропеременного тока. Колебания электрических зарядов в вибраторе создают электромагнитную волну. Только колебания в вибраторе совершает не одна заряженная частица, а огромное количество электронов, движущихся согласованно. Электромагнитные волны регистрировались приёмным вибратором, представляющего собой точно такое же устройство, что и излучающий вибратор. Под действием переменного электрического поля электромагнитной волны в приемном вибраторе возбуждаются колебания тока. Если собственная частота приемного вибратора совпадет с частотой электромагнитной волны, наблюдается резонанс и колебания в приемном вибраторе происходят с большой амплитудой. Герц обнаруживал их, наблюдая искорки в очень малом промежутке между проводниками приемного вибратора.
Ур-е Максвела.
Система ур-й Максвела: а) полевые ур-я М.: 1)интегральная форма, 2) диф. форма. Теорема Гаусса включающая з-н Кулона, его полевую трактовку эл. тока:1) Теорема Гаусса для магнитного поля: 1) З-н электромагнитной индукции: 1) 2) Теорема о Циркуляции:1) б) Материальные ур-я М.:
Поиск по сайту: |
 . I0-это i в момент времени t=0.
. I0-это i в момент времени t=0. =C
=C 
 =0.
=0.  =0, i=
=0, i=  ,
,  =L
=L  /2.
/2. , i=0,
, i=0,  /2,
/2,  /2.
/2. /2)+(I
/2)+(I  /2).
/2).  ,
,  /C=-L(di/dt), (
/C=-L(di/dt), (  i/d
i/d  )+(i/LC)=0,
)+(i/LC)=0,  =1/LC, (
=1/LC, (  t+C), i=I_0sinω_0t. ɥ=0, C
t+C), i=I_0sinω_0t. ɥ=0, C  ,
,  , T=2π
, T=2π  формула Томсона.
формула Томсона. +2βk+
+2βk+  -
-  =-β±
=-β±  . i=
. i=  sinωt.
sinωt.  =
=  +
+  -------------апериодический разряд конденсатора.
-------------апериодический разряд конденсатора. )
) ωt P=1/T
ωt P=1/T  =
=  /2 P=(
/2 P=(  )*(
)*(  эффект. знач. напряж. на эффект. знач. силы тока. [P]=[Вт]
эффект. знач. напряж. на эффект. знач. силы тока. [P]=[Вт] sin(ωt+
sin(ωt+  ), i=
), i=  =
=  реактивное сопротивление. p=Ui=
реактивное сопротивление. p=Ui=  sin2
sin2  t, P=
t, P=  =0
=0 т.к. Rстремится0, то U+
т.к. Rстремится0, то U+  cosωt, i=
cosωt, i=  =ωLреактивное сопротивление индуктивности, p=Ui=-
=ωLреактивное сопротивление индуктивности, p=Ui=-  =0.
=0. ;
;  - волновое уравнение. Рассмотрим линейную среду:
- волновое уравнение. Рассмотрим линейную среду:  Рассмотрим два ур-я Максвелла: rotẼ=-
Рассмотрим два ур-я Максвелла: rotẼ=-  , rot
, rot  ,
,  , rot
, rot  ,
,  ,
,  ,
,  ;
;  n-показатель преломления среды, V-скорость распространения волны. Герц использовал простое устройство, называемое вибратором Герца. Это устройство представляет собой открытый колебательный контур.
n-показатель преломления среды, V-скорость распространения волны. Герц использовал простое устройство, называемое вибратором Герца. Это устройство представляет собой открытый колебательный контур.

 ;
;  з-н сохр. эл. Заряда;
з-н сохр. эл. Заряда; 

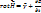 ;
;  - плотность тока смещения;
- плотность тока смещения;  – полный ток.
– полный ток. ; 2)
; 2) 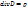 .
. ; 2)
; 2) 
 создаёт вихревое поле.
создаёт вихревое поле. ; 2)
; 2)  – з-н Ома в диф. форме;
– з-н Ома в диф. форме;  ;
;  З-н сохр. эл. Заряда входит в эти ур-я в неявном виде.
З-н сохр. эл. Заряда входит в эти ур-я в неявном виде.