 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Над сходящимися рядами можно выполнять арифметические действия: сложение, вычитание, умножение, деление. Они выполняются как действия над многочленамиСтр 1 из 5Следующая ⇒
ТЕОРИЯ РЯДОВ ЧИСЛОВЫЕ РЯДЫ Основные понятия
Определение. Рядом называется выражение вида Члены ряда образуют бесконечную последовательность. Члены ряда могут обозначать числа, функции, векторы, матрицы и т.п. Очень часто ряд записывается в сокращенной форме:
Многоточие в конце записи указывает на то, что в выражении (1) нет последнего слагаемого. Таким образом, ряд есть «бесконечная» сумма. Определение. Ряд, все члены которого являются числами, называется числовым.
Примеры числовых рядов: а) б) Ряд считается заданным, если известен его общий член Пример. Ряд с общим членом Более сложной является задача: по нескольким первым членам ряда составить общий член ряда. Пример. Найти общий член ряда: Решение. Заметим закономерности для числителей и знаменателей дробей. Числа 2, 4, 6, … отличаются друг от друга на величину Получим В результате для ряда Сумма конечного числа Определение.Ряд называется сходящимся, если последовательность его частичных сумм
Этот предел называетсясуммой сходящегося ряда. Если предел не существует или бесконечен, то ряд называется расходящимся. Ряд, составленный из членов геометрической прогрессии со значениями Геометрический ряд сходится при величине Свойства сходящихся рядов 1. Если ряд 2. Если ряды
и ряд также сходятся, а их сумма и разность равна соответственно Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов. 4. Если ряд Определение.Ряд 5. Если ряд (1) сходится, то Над сходящимися рядами можно выполнять арифметические действия: сложение, вычитание, умножение, деление. Они выполняются как действия над многочленами.
2. Необходимый признак сходимости ряда(теорема). Если ряд
Замечание. Это условие является необходимым, но не достаточным признаком сходимости, то есть из стремления общего члена ряда к нулю не обязательно следует сходимость ряда. Гармонический ряд
Поиск по сайту: |

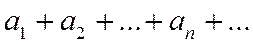 , где числа
, где числа  называются членами ряда. Величина
называются членами ряда. Величина  – общий или
– общий или  -й член ряда.
-й член ряда.
 ,
, .
.
 , т. е. задана функция
, т. е. задана функция  натурального аргумента.
натурального аргумента. имеет вид
имеет вид  .
. .
. , т. е. эти числа образуют арифметическую прогрессию с
, т. е. эти числа образуют арифметическую прогрессию с 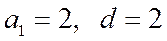 . Тогда величину
. Тогда величину  определим как общий член арифметической прогрессии
определим как общий член арифметической прогрессии 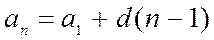 .
. . Аналогично, числа 5, 9, 13, … образуют арифметическую прогрессию со значениями
. Аналогично, числа 5, 9, 13, … образуют арифметическую прогрессию со значениями  . Получим
. Получим  .
. общий член ряда
общий член ряда  .
. первых членов ряда (1)
первых членов ряда (1) 
 называется
называется  -й частичной суммойданного ряда.
-й частичной суммойданного ряда. ,
, 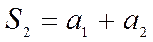 ,
,  , …,
, …,  при неограниченном возрастании
при неограниченном возрастании  имеет конечный предел:
имеет конечный предел: . (2)
. (2) и
и  :
: 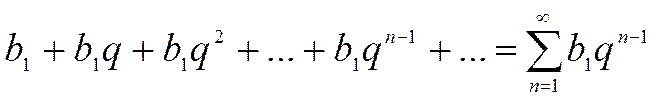 называется геометрическим рядом, где
называется геометрическим рядом, где  .
. и расходится при величине
и расходится при величине  .
. сходится и имеет сумму
сходится и имеет сумму  , то и ряд
, то и ряд  (полученный умножением данного ряда на число
(полученный умножением данного ряда на число  ) также сходится и имеет сумму
) также сходится и имеет сумму  .
. и
и  сходятся и имеют суммы соответственно
сходятся и имеют суммы соответственно  и
и  , то ряды:
, то ряды: (3)
(3) (4)
(4) и
и  .
. сходится, то сходится и ряд
сходится, то сходится и ряд  , полученный отбрасыванием
, полученный отбрасыванием  называется
называется  .
.
 сходится, то его общий член
сходится, то его общий член  при неограниченном увеличении номера
при неограниченном увеличении номера  . (5)
. (5)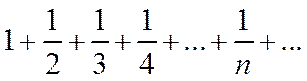 служит примером ряда, у которого предел общего члена
служит примером ряда, у которого предел общего члена  а сам этот ряд расходится
а сам этот ряд расходится