 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИСКОРЕННЯ РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ
Якщо матеріальна точка рухається нерівномірно й непрямолінійно, то її швидкість змінюється як за величиною, так і за напрямком. Ця зміна швидкості у часі характеризується величиною, яка називається прискоренням. Прискоренням руху точки називається фізична величина, що показує на скільки змінюється вектор швидкості матеріальної точки за одиницю часу. При векторному способі завдання руху прискорення руху матеріальної точки дорівнює
Напрямок вектора прискорення,
При координатному способі завдання руху матеріальної точки її координати задаються як функції часу (2). Визначення прискорення точки тут зводиться до знаходження проекції вектора прискорення на координатні осі. При цьому можна знайти модуль вектора прискорення і його орієнтацію, визначивши напрямні косинуси. Згадаємо розкладання вектора швидкості по ортах осей
У цій формулі коефіцієнти при ортах - проекції вектора швидкості на осі координат, які в той же час є першими похідними від координат точки за часом. Знайдемо прискорення точки. Для цього візьмемо першу похідну від векторного рівняння швидкості (11) за часом
де
Формули (19), (20) повністю визначають вектор прискорення. Знайдемо прискорення при природному способі завдання руху матеріальної точки. Для цього скористаємося виразами (15) і (16)
Тут під знаком диференціала знаходиться добуток двох змінних величин, отже:
З формули (21) видно, що вектор прискорення має дві складові. Перша з них (
де R - радіус кривизни траєкторії в даній точці. У векторному виді нормальну складову можна представити так:
При розв’язуванні задач будемо розглядати проекції вектора прискорення на дотичний напрямок і головну нормаль. Проекція вектора прискорення на дотичну Проекція прискорення на головну нормаль Модуль вектора прискорення можна одержати за формулою
Напрямок вектора прискорення визначається тангенсом кута β, утвореного вектором повного й нормального прискорень ( рис. 8).
Поиск по сайту: |
 (16)
(16) збігається з напрямком вектора
збігається з напрямком вектора  . Оскільки положення точки, що рухається, при векторному способі завдання руху визначається її радіус-вектором
. Оскільки положення точки, що рухається, при векторному способі завдання руху визначається її радіус-вектором  , то прискорення точки дорівнює другій похідній від радіус-вектора точки за часом.
, то прискорення точки дорівнює другій похідній від радіус-вектора точки за часом. (17)
(17)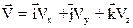
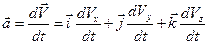 , (18)
, (18) проекції вектора прискорення на координатні осі. Знаючи проекції, можна знайти модуль вектора прискорення і його напрямні косинуси
проекції вектора прискорення на координатні осі. Знаючи проекції, можна знайти модуль вектора прискорення і його напрямні косинуси (19)
(19) (20)
(20)
 (21)
(21) ) спрямована по дотичній до траєкторії, а друга (
) спрямована по дотичній до траєкторії, а друга (  ) збігається з напрямком вектора
) збігається з напрямком вектора  . Можна показати, що вектор
. Можна показати, що вектор  , (22)
, (22) , (23)
, (23) де
де  – одиничний вектор, спрямований уздовж головної нормалі, до центра кривизни траєкторії.
– одиничний вектор, спрямований уздовж головної нормалі, до центра кривизни траєкторії.
 може бути як додатною, так і від’ємною величиною, залежно від напрямку вектора прискорення. Якщо проекція вектора швидкості не змінюється за величиною, то дотичне прискорення дорівнює нулю й рух називається рівномірним. Якщо проекція вектора швидкості збільшується із часом, то дотичне прискорення більше нуля й спрямовано в ту ж сторону, що й швидкість. Рух точки в цьому випадку називається прискореним. Якщо проекція вектора швидкості зменшується з часом, то дотичне прискорення від’ємне й спрямовано убік протилежний напрямку вектора швидкості. Рух точки в цьому випадку називається вповільненим. Дотичне прискорення характеризує зміну швидкості за величиною.
може бути як додатною, так і від’ємною величиною, залежно від напрямку вектора прискорення. Якщо проекція вектора швидкості не змінюється за величиною, то дотичне прискорення дорівнює нулю й рух називається рівномірним. Якщо проекція вектора швидкості збільшується із часом, то дотичне прискорення більше нуля й спрямовано в ту ж сторону, що й швидкість. Рух точки в цьому випадку називається прискореним. Якщо проекція вектора швидкості зменшується з часом, то дотичне прискорення від’ємне й спрямовано убік протилежний напрямку вектора швидкості. Рух точки в цьому випадку називається вповільненим. Дотичне прискорення характеризує зміну швидкості за величиною. завжди додатна величина, тому що чисельник і знаменник додатні. Нормальне прискорення характеризує зміну швидкості за напрямком. Якщо точка рухається по прямій, то радіус кривизни траєкторії дорівнює нескінченності, вектор швидкості не змінюється за напрямком й нормальне прискорення дорівнює нулю.
завжди додатна величина, тому що чисельник і знаменник додатні. Нормальне прискорення характеризує зміну швидкості за напрямком. Якщо точка рухається по прямій, то радіус кривизни траєкторії дорівнює нескінченності, вектор швидкості не змінюється за напрямком й нормальне прискорення дорівнює нулю. (24)
(24)