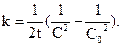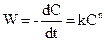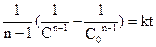|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кінетична класифікація гомогенних хімічних реакцій
З точки зору хімічної кінетики усі елементарні реакції можна класифікувати на реакції нульового, першого, другого та третього порядків. На відміну від молекулярності порядок реакції – величина формальна і дорівнює сумі показників степенів у кінетичному рівнянні. Загальний порядок n даної реакції дорівнює n = nA + nB + nD. При цьому величини nA, nB, nD називаються приватними порядками реакції за речовинами А, В і D. Отже, загальний порядок реакції n дорівнює сумі приватних порядків. Для елементарних реакцій nA = a , nB = b, nD = d. Можливі такі типи кінетичних рівнянь елементарних реакцій:
Реакції нульового порядку – це реакції, які проходять при надлишку реагентів так, що змінювання концентрації не впливає на швидкість реакції. Знайдемо основні кінетичні характеристики і рівняння для гомогенних хімічних реакцій різного порядку у закритих системах при постійності об¢єму та температури. 1. Реакції нульового порядку. Такі реакції трапляються рідко. Прикладом реакції нульового порядку є реакція розкладання N2O5 у газовій фазі за наявності твердого N2O5, коли постійна концентрація реагенту у газовій фазі підтримується сталою за рахунок випарювання твердого оксиду. Для реакцій нульового порядку:
Розв¢яжемо це рівняння, розділивши змінні:
Після інтегрування де В – константа інтегрування. Знайдемо її, ураховуючи початкову умову у момент t = 0 концентрація дорівнює початковій С = С0, звідси С0 = В і С = С0 – k∙t. Отже, у реакціях нульового порядку концентрація лінійно зменшується з часом (рис. 9.2,а). Константу швидкості реакції нульового порядку можна обчислити за рівнянням:
Поряд з константою швидкості для характеристики реакцій часто використовують величину, що називається часом напівперетворення t1/2 .
Рисунок 9.2 – Змінювання концентрації з часом у реакціях нульового (а), першого (б), другого (в) і третього (г) порядків
Час напівперетворення - проміжок часу, за який реагує половина вихідної кількості речовини, тобто при t = t1/2 C = C0/2 звідси:
Отже, для реакції нульового порядку час напівперетворення пропорційний початковій концентрації вихідної речовини. 2. Реакції першого порядку. До елементарних реакцій першого порядку належать реакції, які можна подати у вигляді: А Частіше всього це реакції розкладання. Наприклад, реакція розкладання ацетону: СН3СОСН3 Кінетичне рівняння для реакцій першого порядку має вигляд:
Проінтегруємо його, розділивши змінні:
ln C = - kt + B. Для визначення постійної інтегрування припустимо, що у початковий момент реакції t = 0 концентрація вихідної речовини була С0, тоді ln C0 = B, отже: ln C = - kt + lnC0 або
Це інтегральна форма кінетичного рівняння реакції 1–го порядку. Константа швидкості реакції першого порядку має розмірність (с)-1. Величина, зворотна константі швидкості реакції першого порядку, має розмірність часу і називається середньою тривалістю життя окремої частинки. Для реакції першого порядку характерна лінійна залежність lnC від t (рис. 9.2,б). Знайдемо час напівперетворення для реакції першого порядку. Для t = t1/2 C = C0 /2. Тому:
Бачимо, що час напівперетворення визначається виключно значенням константи швидкості. Так, для наведеної реакції розкладання ацетону k = 4,27 × 10-4 c-1. Отже:
До істинно молекулярних або, краще сказати, моноатомних процесів першого порядку відносять усі численні перетворення радіоактивних речовин. У таблиці наведені деякі дані для таких реакцій. Класичним прикладом реакції першого порядку є реакція інверсії тростинного цукру (сахарози) Таблиця 1.1 – Кінетичні характеристики радіоактивного розпаду деяких ізотопів
С12Н22О11 + Н2О сахароза глюкоза фруктоза
Кінетичне рівняння цієї реакції має вигляд:
У реакції беруть участь ще вода та кислота (іони Н+), однак концентрація кислоти є постійною (іони Н+ - каталізатор), а концентрація води, що міститься у дуже великому надлишку, теж практично постійна. Реакція інверсії зручна для вивчення тим, що у ході її змінюється кут обертання площини поляризації. Сахароза обертає площину поляризації управо, а суміш глюкози та фруктози – уліво. Поміщаючи розчин сахарози у трубку поляриметра, можна стежити за проходженням реакції, не перериваючи її. При кінетичних розрахунках використовується пропорційний зв¢язок між кутом обертання та концентрацією обертальної речовини. 3.Реакції другого порядку. Реакції другого порядку проходять з участю двох частинок (молекул, атомів). Якщо у елементарній реакції беруть участь дві однакові частинки 2А то кінетичне рівняння має вигляд
де С – концентрація речовини А. Інтегрування цього рівняння приводить до:
При t = 0, C = C0. Звідси
Для реакції другого порядку спостерігається лінійна залежність 1/с від t (рис. 10.2, в). Розмірність константи швидкості реакції другого порядку (моль/л)-1×с-1, тобто на відміну від реакцій першого порядку у розмірності є не тільки час, але й концентрація. Тому для реакцій другого порядку ( та вище) не можна при розрахунках замінювати концентрацію на пропорційні неї їй величини. Для реакції другого порядку:
тобто чим більша початкова концентрація, тим менший час напівперетворення. Якщо в елементарній реакції другого порядку реагують дві різні частинки: А1 + А2 причому концентрації речовин А1 та А2 різні, то:
Враховуючи, що С1 = С1п – х та С2 = С2п – х, маємо
де С1п та С2п – початкові концентрації речовин А1 та А2, х – зменшення їх концентрації у момент часу t. Розв¢язок останнього рівняння дає:
Реакцій другого порядку багато. Наприклад: Н2 + І2(пар) 2HI
4 Реакції третього порядку. Елементарні реакції третього порядку можна подати у вигляді: 3А 2A1+ A2 A1 + A2 + A3 Оскільки реакції третього порядку спостерігаються дуже рідко та не становлять значного практичного інтересу, розглянемо їх кінетику тільки для випадку рівності концентрацій усіх реагуючих речовин. Тоді
Та після інтегрування
При t = 0 C = C0 та
Концентрація швидкості реакції третього порядку має розмірність (моль/л)-2×с-1. Для реакцій третього порядку лінійна залежність 1/С2 = f(t) (рис. 10.2, г). Час напівперетворення для реакцій третього порядку обернено пропорційний квадрату концентрації:
Прикладами реакцій третього порядку є: 2NO + O2 2NO + Cl2
Слід зазначити, що реакції першого, другого та третього порядків є у той самий час моно-, бі- та тримолекулярними відповідно. Для моделювання хіміко-технологічних процесів корисно ввести поняття формально простих реакцій. До формально простих реакцій відносять будь-які реакції, для яких кінетичне рівняння може бути подане наближено у вигляді степеневої залежності W = kC1n(1) × C2n(2) × C3n(3) … Наприклад, такою є складна реакція 3СН3ОН + 2Н2CrO4 + 6HCl Для цієї реакції: W = kC(CH3OH) × C(H2CrO4) × C2(HCl). Як бачимо, степенів для формально простої реакції не збігаються зі стехіометричними коефіцієнтами. У загальному випадку для таких реакцій показники степенів можуть бути дробовими і набувати значень, більших від трьох. При рівності концентрацій реагуючих речовин кінетичне рівняння має вигляд
Розв¢язання цього рівняння аналогічне попереднім і приводить до таких результатів:
Константа швидкості має розмірність (моль/л)-(n-1) × с-1.
Поиск по сайту: |
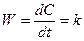

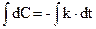 отримаємо: С = - k∙t + B,
отримаємо: С = - k∙t + B,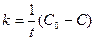 .Її розмірність (моль/л×с-1).
.Її розмірність (моль/л×с-1).
 і
і 
 продукти.
продукти.
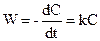 .
.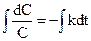
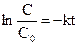 ,
, 
 ;
; 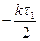 = ln 2; Звідси:
= ln 2; Звідси: 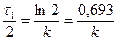

 C6H12O6 + C6H12O6.
C6H12O6 + C6H12O6.
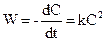
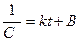
 отже:
отже: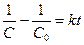 або
або 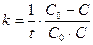
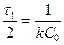
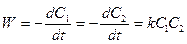
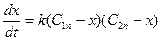
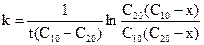 .
. 2HI,
2HI,
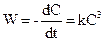

 . Отже:
. Отже: , або
, або