 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Механические колебания: груз на пружине, математический и физический маятники
1). Пружинный маятник – груз массой m, подвешенный на абсолютно упругой невесомой пружине (рис. 5.3). В положении равновесия сила тяжести
или где Если дополнительно сместить груз от положения равновесия на расстояние x, то результирующая сил В проекции на ось Х: второй закон Ньютона иметь вид
но по закону Гука: получим Разделим это уравнение на m и введем обозначение
Его решением является функция: Следовательно, груз, подвешенный на пружине будет совершать гармонические колебания с циклической частотой Известно, что
2). Физический маятник - твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через центр масс тела.(рис.5.4) Если маятник отклонить от положения равновесия на угол
При малых углах
где J –момент инерции маятника относительно оси колебаний, а – расстояние от оси колебаний до центра масс маятника (см. рис.5.4). Введя обозначение
аналогичное уравнению (5.2.3), решение которого известно:
Следовательно, при малых углах отклонения физический маятник совершает гармонические колебания с периодом
или
3) Математический маятник – материальная точка массой m, подвешенная на нерастяжимой невесомой нити длиной
Тогда, дифференциальное уравнение колебаний примет вид:
и его решение: Здесь Период его колебаний равен :
Поиск по сайту: |
 уравновешивается силой упругости
уравновешивается силой упругости 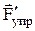 :
:
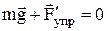
 , (5.2.1)
, (5.2.1) - статическое удлинение пружины при подвешивании груза, k – коэффициент жесткости пружины.
- статическое удлинение пружины при подвешивании груза, k – коэффициент жесткости пружины. и силы тяжести уже не будет равна нулю.
и силы тяжести уже не будет равна нулю. ,
, , где х – смещение груза от положения равновесия. Учитывая, что согласно (5.2.1)
, где х – смещение груза от положения равновесия. Учитывая, что согласно (5.2.1)  , а ускорение
, а ускорение 
 . (5.2.2)
. (5.2.2)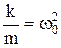 . Перенесем все слагаемые в левую часть и получим дифференциальное уравнение движения пружинного маятника:
. Перенесем все слагаемые в левую часть и получим дифференциальное уравнение движения пружинного маятника: . (5.2.3)
. (5.2.3) .
. .
. , Тогда имеем :
, Тогда имеем :  - период колебания пружинного маятника.
- период колебания пружинного маятника. , то сила тяжести
, то сила тяжести 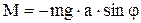 . Тогда в соответствии с уравнением динамики вращательного движения можно записать:
. Тогда в соответствии с уравнением динамики вращательного движения можно записать:
 , где угловое ускорение
, где угловое ускорение  . Тогда:
. Тогда: (5.2.4)
(5.2.4)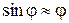 , следовательно, уравнение (5.2.4) примет вид:
, следовательно, уравнение (5.2.4) примет вид: , (5.2.5)
, (5.2.5) , получим уравнение
, получим уравнение , (5.2.6)
, (5.2.6)
 . (5.2.7)
. (5.2.7) , где
, где  - приведенная длина физического маятника
- приведенная длина физического маятника .(рис.5.5)
.(рис.5.5) Математический маятник можно рассматривать как частный случай физического маятника. Момент инерции математического маятника
Математический маятник можно рассматривать как частный случай физического маятника. Момент инерции математического маятника  , где
, где 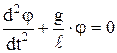 (5.2.8)
(5.2.8) .
. , где g- ускорение свободного падения,
, где g- ускорение свободного падения, 