 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обчислення потрійного інтеграла ⇐ ПредыдущаяСтр 2 из 2
Означення. Якщо будь-яка пряма, яка проходить через внутрішню точку області
Нехай область Припустимо, що кожна пряма, яка паралельна осі
Тобто, щоб обчислити потрійний інтеграл, спочатку треба обчислити інтеграл
Права частина формули (1.6) є подвійним інтегралом по області Якщо область
Формула (1.7) зводить обчислення потрійного інтеграла до послідовного обчислення трьох визначених інтегралів. Порядок інтегрування у формулі (1.7) може бути й іншим, тобто змінні
Перехід до циліндричних координат у потрійному інтегралі Циліндричні і декартові координати пов’язані відношенням:
Потрійний інтеграл у циліндричних координатах має вигляд:
Перехід до сферичних координат у просторі Сферичні координати
А перехід від сферичних координат до декартових відбувається за формулою:
де область
Механіки і фізики Обчислення маси плоскої пластинки: Якщо пластинка лежить у площині
Якщо матеріальне тіло Обчислення статичних моментів: статичні моменти плоскої матеріальної пластинки визначаються за формулами:
Якщо тіло знаходиться у просторі
Координати центра маси: координати центра маси матеріальної пластини обчислюються за формулами:
У випадку трьохвимірного простору:
ІДЗ №1 1. Представити подвійний інтеграл Область D зображена на рисунку 1.1, обмежена лініями
Виразимо змінну
Знайдемо точки перетину ліній
Отже, маємо:
2. Обчислити подвійний інтеграл по області D, обмежений вказаними лініями: Область D зображена на рисунку 1.2.
Оскільки область D симетрична відносно вісі
3. Обчислити подвійний інтеграл, використовуючи полярні координати:
Область D зображена на рисунку 1.3.
Перейдемо до полярної системи координат:
Маємо:
4. Обчислити площу плоскої області D, обмеженої заданими лініями: Подана плоска фігура обмежена зверху параболою
Знайдемо точки перетину параболи із лінією:
Якщо Якщо Маємо точки перетину заданих ліній: (2;-6), (-2;-6). Оскільки область D симетрична відносно осі Оу, то маємо:
5. За допомогою подвійних інтегралів обчислити в полярних координатах площу плоскої фігури, обмеженої вказаними лініями: Перейдемо до полярної системи координат:
Рівняння лінії у полярних координатах має вигляд:
6. Обчислити об’єм тіла, обмеженого заданими поверхнями:
Дане тіло обмежено зверху площиною
ІДЗ №2 1. Розставити межі інтегрування у потрійному інтегралі Область інтегрування зображена на рисунках 2.1, 2.1а.
Рис. 2.1рис. 2.1а
2. Обчислити потрійний інтеграл:
Область
3. Обчислити потрійний інтеграл за допомогою циліндричних або сферичних координат: На рисунку 2.3 зображена область V та її проекція D на площину
Виконаємо деякі перетворення рівнянь Перейдемо до циліндричних координат
4. За допомогою потрійного інтеграла обчислити об’єм тіла, обмеженого вказаними лініями:
Рівняння
ІДЗ № 3 1. Обчислити масу неоднорідної пластинки D, обмеженої заданими лініями, якщо поверхнева густина в кожній точці Для обчислення маси Отже, маса пластинки:
2. Обчислити статичний момент однорідної пластини D, обмеженої вказаними лініями, відносно вказаної осі, використавши полярні координати:
Перейдемо до полярних координат:
Статичний момент відносно осі
3. Обчислити координати центра мас однорідного тіла, що займає область V, обмежену заданими поверхнями: Дане тіло (рис. 3.3 )симетричне відносно осі
Перейдемо до циліндричних координат за формулами:
Тоді одержуємо:
Отже, а центр маси має координати
Список літератури
1. Тевяшев А. Д., Литвин О. Г., Кривошеєва Г. М. та ін.. Вища математика у прикладах і задачах. Частина 2. – Харків: Фактор-Друк, 2002. 2. Ємець О. О., Недобачій С. І.. Методичні вказівки до виконання курсової роботи з дисципліни «Математичний аналіз» (2-ий курс, 3-ій семестр) для студентів спеціальностей «Прикладна математика», «Інформатика». – Полтава: ПолтНТУ, 2003. 3. Шкіль М. І.. Математичний аналіз: Підручник: у 2 ч. – 3-тє вид., переробл. і допов. – К.: Вища шк.., 2005. 4. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Том 3 5. Сборник индивидуальных задач по высшей математики: Учеб. Пособие. В 3 ч. Ч.3/Рябушко А. П., Бархатов В. В., Державцев В. В., Юруть И. Е.. – М.:Выс. Шк., 1991.
Поиск по сайту: |
 паралельно осі
паралельно осі  , перетинає границю області
, перетинає границю області 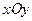 є правильною областю
є правильною областю 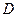 , то область
, то область 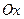 і
і  .
.
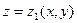 і
і  відповідно, а з боків циліндричною поверхнею, твірні якої паралельні
відповідно, а з боків циліндричною поверхнею, твірні якої паралельні 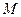 і
і 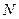 . Точку
. Точку  і
і  . Тоді
. Тоді  ,
,  і для будь-якої неперервної в області
і для будь-якої неперервної в області  має місце формула:
має місце формула: . (1.5)
. (1.5) по змінній
по змінній  , вважаючи, що змінні
, вважаючи, що змінні  і
і 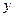 сталі. Інтеграл
сталі. Інтеграл  називають внутрішнім інтегралом, бо
називають внутрішнім інтегралом, бо . (1.6)
. (1.6) ,
,  , а
, а  , при чому
, при чому 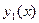 і
і  неперервні в області
неперервні в області  , то переходячи від подвійного інтеграла у формулі (1.6) до повторного, одержимо формулу:
, то переходячи від подвійного інтеграла у формулі (1.6) до повторного, одержимо формулу: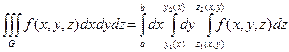 . (1.7)
. (1.7)
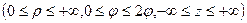 .
. ,
, - у полярній.
- у полярній. ,
,  і декартові координати пов’язані відношенням:
і декартові координати пов’язані відношенням:
 .
. ,
, , то маса
, то маса  пластинки обчислюється за формулою:
пластинки обчислюється за формулою: .
. , то маса тіла обчислюється за формулою:
, то маса тіла обчислюється за формулою:  .
. .
.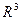 , то статичні моменти тіла
, то статичні моменти тіла  .
. .
.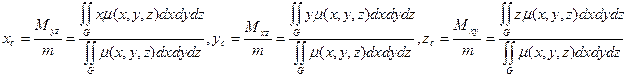
 у вигляді повторного інтеграла із зовнішнім інтегруванням по
у вигляді повторного інтеграла із зовнішнім інтегруванням по 
 ,
, 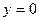 .
. Рис. 1.1
Рис. 1.1
 і
і  :
:

 - не задовольняє умову.
- не задовольняє умову. .
.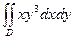

 Рис. 1.2
Рис. 1.2
 .
.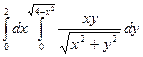 .
. Рис. 1.3
Рис. 1.3 ,
,  ,
,  .
.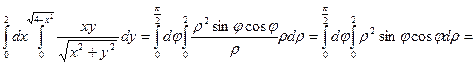
 .
.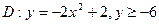 .
. , а знизу прямою
, а знизу прямою  (рис. 1.4).
(рис. 1.4). Рис. 1.4
Рис. 1.4
 , то
, то  , то
, то 
 .
. .
.
 Рис. 1.5
Рис. 1.5 . Оскільки лінія симетрична відносно осі Ox й Оу, то площа плоскої фігури дорівнює:
. Оскільки лінія симетрична відносно осі Ox й Оу, то площа плоскої фігури дорівнює:


 .
.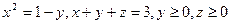 .
. Рис. 1.6
Рис. 1.6 (рис. 1.6), тому його об’єм визначаємо наступним чином:
(рис. 1.6), тому його об’єм визначаємо наступним чином:


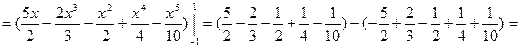
 .
. , якщо область V обмежена вказаними поверхнями. Накреслити область інтегруваня:
, якщо область V обмежена вказаними поверхнями. Накреслити область інтегруваня: .
.

 .
.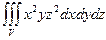
 .
. зображена на рис. 2.2.
зображена на рис. 2.2.  Рис. 2.2
Рис. 2.2
 .
. .
. .
. Рис. 2.3
Рис. 2.3 :
: 

 :
: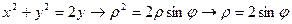 ;
; ;
;


 .
. .
. Рис. 2.4
Рис. 2.4 визначає зрізаний циліндр, інші поверхні є площинами (рис. 2.4). Отже, маємо:
визначає зрізаний циліндр, інші поверхні є площинами (рис. 2.4). Отже, маємо:
 .
. .
. скористаємось фізичним змістом подвійного інтеграла і формулою
скористаємось фізичним змістом подвійного інтеграла і формулою  , де область інтегрування зображена на рисунку 3.1.
, де область інтегрування зображена на рисунку 3.1.
 .
. Рис. 3.1
Рис. 3.1 .
. Рис. 3.2
Рис. 3.2

 . У полярній системі координат область D (рис. 3.2) перетворюється на область
. У полярній системі координат область D (рис. 3.2) перетворюється на область  . Отже, маємо:
. Отже, маємо:

 .
. .
. ,
,  .
.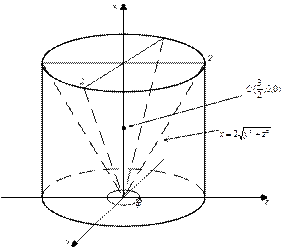 Рис. 3.3
Рис. 3.3


 ,
,