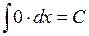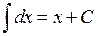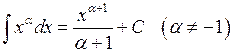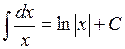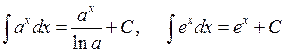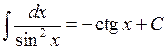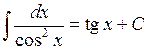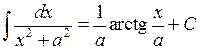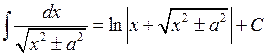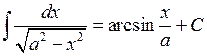|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поняття первісної і невизначеного інтегралаСтр 1 из 5Следующая ⇒
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ Конспект лекцій по курсу вищої математики для студентів I курсу ГГФ (спец. географія)
Одеса, 2009
Поняття первісної і невизначеного інтеграла. В розділі «Диференціальне числення функцій однієї змінної» ми познайомилися з одним з фундаментальних понять математичного аналізу – поняттям похідної:
За даною функцією ми знаходимо її похідну. В багатьох питаннях науки необхідно розв’язувати обернену задачу: за даною похідною З механічної точки зору це можна інтерпретувати, наприклад, так: за миттєвою швидкістю З’ясовується, що ця задача набагато складніша, ніж задача диференціювання. Більш того, якщо обмежуватись лише елементарними функціями, то вона взагалі може не мати розв’язків. Наприклад, серед елементарних функцій не існує такої, похідна якої дорівнює Перейдемо до точних означень. Означення.Функція Приклади: 1. Нехай 2. Нехай Помітимо, що для функції
Теорема.Якщо функція Доведеннядуже просте. Дійсно:
Таким чином, задача знаходження первісної розв’язується неоднозначно. Додаючи до будь якої первісної функції Теорема.Нехай
Доведення.Позначимо
Візьмемо два довільні значення
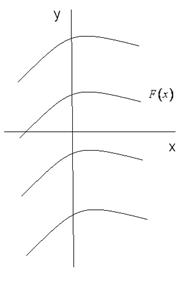
З цих двох теорем випливає, що якщо функція Геометрично цей факт ілюструється так (рис. 1.1): графік будь якої первісної функції
Рис.1.1
Означення.Сукупність всіх первісних функції
При цьому функція Символ З означення невизначеного інтеграла фактично випливає і формула для його обчислення:
Тобто до будь якої первісної На підставі розглянутих вище прикладів, зокрема, випливає:
Сформулюємо деякі властивості невизначеного інтеграла: 1.Похідна від невизначеного інтеграла дорівнює підінтегральній функції: 2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:
3. Невизначений інтеграл від диференціала деякої функції дорівнює цій функції плюс довільна стала:
Властивості 1 – 3 по-різному висловлюють той факт, що операція інтегрування є оберненою до операції диференціювання.
4. Сталий множник можна виносити за знак невизначеного інтеграла:
5. Невизначений інтеграл від суми (різниці) двох функції дорівнює сумі (різниці) невизначених інтегралів від цих функцій:
Властивості 4,5 є наслідками відповідних властивостей похідних.
Таблиця інтегралів основних елементарних функцій. На підставі означення невизначеного інтеграла і таблиці похідних (див. розділ «Диференціальне числення функцій однієї змінної») можна написати відповідну таблицю інтегралів. Щоправда, у цій таблиці будуть міститись деякі формули, які не відображаються таблицею похідних. Ці формули перевіряються безпосереднім диференціюванням. Отже:
Поиск по сайту: |
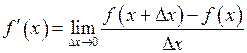 .
. знайти функцію
знайти функцію  .
. матеріальної точки в момент часу
матеріальної точки в момент часу  встановити координату
встановити координату 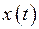 точки в цей момент часу.
точки в цей момент часу.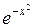 .
.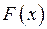 називається первісною для функції
називається первісною для функції  , якщо
, якщо 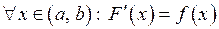 .
. . Тоді
. Тоді  . Дійсно,
. Дійсно, 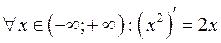 .
. . Тоді
. Тоді  . Дійсно,
. Дійсно,  .
. первісними будуть також функції
первісними будуть також функції 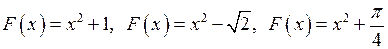 , і взагалі будь яка функція вигляду
, і взагалі будь яка функція вигляду 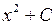 , де
, де  – стала. Відповідно для функції
– стала. Відповідно для функції 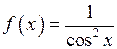 первісними будуть всі функції вигляду
первісними будуть всі функції вигляду  . Узагальнимо цей факт у вигляді наступної теореми:
. Узагальнимо цей факт у вигляді наступної теореми: є первісною для функції
є первісною для функції 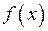 на інтервалі
на інтервалі 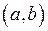 , то будь яка функція вигляду
, то будь яка функція вигляду 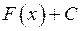 , де
, де  .
. і
і 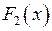 – будь які первісні функції
– будь які первісні функції  справджується рівність:
справджується рівність: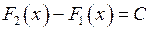 .
.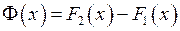 . Тоді
. Тоді  .
.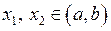 такі, що
такі, що 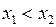 і розглянемо різницю
і розглянемо різницю 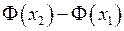 . Згідно з теоремою Лагранжа (див. п. 6.6) на інтервалі
. Згідно з теоремою Лагранжа (див. п. 6.6) на інтервалі 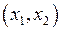 існує така точка
існує така точка 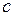 , що буде виконана рівність:
, що буде виконана рівність: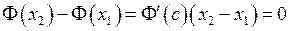 (оскільки
(оскільки 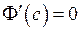 ). Отже
). Отже  , тобто значення функції
, тобто значення функції 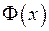 співпадають в двох довільних точках інтервалу
співпадають в двох довільних точках інтервалу 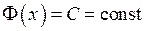 на
на 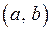 , що й треба було довести.
, що й треба було довести. .
.
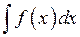 .
.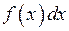 підінтегральним виразом.
підінтегральним виразом.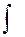 був введений Лейбніцем у 1686 році. Цей символ є дещо деформована латинська буква S – перша буква слова Summa. Термін «інтеграл» (від латинського integer – цілий)був запропонований у 1696 році Йоганном Бернуллі. В приведеному означенні мається на увазі збирання в одне ціле всіх первісних даної функції.
був введений Лейбніцем у 1686 році. Цей символ є дещо деформована латинська буква S – перша буква слова Summa. Термін «інтеграл» (від латинського integer – цілий)був запропонований у 1696 році Йоганном Бернуллі. В приведеному означенні мається на увазі збирання в одне ціле всіх первісних даної функції.
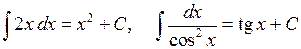 .
.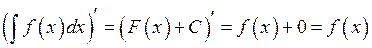 .
.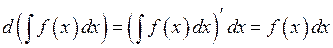 .
.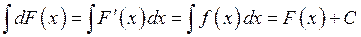 .
.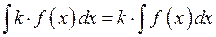 .
.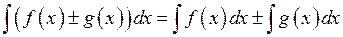 .
.